Interval spolehlivosti pro koeficient korelace

V praxi bývá velice užitečný také interval spolehlivosti pro koeficient korelace, který nám poskytuje názornou představu o závislosti dvou normálně rozdělených náhodných veličin.

Věta 4.12. Jestliže dvourozměrný náhodný výběr rozsahu pochází z dvourozměrného normálního rozložení, jehož koeficient korelace se příliš neliší od nuly a rozsah výběru je dostatečně velký lze odvodit, že  interval spolehlivosti pro má meze

Nejsou-li uvedené podmínky splněny, pak nelze tento vzorec použít, protože rozložení výběrového korelačního koeficientu je příliš zešikmené. V takovém případě využijeme následujícího tvrzení.

Věta 3.13. Náhodná veličina

má i při malém rozsahu výběru přibližně normální rozložení se střední hodnotou

(2. sčítanec lze při větším zanedbat) a rozptylem

Standardizací veličiny dostaneme veličinu

která má asymptoticky rozložení

Tudíž  asymptotický interval spolehlivosti pro  bude mít meze Interval spolehlivosti pro  pak dostaneme zpětnou transformací.

Poznámka 4.14. Jelikož dostáváme a meze intervalu spolehlivosti pro  můžeme psát ve tvaru

Příklad 4.15. Pracovník personálního oddělení určité firmy zkoumá, zda existuje vztah mezi počtem dní absence za rok (veličina ) a věkem pracovníka (veličina ). Proto náhodně vybral údaje o 10 pracovnících.

Za předpokladu, že uvedené údaje tvoří číselné realizace náhodného výběru rozsahu 10 z dvourozměrného normálního rozložení, vypočtěte výběrový koeficient korelace a na hladině významnosti 0,05 testujte hypotézu, že a jsou nezávislé náhodné veličiny. Sestrojte 95% asymptotický interval spolehlivosti pro skutečný koeficient korelace 

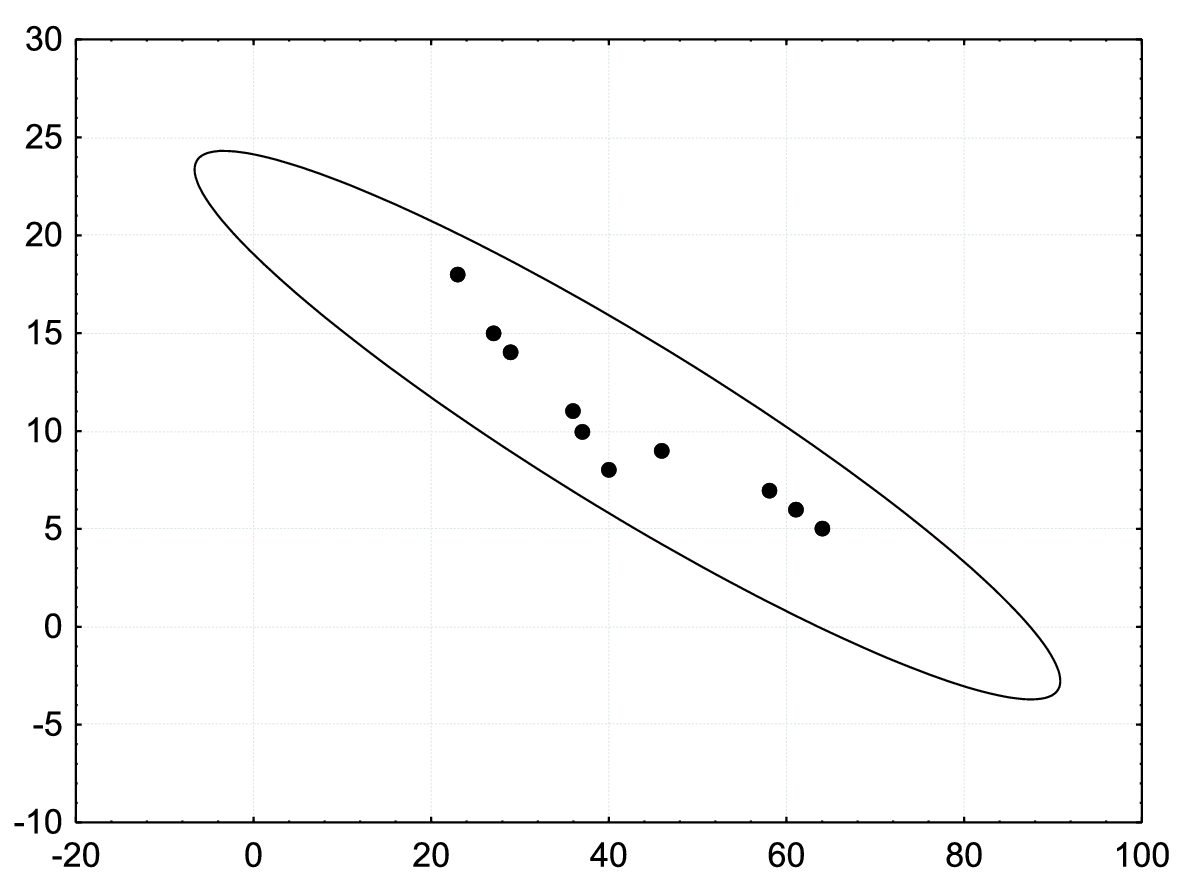
Řešení. Předpoklad o dvourozměrné normalitě dat ověříme orientačně pomocí dvourozměrného tečkového diagramu:

Obr. 2. Dvourozměrný tečkový diagram

Vzhled diagramu svědčí o tom, že předpoklad je oprávněný.

Testujeme proti Vypočítáme tedy mezi věkem pracovníka a počtem dnů pracovní neschopnosti existuje silná nepřímá lineární závislost. Testová statistika: kvantil kritický obor

Jelikož zamítáme na hladině významnosti 0,05 hypotézu o nezávislosti veličin a Vypočítáme

Meze 95% asymptotického intervalu spolehlivosti pro  jsou tedy s pravděpodobností přibližně 0,95.