Optimální volba predikční funkce g

Pomocí regresní a korelační analýzy lze provádět predikce nejrůznějšího typu. Nejzávažnější otázkou je, jak volit vhodnou predikční funkci .

Věta 2.1. Nechť  jsou náhodné veličiny. Označme  a nechť  Pak pro každou měřitelnou funkci

platí

a rovnost v uvedené nerovnosti nastává právě když

Poznámka 2.2. (Podmíněná střední hodnota). V předchozí větě se vyskytl nový výraz  pro tzv. podmíněnou střední hodnotu. Nebudeme uvádět přesnou definici, pro jednoduchost vysvětlíme tento pojem pro spojité náhodné veličiny a :

Nechť spojitý náhodný vektor  má sdruženou distribuční funkci a dále nechť náhodné veličiny a mají marginální hustoty , resp. . Označme

nazveme podmíněnou střední hodnotou náhodné veličiny při daném . Dá se ukázat, že jsou splněny např. tyto vlastnosti:

• Nechť  jsou náhodné veličiny a  jsou reálné konstanty, pak pokud střední hodnoty  existují, platí 

(1)

• Nechť  jsou náhodné veličiny a střední hodnota  existuje, pak

(2)

Definujeme také podmíněný rozptyl náhodné veličiny při daném vztahem

Poznámka 2.3. (Korelační koeficient). Připomeňme ještě tzv. Pearsonův¹ koeficient korelace náhodných veličin  (které jsou aspoň intervalového charakteru). Ten je definován vztahem

kde  je kovariance náhodných veličin a .

• 
• 
• 
•   a rovnosti je dosaženo tehdy a jen tehdy, když existují reálné konstanty , kde  tak, že   přičemž  pro  a   pro .

Z těchto vlastností plyne, že  je vhodnou mírou těsnosti lineárního vztahu náhodných veličin .

Věta 2.4. Mějme náhodnou veličinu s konečným a nenulovým rozptylem a náhodný vektor . Potom
pro libovolnou měřitelnou funkci

takovou, že existuje korelační koeficient  platí 

rovnost nastává v případě, že  právě když  je lineární funkcí  skoro všude vzhledem k  V případě, že nastává rovnost při libovolné volbě funkce .

Výsledky uvedené v předchozích dvou větách ukazují velký význam podmíněné střední hodnoty v regresní a korelační analýze.

(1)	Z první věty plyne, že nejlepší predikci náhodné veličiny  pomocí náhodných veličin , která minimalizuje střední kvadratickou chybu , dostaneme, když položíme V této souvislosti potom nejlepší prediktor  nazýváme regresní funkcí náhodné veličiny na náhodných veličinách
(2)	Z druhé věty plyne, že regresní funkce  je prediktor, který má ze všech možných prediktorů  největší korelační koeficient s predikovanou náhodnou veličinou . To znamená, že regresní funkce  je optimálním prediktorem v tom smyslu, že má maximální statistickou vazbu (měřenou korelačním koeficientem) s predikovanou náhodnou veličinou .

Definice 2.5. Mějme náhodnou veličinu s konečným a nenulovým rozptylem a náhodný vektor . Potom číslo

nazýváme korelačním poměrem náhodné veličiny  na náhodném vektoru , nebo též korelačním poměrem náhodné veličiny  na náhodných veličinách  a pak jej též značíme

(1)	Z předchozích vět plyne, že a tedy pro korelační poměr platí nerovnost
(2)	Po vydělení rovnosti (14) rozptylem a jednoduché úpravě dostaneme Označme symbolem  střední kvadratickou chybu predikce, když prediktorem je regresní funkce , tj. pak díky předchozímu máme Z tohoto vztahu plyne velice názorná interpretace korelačním poměru
	(a)	Je-li střední kvadratická chyba predikce   tedy v případě ideální predikce, je korelační poměr
	(b)	V druhém krajním případě, když střední kvadratická chyba predikce je rovna , tj.  pak je  a yužití informace, kterou o náhodné veličině poskytuje náhodný vektor , nepřináší žádné zmenšení chyby predikce.

 

Tedy korelační poměr  poskytuje míru přesnosti predikce a je velice užitečný při srovnávání různých vektorů doprovodných proměnných.

 

Poznámka 2.7. (polopatě). Vysvětleme si předchozí pojmy pomocí následujícího obrázku.

Na obrázku je symbolicky znázorněn případ, kdy se zkoumá závislost mezi náhodnými veličinami  a . I když jsou vykresleny již konkrétní realizace náhodných veličin (plné kroužky), značení je provedeno velkými písmeny, aby bylo lépe rozumět předchozím vztahům. Přímka představuje predikci v tomto modelu a prázdné kroužky příslušné predikované hodnoty. Symbol označuje celkovou variabilitu náhodné veličiny , tj. odchylku od své střední hodnoty (umocněnou na druhou). Symbol  představuje variabilitu vysvětlenou modelem, tj. odchylku predikovaných hodnot od střední hodnoty Podíl těchto odchylek (umocněných na druhou) definuje korelační poměr  Symbol  odpovídá tzv. reziduální variabilitě, tj. odchylce náhodné veličiny od své predikce.

Návod 2.8. Při praktických výpočtech se příslušné rozptyly odhadují výběrovými rozptyly. Odhadnutý korelační poměr  se pak nazývá index determinace.Nechť tedy máme realizace  a jejich predikované hodnoty Koeficient determinace má tvar

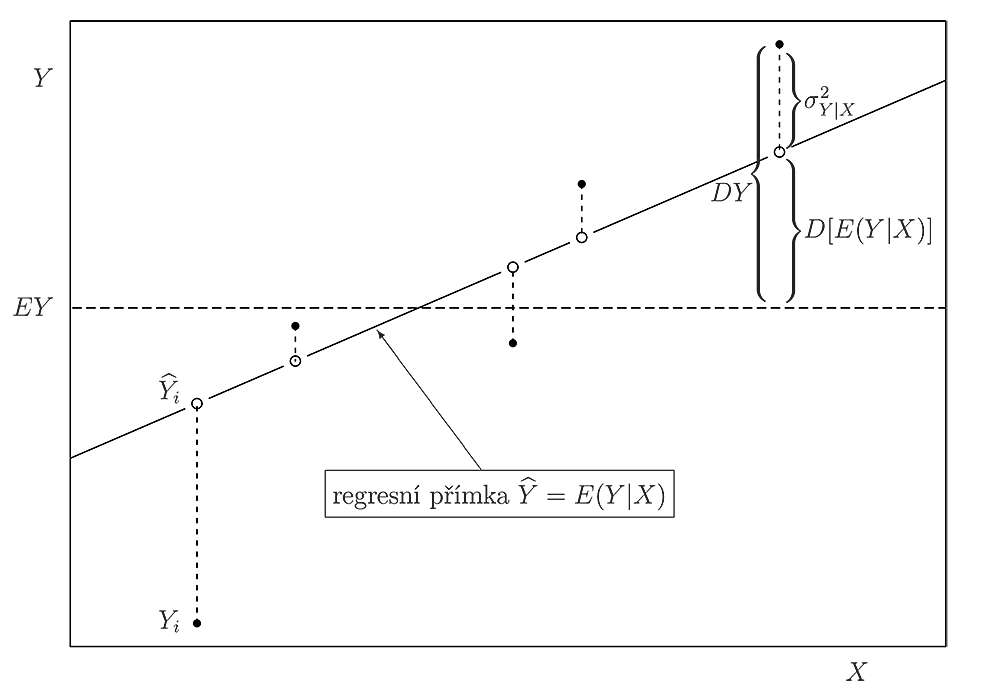
Příklad 2.9. Při laboratorním pokusu bylo získáno následujících 8 výsledků měření

 

Zvolený model nám predikoval tyto hodnoty

Určete index determinace a interpretujte ho.

 

Řešení. Ukážeme oba způsoby výpočtu. Vypočteme nejprve příslušné výběrové rozptyly:

Podle definice je

nebo

Výsledek lze interpretovat tak, že celkové variability je vysvětleno zvoleným modelem. 

¹ Karl Pearson (1857 - 1936). Britský statistik a matematik. Studoval na Cambridge a poté působil na univerzitě v Londýně. Vychoval řadu vynikajících statistiků.