Modely pro poissonovská data

Celočíselná data lze modelovat pomocí diskrétních rozdělení. V předchozí sekci jsme se zabývali alternativními a binomickými daty. Nyní soustřeďme pozornost na poissonovská data.

Předpokládejme, že náhodný výběr rozsahu je z Poissonova rozdělení, tj.

přičemž

Poznámka 3.1. Dále se tímto rozdělením řídí náhodná veličina, kterou je počet výskytu sledovaného jevu v určitém časovém intervalu délky  (nebo počet výskytu sledovaného jevu na ploše velikosti apod.).

Jestliže jsou  splněny následující podmínky

a)	jev může nastat v kterémkoliv časovém okamžiku,
b)	počet výskytů jevu během časového intervalu závisí jen na jeho délce a ne na jeho počátku ani na tom, kolikrát jev nastoupil před jeho počátkem,
c)	pravděpodobnost, že jev nastoupí více než jednou v intervalu délky konverguje k nule rychleji než
d)	je střední hodnota počtu výskytů jevu za časovou jednotku

pak uvedená náhodná veličina má rozdělení

Náhodnou veličinou, která má Poissonovo rozdělení, je tedy např.

• počet vadných výrobků ve velké sérii, jestliže pravděpodobnost vyrobení vadného výrobku je velmi malá,
• počet těžkých dopravních úrazů za den v určitém městě,
• počet zákazníků v prodejně během nějakého časového intervalu,
• počet částic v jednotce plochy nebo objemu, např. počet částic v zorném poli mikroskopu,
• počet telefonních volání v časovém intervalu 
• počet létavic pozorovaných během intervalu délky

Předpokládejme opět, že náhodná veličina závisí na veličinách  (tzv. kovariáty) a úkolem bude najít vztah mezi nimi, tj. hledáme funkci

Protože chceme použít GLM modely, modelujeme pravděpodobnosti pomocí linkovacích funkcí

Definice 3.2. Pokud v modelu uvažujeme identickou linkovací funkci, tj. platí

mluvíme o lineárním modelu.

Avšak tento model má řadu nevýhod, především je třeba zajistit, aby nabývala pouze kladných hodnot, nejčastěji se proto volí následující dvě možnosti:

Definice 3.3. Pokud v modelu předpokládáme vztah

tj. uvažujeme linkovací funkci

hovoříme o log-lineárním modelu.

Definice 3.4. Pokud v modelu předpokládáme vztah

tj. uvažujeme linkovací funkci

hovoříme o odmocninovém modelu (square-root-linear model).

Příklad. V souboru „aids.RData“ jsou uvedeny údaje o počtech nových případů AIDS ve Velké Británii za období prosinec 1982 až listopad 1985. Datový soubor obsahuje tyto proměnné

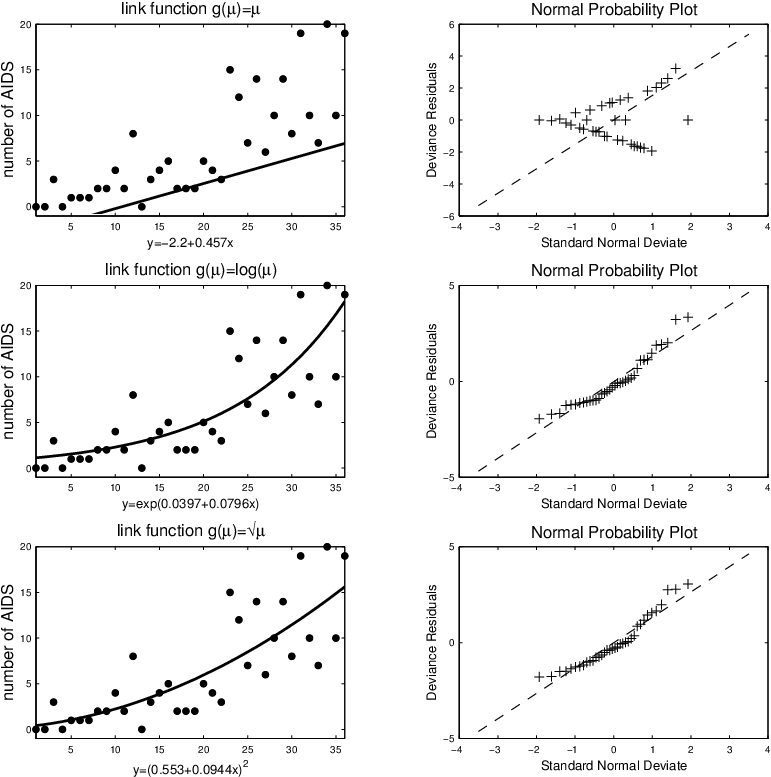
Řešení. Pro modelování závislosti použijeme lineární model, log-lineární model a odmocninový model. Výsledky jsou znázorněny na následujícím obrázku.

Obr. 8. Modely pro výskyt nových onemocnění AIDS ve Velké Británii.