Normal probability plot (N-P plot)

Umožňuje graficky posoudit, zda data pocházejí z normálního rozložení.

 

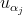Způsob konstrukce 4.4. N-P plot konstruujeme tak, že na vodorovnou osu vynášíme uspořádané hodnoty  a na svislou osu kvantily normálního rozdělení , kde

Poznámka 4.5. Jsou-li některé hodnoty  stejné,  pak za j bereme průměrné pořadí odpovídající takové skupince.

Poznámka 4.6.

• Pocházejí-li data z normálního rozložení, pak budou všechny dvojice   ležet na přímce.
• Pro data z rozložení s kladnou šikmostí se budou dvojice řadit do konkávní křivky.
• Pro data z rozložení se zápornou šikmostí se budou dvojice  řadit do konvexní křivky.

Příklady N-P plotu pro jednotlivé případy jsou v části Vzhled diagnostických grafů pro rozložení s různou šikmostí.