Metody mnohonásobného porovnávání

Zamítneme-li na hladině významnosti  hypotézu o shodě středních hodnot, chceme zjistit, které dvojice středních hodnot se liší na dané hladině významnosti . Mají-li všechny výběry týž rozsah  (říkáme, že třídění je vyvážené), použijeme Tukeyovu¹ metodu, nemají-li všechny výběry stejný rozsah, použijeme Scheffého² metodu.

Věta 4.1. (Tukeyova metoda). Rovnost středních hodnot  a  zamítneme na hladině významnosti , když:

kde  jsou kvantily studentizovaného rozpětí, které najdeme ve statistických tabulkách.

Věta 4.2. Rovnost středních hodnot  a  zamítneme na hladině významnosti , když:

Poznámka 4.3. Může nastat situace, kdy při zamítnutí nulové hypotézy nenajdeme významný rozdíl u žádné dvojice středních hodnot. Pak je významně rozdílná některá složitější kombinace středních hodnot.

Příklad 4.4. U čtyř odrůd brambor (označených symboly A, B, C, D) se zjišťovala celková hmotnost brambor vyrostlých vždy z jednoho trsu. Výsledky uvádí tabulka:

Na hladině významnosti 0,05 testujte hypotézu, že střední hodnota hmotnosti trsu brambor nezávisí na odrůdě. Zamítnete-li nulovou hypotézu, zjistěte, které dvojice odrůd se liší na hladině významnosti 0,05.

Řešení. Data považujeme za realizace čtyř nezávislých náhodných výběrů ze čtyř normálních rozložení se stejným rozptylem. Testujeme hypotézu, že všechny čtyři střední hodnoty jsou stejné.
Výpočtem získáme:

Ze statistických tabulek získáme  

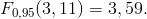
Protože testová statistika se realizuje v kritickém oboru, zamítáme nulovou hypotézu na hladině významnosti 0,05.
Výsledky zapíšeme do tabulky ANOVA:

Nyní pomocí Scheffého metody zjistíme, které dvojice odrůd se liší na hladině významnosti 0,05.

Na hladině významnosti 0,05 se liší odrůdy A a C.

 

Poznámka 4.5. Význam předpokladů v analýze rozptylu

• Nezávislost jednotlivých náhodných výběrů - velmi důležitý předpoklad, musí být splněn, jinak dostaneme nesmyslné výsledky.
• Normalita - ANOVA není příliš citlivá na porušení normality, zvlášť pokud mají všechny výběry rozsah nad 20 (důsledek centrální limitní věty). Při výraznějším porušení se doporučuje Kruskalův - Wallisův test (viz např. [3]).
• Shoda rozptylů - mírné porušení nevadí, při větším se doporučuje Kruskalův - Wallisův test. Test shody rozptylů má smysl provádět až po ověření předpokladu normality.

¹John Wilder Tukey (1915 - 2000). Americký matematik.

²Henry Scheffé (1907 - 1977). Americký matematik.