Testy dobré shody

I když uvádíme test dobré shody v souvislosti s testováním normality dat, uvedeme obecnou formulaci testů dobré shody, neboť mají široké využití v mnoha dalších partiích statistitky.

Věta 2.4. Testujeme hypotézu, která tvrdí, že náhodný výběr pochází z rozložení s distribuční funkcí

1. Je-li distribuční funkce spojitá, pak data rozdělíme do třídicích intervalů Zjistíme absolutní četnost -tého třídicího intervalu a vypočteme pravděpodobnost že náhodná veličina s distribuční funkcí se bude realizovat v -tém třídicím intervalu. Platí-li nulová hypotéza, pak
2. Má-li distribuční funkce nejvýše spočetně mnoho bodů nespojitosti, pak místo třídicích intervalů použijeme varianty Pro variantu zjistíme absolutní četnost a vypočteme pravděpodobnost že náhodná veličina s distribuční funkcí se bude realizovat variantou Platí-li nulová hypotéza, pak

(2)

Testová statistika:

(3)

Platí-li nulová hypotéza, pak kde je počet odhadovaných parametrů daného rozložení. (Např. pro normální rozložení protože z dat odhadujeme střední hodnotu a rozptyl.) Nulovou hypotézu zamítáme na asymptotické hladině významnosti když Aproximace se považuje za vyhovující, když

Poznámka 2.5. Hodnota testové statistiky je silně závislá na volbě třídicích intervalů. Navíc při nesplnění podmínky je třeba některé intervaly resp. varianty slučovat, což vede ke ztrátě informace.

Příklad 2.6. Byl zjišťován počet poruch určitého zařízení za 100 hodin provozu ve 150 disjunktních 100 h intervalech. Výsledky měření:

Na asymptotické hladině významnosti 0,05 testujte hypotézu, že náhodný výběr pochází z rozložení

Řešení. Pravděpodobnost, že náhodná veličina s rozložením kde bude nabývat hodnot a víc je 
Výpočty potřebné pro stanovení testové statistiky uspořádáme do tabulky.

  Protože nulovou hypotézu nezamítáme na asymptotické hladině významnosti 0,05.

Poznámka 2.7. Test dobré shody může být použit i v těch případech, kdy rozložení, z něhož daný náhodný výběr pochází, neodpovídá nějakému známému rozložení (např. exponenciálnímu, normálnímu, Poissonovu, ...), ale je určeno intuitivně nebo na základě zkušenosti.

Příklad 2.8. Ve svých pokusech pozoroval J.G. Mendel 10 rostlin hrachu a na každé z nich počet žlutých a zelených semen. Výsledky pokusu:

Z genetických modelů vyplývá, že pravděpodobnost výskytu žlutého semene by měla být 0,75 a zeleného 0,25. Na asymptotické hladině významnosti 0,05 testujte hypotézu, že výsledky Mendelových pokusů se shodují s modelem.

Řešení. Výpočty potřebné pro stanovení testové statistiky uspořádáme do tabulky.

Protože nulovou hypotézu nezamítáme na asymptotické hladině významnosti 0,05.

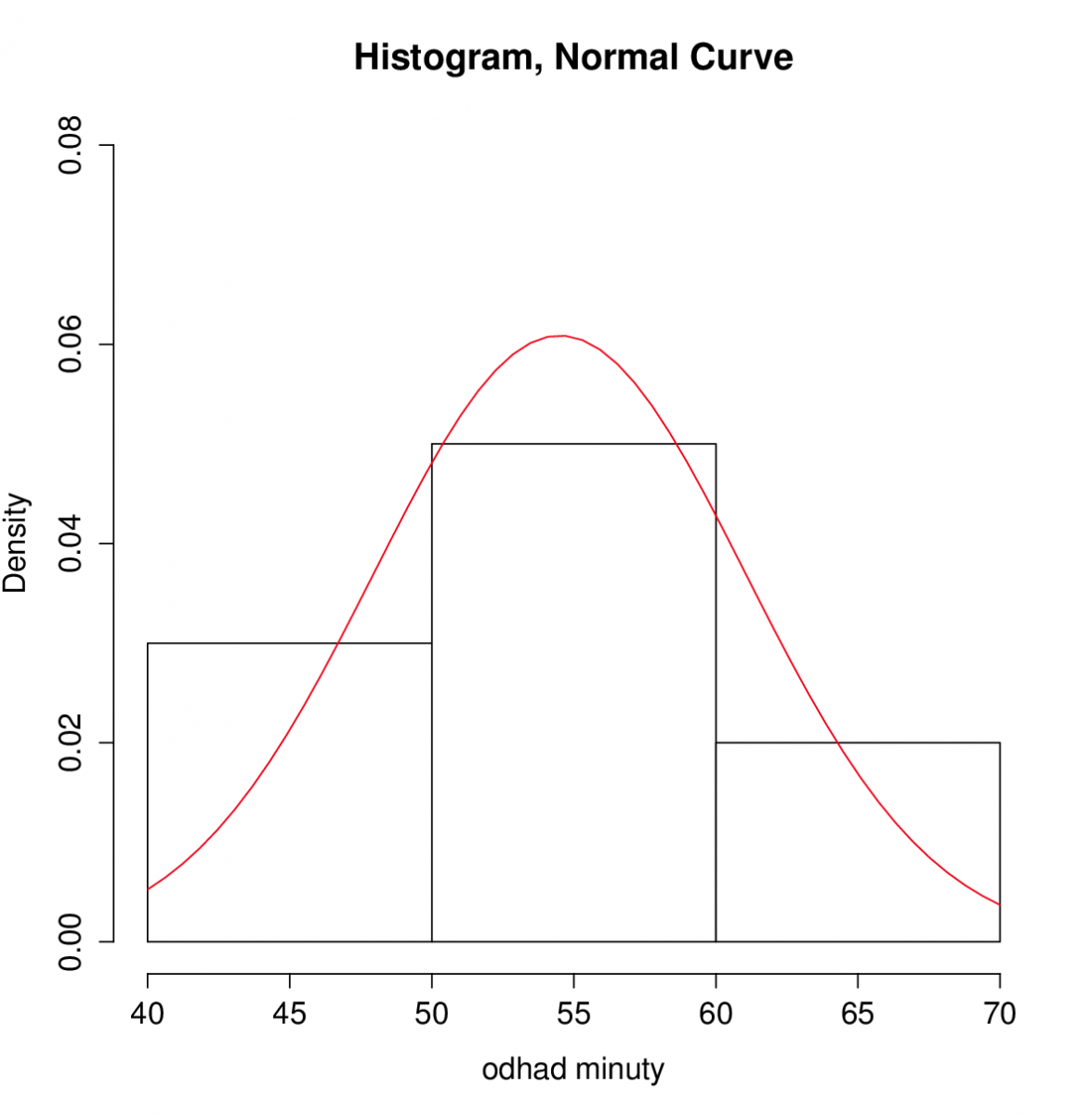
Příklad 2.9. Deset pokusných osob mělo nezávisle na sobě bez předchozího nácviku odhadnout, kdy od daného signálu uplyne jedna minuta. Výsledky pokusu jsou uvedeny v následující tabulce

Testujte graficky i výpočtem, zda se jedná o výběr z normálního rozdělení.

Řešení. Nejprve data rozdělíme do 3 třídících intervalů a vykreslíme histogram a křivku normální hustoty.

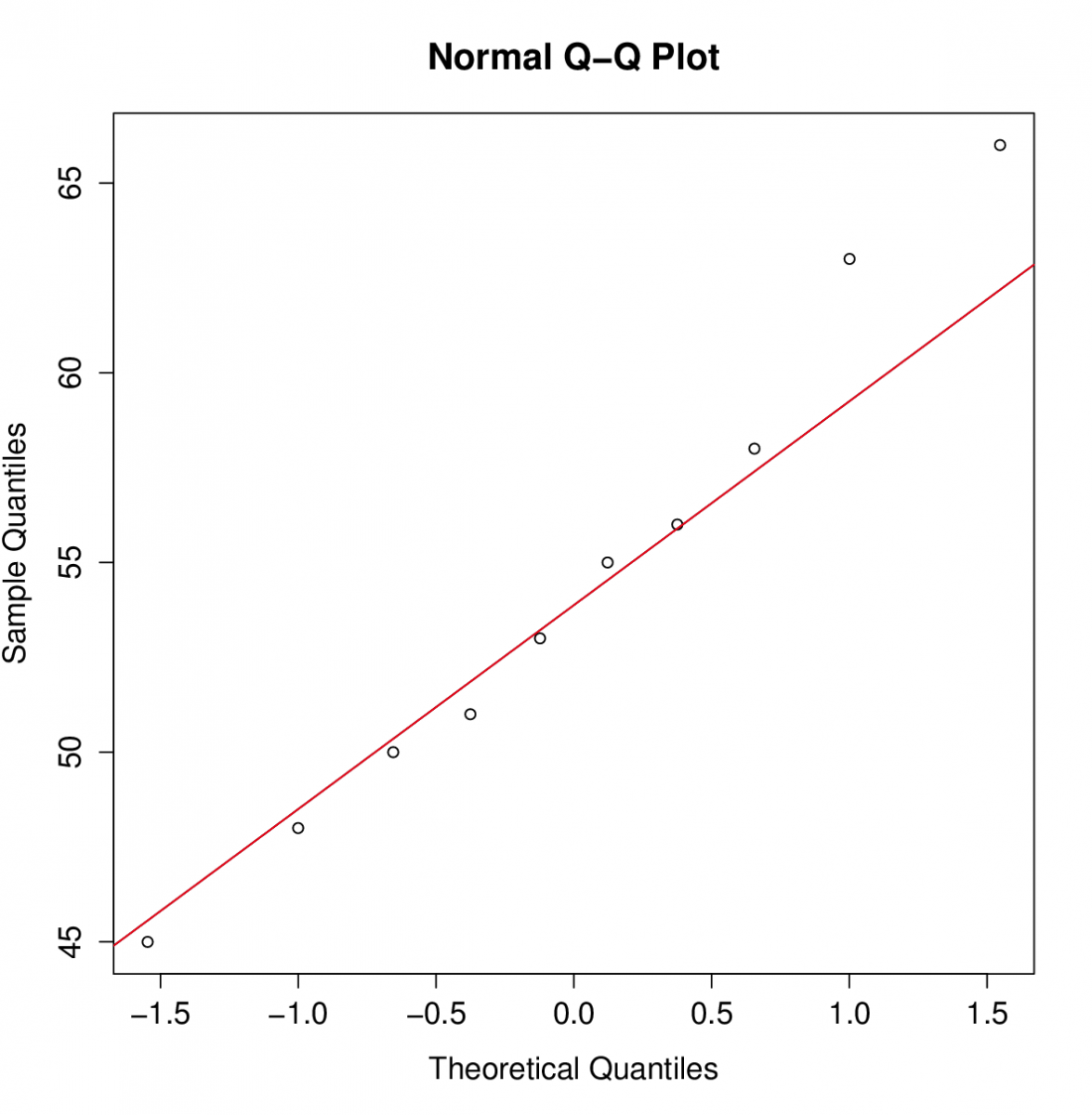
Z obrázku je vidět, že by data mohla pocházet z normálního rozdělení. Vykreslíme také Q-Q plot.

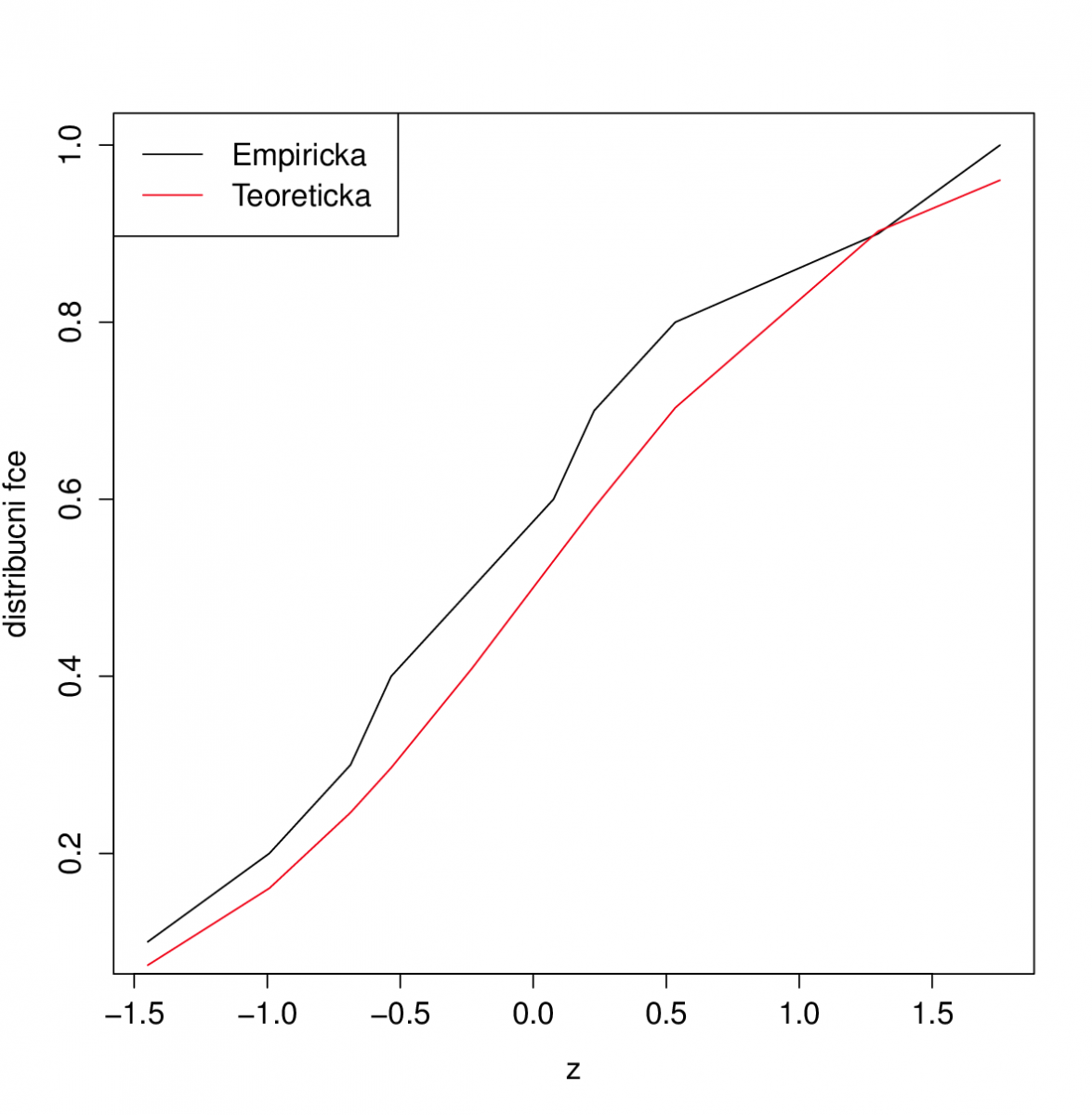
I z tohoto obrázku to vypadá na normální rozdělení. Nakonec ještě porovnáme graf výběrové distribuční funkce s grafem distribuční funkce normálního rozdělení.

Také tento obrázek ukazuje na normalitu dat. Závěrem ještě provedeme výše uvedené testy. Všechny přijímají hypotézu o tom, že data pocházejí z normálního rozdělení. Jejich -hodnoty jsou shrnuty v následující tabulce: