Odstranění autokorelace 1. řádu
V některých případech nás nezajímají pouze nezkreslené odhady ale chceme odstranit autokorelaci z dat nějakou vhodnou transformací. To je samozřejmě možné, je třeba si však uvědomit, že pak dostáváme úplně jiný model a následná interpretace výsledků je obtížně proveditelná.
Uveďme postup pro odstranění autokorelace 1. řádu:
- Jednou z dříve uvedených metod nalezneme odhad
- Vytvoříme nový model
tj. vznikne model
ve kterém již není přítomna autokorelace 1. řádu.
- Hledáme odhady
standardním způsobem.
Příklad 3.3. V letech 1953 - 1983 byly měřeny ztráty vody při distribuci do domácností. Výsledky měření jsou uloženy v souboru „voda.RData“. Proměnná
označuje množství vyrobené vody, proměnná
ztrátu. Ověřte, zda se v datech vyskytuje autokorelace 1. řádu a případně ji odstraňte.
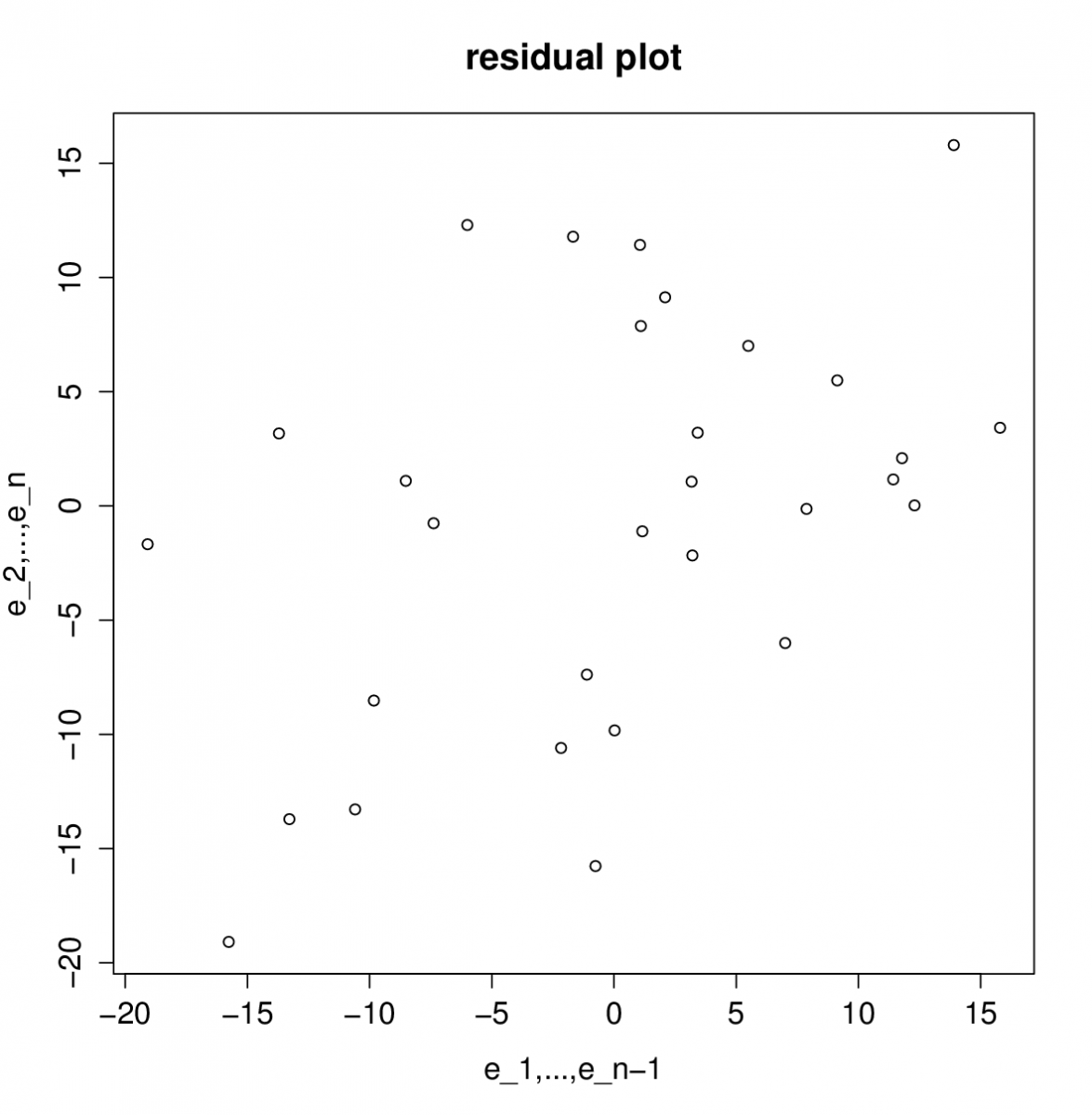
Řešení. Nejprve do grafu postupně vykreslíme hodnoty
v závislosti na

Z grafu je patrná lineární závislost a tudíž přítomnost autokorelace 1. řádu. Provedeme také oba testy na hladině významnosti
- Pro asymptotický test vychází hodnota testové statistiky
Nulovou hypotézu tedy zamítáme, neboť
- Pro Durbinův - Watsonův test máme
a
-hodnota testu je
takže také zamítáme nulovou hypotézu.
Nyní se pokusíme vhodnou transformací autokorelaci odstranit. Nejprve je třeba odhadnout parametr
Použijeme k tomu obě zmíněné metody. Odhady
jsou velmi podobné. Metodou nejmenších čtverců dostáváme odhad
Odhad pomocí Durbin - Watsonovy statistiky vychází
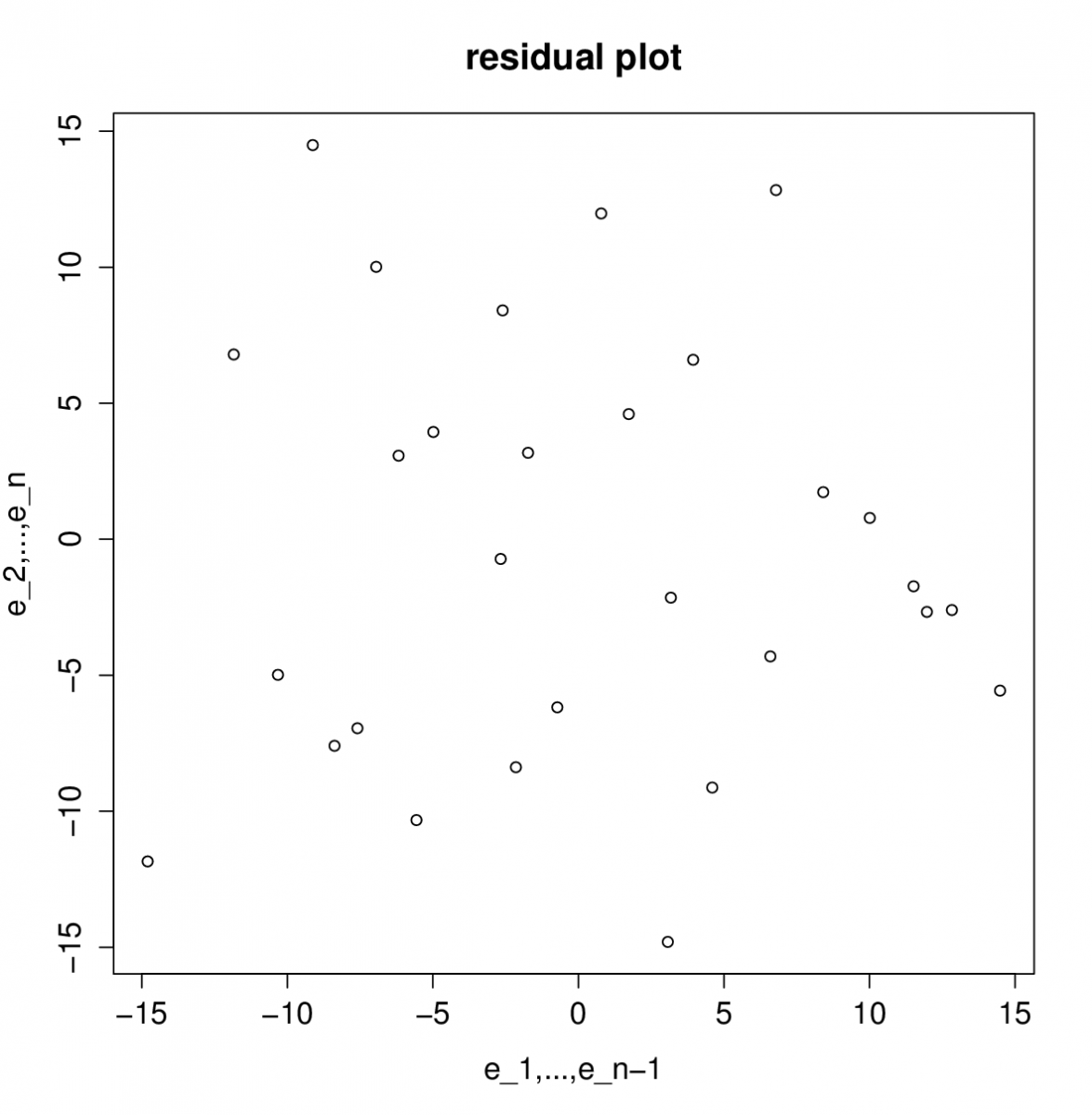
Pomocí tohoto odhadu vytvoříme nový model a v něm vykreslíme residua.
Z obrázku je patrná nezávislost residuí. Také Durbinův - Watsonův test již nezamítá nulovou hypotézu (jeho
-hodnota vychází
).