Koeficient korelace dvourozměrného normálního rozdělení

Připomeňme si základní vlastnosti dvourozměrného normálního rozdělení. Ty jsou popsány v následujících tvrzeních.

Věta 4.3. Nechť náhodný vektor má dvourozměrné normální rozložení s hustotou

přičemž

Pak marginální hustoty jsou:

Věta 4.4. Je-li pak pro tedy náhodné veličiny jsou stochasticky nezávislé. Jinými slovy: stochastická nezávislost složek  normálně rozloženého náhodného vektoru je ekvivalentní jejich nekorelovanosti.

Definice 4.5. Je-li jsou náhodné veličiny  stochasticky závislé. Je-li říkáme, že jsou kladně korelované, je-li říkáme, že jsou záporně korelované.

V dalším textu budeme předpokládat, že náhodný výběr pochází z dvourozměrného normálního rozdělení s parametry Využitím tohoto předpokladu dostáváme návod, jak testovat nezávislost dvou náhodných veličin pomocí výběrového koeficientu korelace.

Věta 4.6. Testujeme proti oboustranné alternativě  (resp. proti levostranné alternativě resp. proti pravostranné alternativě ). Testová statistika má tvar:

Platí-li nulová hypotéza, pak

Kritický obor pro test proti oboustranné alternativě:

proti levostranné alternativě:

a proti pravostranné alternativě:

zamítáme na hladině významnosti když

Příklad 4.7. Máme k dispozici výsledky testů ze dvou předmětů zjištěné u osmi náhodně vybraných studentů určitého oboru.

Na hladině významnosti 0,05 testujte hypotézu, že výsledky obou testů nejsou kladně korelované.

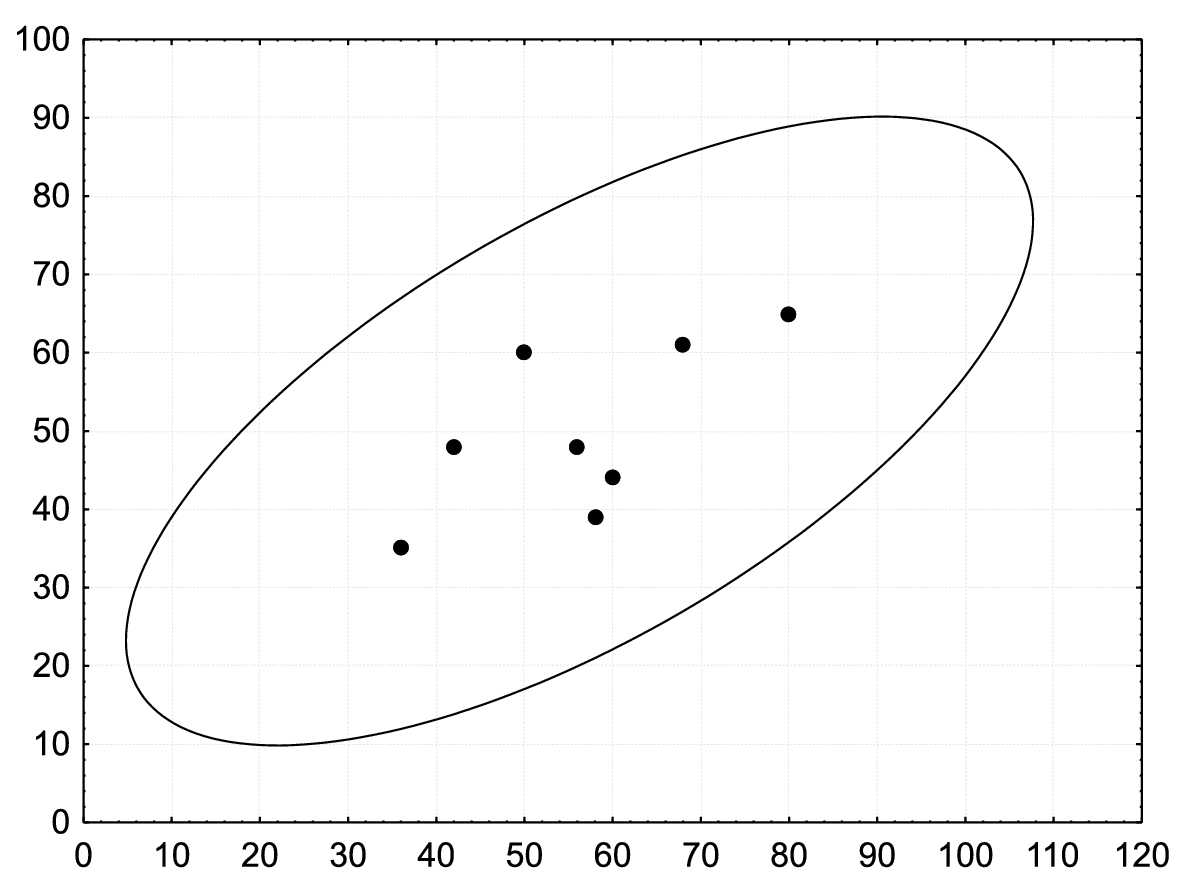
Řešení. Nejprve se musíme přesvědčit, že uvedené výsledky lze považovat za realizace náhodného výběru z dvourozměrného normálního rozložení. Lze tak učinit orientačně pomocí dvourozměrného tečkového diagramu. Tečky by měly vytvořit elipsovitý obrazec.

Obr. 1. Dvourozměrný tečkový diagram

Obrázek svědčí o tom, že předpoklad dvourozměrné normality je oprávněný a že mezi počty bodů z 1. a 2. testu bude existovat určitý stupeň přímé lineární závislosti.

Testujeme proti pravostranné alternativě

Výpočtem zjistíme: V tabulkách najdeme Kritický obor: Protože hypotézu o neexistenci kladné korelace výsledků z 1. a 2. testu zamítáme na hladině významnosti 0,05.