Logistická regrese

Protože nejčastěji se používá logit linkovací funkce

budeme se proto věnovat logistické regresi podrobněji.

Předpokládejme, že závisle proměnná je binární proměnná, která nabývá hodnoty jedna, pokud sledovaný jev nastal, v opačném případě je rovna nule.

Protože jde o regresní model, bude nás zajímat vztah pravděpodobností úspěchu či neúspěchu k hodnotám regresorů (kovariát) budeme tedy zkoumat pravděpodobnost

a

Předpokládejme, že lineární prediktor je roven

a ukážeme, že má smysl uvádět absolutní člen samostatně.

Všimněme se nejprve, že podíl

má bezprostřední interpretaci. Porovnává pravděpodobnost jedničky (tj. výskyt sledovaného jevu při daných hodnotách kovariát) a nuly (nevýskyt sledovaného jevu při daných hodnotách kovariát). Anglickému označení odds odpovídá české označení šance. Hodnota šance není shora ohraničená, zdola však nulou. Pokud zlogaritmujeme šanci, dostaneme logit, který nabývá hodnot od mínus do plus nekonečna.

Nyní budeme předpokládat, že máme jedinou kovariátu která je také binární, takže nabývá dvou různých hodnot, které můžeme bez újmy na obecnosti označit jako 0 a 1. V tom případě jde o kategoriální proměnnou, nebo–li je umělá proměnná k dvouhodnotovému faktoru.

Za těchto podminek je šance pro rovna

takže parametr je roven logitu pravděpodobnosti výskytu sledovaného jevu v bodě 

Pro  dostaneme

Poměr šancí (nebo také křížový poměr, anglicky odds ratio) pro binární je pak roven

takže parametr  je roven logaritmu poměru šancí. Odtud tedy dostáváme, že pokud pravděpodobnost sledovaného jevu nezávisí na hodnotě proměnné je poměr šancí roven jedné, takže platí

I v případě, že vysvětlující proměnná je spojitá, má zajímavou interpretaci především parametr  neboť

takže parametr  vypovídá o změně vztažené k jednotkovému přírůstku nezávisle proměnné tentokrát je to změna logaritmu poměru šancí.

Příklad. V souboru „beetle.RData“ jsou uvedeny údaje o úmrtnosti Potemníka skladištního (Tribolium confusum) v reakci na sirouhlík Datový soubor obsahuje tyto proměnné

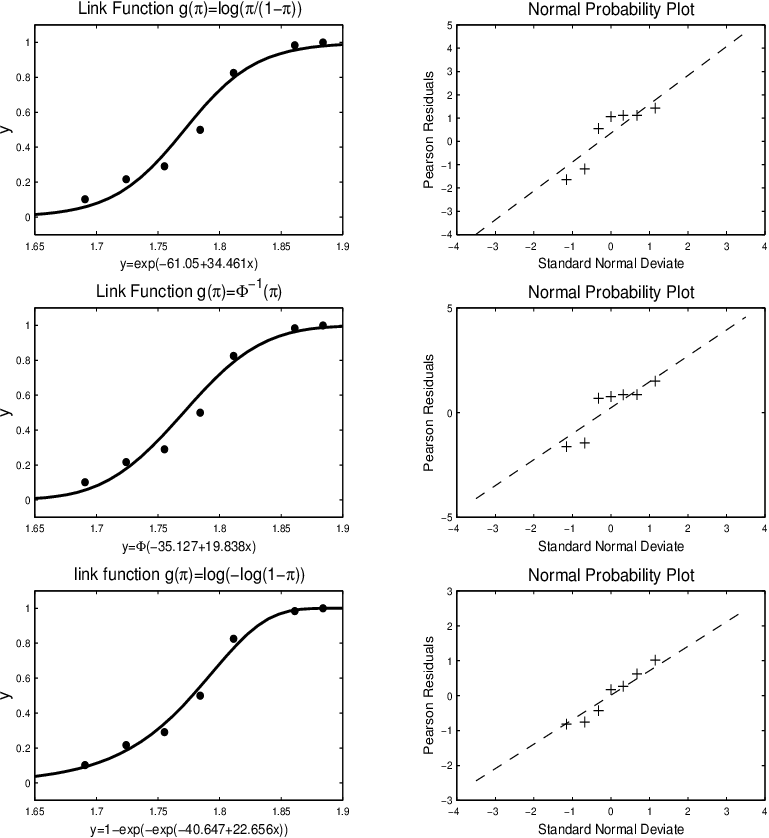
Řešení. Pro modelování závislosti použijeme logistický model, probitový model a model s komplementární log-log linkovací funkcí. Výsledky jsou znázorněny na nasledujícím obrázku.

Obr. 7. Modely pro úmrtnost Potemníka skladištního.