Bodové a intervalové odhady parametrů normálního rozdělení

Nechť    Připomeňme, že platí:

Normální rozdělení s hustotou

má střední hodnotu  a rozptyl . Toto rozdělení má následující vlastnosti:

 rozdělení:

Studentovo t-rozdělení:

Fisherovo-Snedecorovo F-rozdělení:

Věta 5.1. Mějme  a výběrový průměr  a výběrový rozptyl . Pak platí

(1)	Výběrový průměr
(2)	Statistika
(3)	Statistika
(4)	Statistika

Poznámka 5.2. Statistiky , a se nazývají PIVOTOVÉ STATISTIKY, přičemž

	je pivotovou stastistikou pro neznámý parametr		při známém
	-||-
	-||-		při neznámém

Důsledek 5.3. Mějme _, kde  je neznámý parametr a  je známé reálné číslo. Pak

		- je  interval spolehlivo pro střední hodnotu při známém
		- je dolní odhad střední hodnoty  při známém  se spolehlivostí
		- je horní odhad střední hodnoty při známém  se spolehlivostí

Důkaz. Za pivotovou statistiku zvolíme statistiku

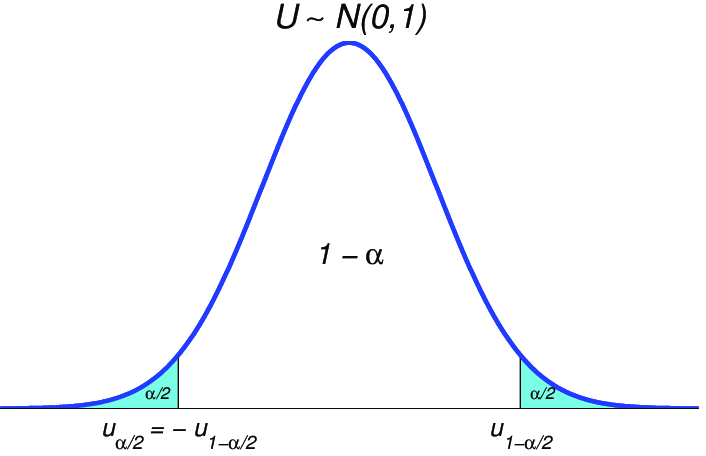	Pro lepší čitelnost místo  budeme psát pouze .   Počítejme

Důsledek 5.4. Mějme , kde a jsou neznámé parametry. Pak

(1)	pro střední hodnotu
		- je  interval spolehlivo pro střední hodnotu  při známém
		- je dolní odhad střední hodnoty při známém  se spolehlivostí
		- je horní odhad střední hodnoty při známém  se spolehlivostí
(2)	pro rozptyl
		- je interval spolehlivosti pro rozptyl
		- je dolní odhad rozptylu se spolehlivostí
		- je horní odhad rozptylu  se spolehlivostí

V dalším si budeme všímat intervalů spolehlivosti pro DVA NEZÁVISLÉ VÝBĚRY.

Veta 5.5. Nechť  je náhodný výběr rozsahu  z normálního rozdělení ,  je jeho výběrový průměr a  jeho výběrový rozptyl.

Dále nechť je náhodný výběr rozsahu z normálního rozdělení   je jeho výběrový průměr a jeho výběrový rozptyl.

Předpokládejme, že oba výběry jsou stochasticky nezávislé, tj. . Pak

(1)	Statistika
(2)	Pokud  pak statistika
(3)	Statistika

Důsledek 5.6. Nechť  je náhodný výběr rozsahu  z normálního rozdělení ,  je jeho výběrový průměr a  jeho výběrový rozptyl.

Dále nechť  je náhodný výběr rozsahu  z normálního rozdělení   je jeho výběrový průměr a  jeho výběrový rozptyl.

Předpokládejme, že oba výběry jsou stochasticky nezávislé, tj. . Pak

(1)	jsou-li   pak interval spolehlivosti pro rozdíl středních hodnot  je tvaru
(2)	Jestliže  a platí , pak  interval spolehlivosti pro rozdíl středních hodnot  je tvaru kde
(3)	Při    je   interval spolehlivosti pro podíl rozptylů  roven

Poznámka 5.7. Ve statistických tabulkách bývají uváděny kvantily F-rozdělení pouze pro hodnoty . Ukážeme, proč není třeba uvádět hodnoty kvantilů pro . Uvažujme místo pivotové statistiky statistiku

Opět označme  a  a počítejme interval spolehlivosti pro takto navrženou pivotovou statistiku

Takže 

a interval spolehlivosti pro  lze vyjádřit i takto

V dalším se zaměříme na interval spolehlivosti pro rozdíl středních hodnot u tzv. PÁROVÝCH VÝBĚRŮ.

Věta 5.8. Nechť  je náhodný výběr z dvourozměrného normálního rozdělení  s parametry 

 

kde

Pro  označme

Pak

je intervalový odhad parametrické funkce  o spolehlivosti .