Problematika příliš velkého nebo příliš malého rozptylu

V praktickém modelování často narážíme na problémy s příliš velkou variabilitou dat (overdispersion) nebo příliš malou variabilitou dat (underdispersion). Existuje řada možných vysvětlení, proč k tomu dochází. Tak například v biologických studiích může být overdispersion důsledkem agregovaného výskytu organismů. Nebo je tento jev důsledkem závislosti v datech, které standardní model nepředpokládá. Příliš malý či velký rozptyl může vzniknout také nezařazením některé důležité vysvětlující proměnné.

Popišme podrobněji tento jev. Předpokládáme, že náhodný výběr  z rozdělení exponenciálního typu se řídí GLM modelem, tj. má sdruženou pravděpodobnostní funkci nebo sdruženou hustotu tvaru

Předpokládejme, že pro hustotu exponenciálního typu platí

kde jsou známé apriorní váhy a je neznámý tzv. faktor měřítka (scale factor) nebo bývá též nazýván rušivý parametr.

Při testování vhodnosti modelu hraje důležitou roli tzv. (škálová) deviace, kterou můžeme vyjádřit

a nazveme neškálovou deviací (unscaled deviance). Protože platí

neboť střední hodnota rozdělení je rovna počtu stupňů volnosti, pak

Další často používanou mírou vhodnosti modelu je tzv. zobecněná Pearsonova statistika

a proto dalším momentovým odhadem založeným na této statistice je

Přehled rušivých parametrů pro některá rozdělení exponenciálního typu je dán v následující tabulce:

Problém s příliš velkou či malou variabilitou se týká těch rozdělení, u kterých má být scale parametr roven jedné, tj. binomického a Poissonova rozdělení. Pokud pro reálná data dojde k tomu, že například pro binomické či Poissonovo rozdělení je rozptyl větší než střední hodnota, pak jde o overdispersion. Pokud je například u dat, pro která jsme předpokládali Poissonovo rozdělení, rozptyl naopak menší než střední hodnota, pak jde o underdispersion. V těchto případech není hodnota disperzního (scale) parametru (jakožto poměru ) rovna 1. Ve výpisu výsledků modelu nás na tuto situaci upozorní výrazně větší (menší) hodnota reziduální (tedy nevysvětlené) deviace ve srovnání s reziduálním počtem stupňů volnosti, což je střední hodnota rozdělení.

V prostředí R je k řešení tohoto problému k dispozici modifikovaná volba pro třídu exponenciálního rozdělení. V případě binomického rozdělení máme možnost volby

a pro Poissonovo rozdělení

Nejde o nový typ exponenciálního rozdělení, ale o změnu ve výpočtu druhého momentu, pro jehož odhad se použije jednoduchý momentový odhad disperzního parametru  Výsledná korekce rozptylu je pak důležitá při testování hypotéz, neboť zohledňuje vyšší/nižší variabilitu v datech a zabraňuje tak nadbytku/nedostatku falešně pozitivních výsledků testů hypotéz o parametrech modelu.

Příklad. V souboru „bees.RData“ jsou uvedeny údaje o aktivitě včel v závislosti na čase. Jednou z důležitých charakteristik při zkoumání včelí aktivity je počet včel, které opustí úl kvůli práci ve vnějším prostředí. Studie se zabývala měřením této veličiny během několika slunečných dní v závislosti na čase během dne. Datový soubor obsahuje tyto proměnné

Modelujte závislost počtu včel, které opustí úl, na čase během dne.

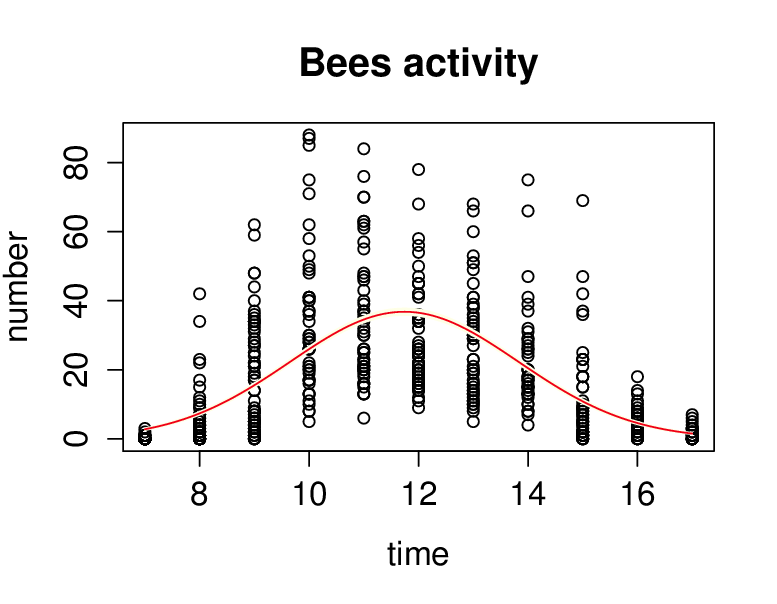
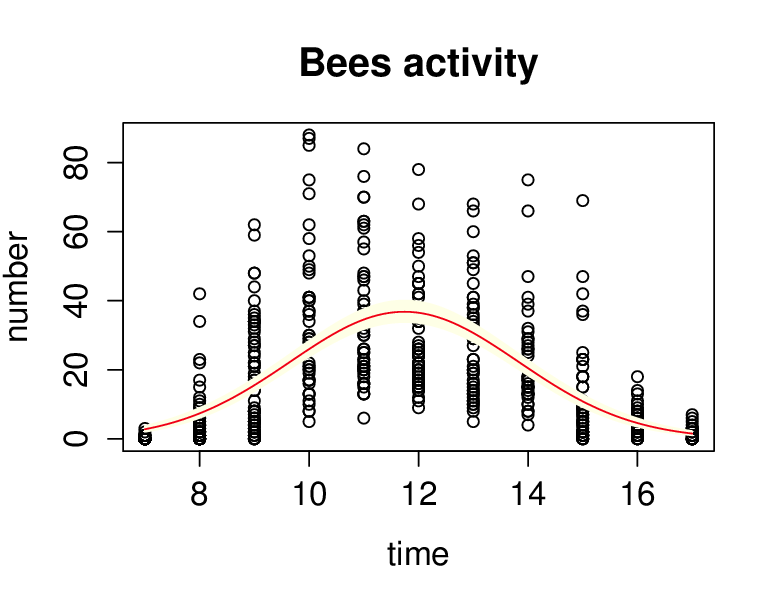
Řešení. Budeme předpokládat, že závisle proměnná number má Poissonovo rozdělení a pro modelování závislosti použijeme poissonovský model. Jako linkovací funkci zvolíme kanonickou, tj. logaritmus. Do modelu vstupuje jediná vysvětlující proměnná time a přidáme také její druhou mocninu. Po výpočtu všech potřebných parametrů je vidět, že  hodnota reziduální deviace (4 879,3) je nepoměrně vyšší než počet stupňů volnosti (501), což je střední hodnota. Je tedy zřejmé, že došlo k „overdispersion“ a v jazyce je třeba volit family=quasipoisson. Použití této volby  neovlivňuje odhady koeficientů, ale mění jejich odhady variability, což se projeví např. v intervalu spolehlivosti. To je vidět i z grafického srovnání obou výsledků, viz obr. Konkrétní GLM modely 9 a obr. Konkrétní GLM modely 10.

Obr. 9. Odhad regresní funkce bez vyrovnání se s problematikou velkého rozptylu.

Obr. 10. Odhad regresní funkce s vyrovnáním se s problematikou velkého rozptylu.