Rozšířený lineární regresní model a vážená metoda nejmenších čtverců

V některých případech je nutné řešit poněkud obecnější regresní úlohu, než jsme dělali až doposud. Budeme se snažit rozšířit
regresní model i na případ, kdy rozptyl není homogenní.

Nechť platí lineární regresní model s obecnější varianční maticí

Také v tomto případě jsou  a  neznámé parametry a matice  je (zpravidla známá) pozitivně definitní matice.

Následující věta ukazuje, jakým způsobem lze provést odhad neznámých parametrů v tomto obecnějším případě.

Věta 6.1. (Aitkenův odhad). Mějme regresní model  plné hodnosti, kde .  Pak odhad pomocí metody nejmenších čtverců je roven

Poznámka 6.2. V případě, že matice  je diagonální, mluvíme o vážené regresi a metodě nejmenším čtverců, pomocí které byly provedeny odhady, se v tomto případě říká vážená metoda nejmenších čtverců.

Příkladem takového modelu je situace, kdy i-tá složka vektoru  je průměrem  nezávislých pozo ování se stejnou střední hodnotou a stejným rozptylem . Potom

a regresní model je tvaru

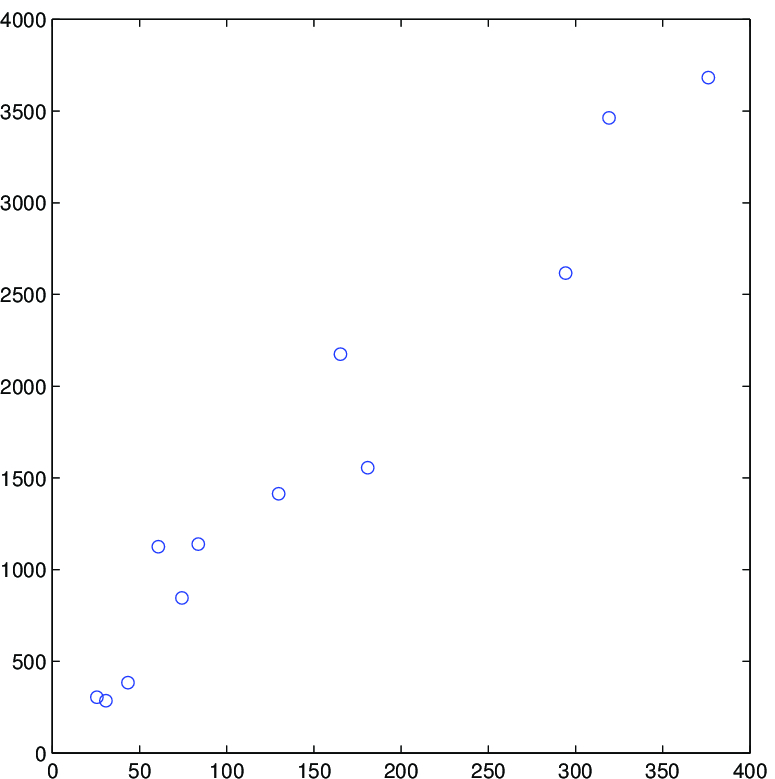
Příklad 6.3. Analyzujte data o počtu pracovních hodin za měsíc spojených s provozováním anesteziologické služby v závislosti na velikosti spádové populace nemocnice (viz následující tabulka). Údaje byly získány ve 12 nemocnicích ve Spojených státech.

ZÁVISLOST POČTU PRACOVNÍCH HODÍN  NA VELIKOSTI POPULACE

 

 

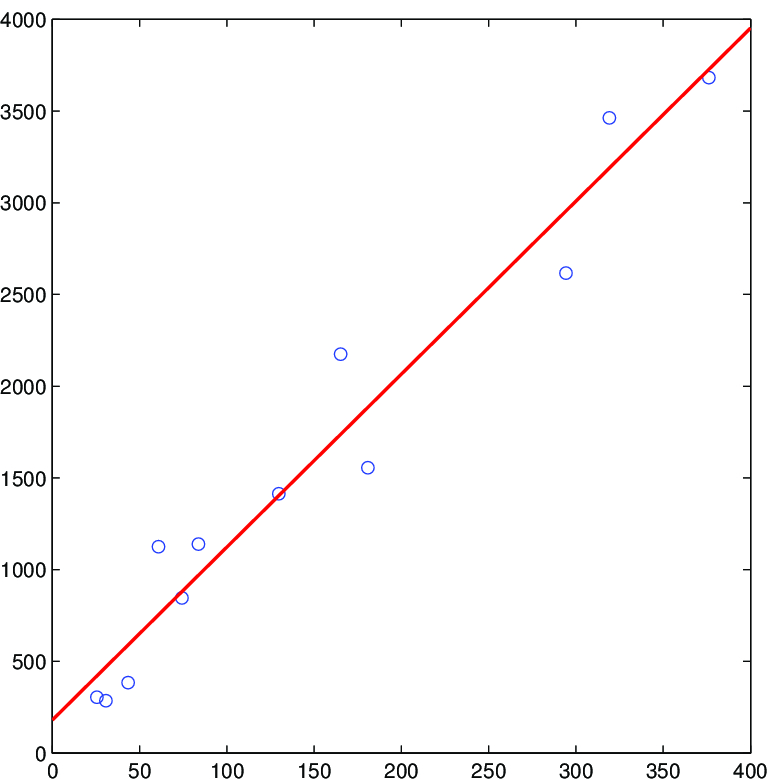
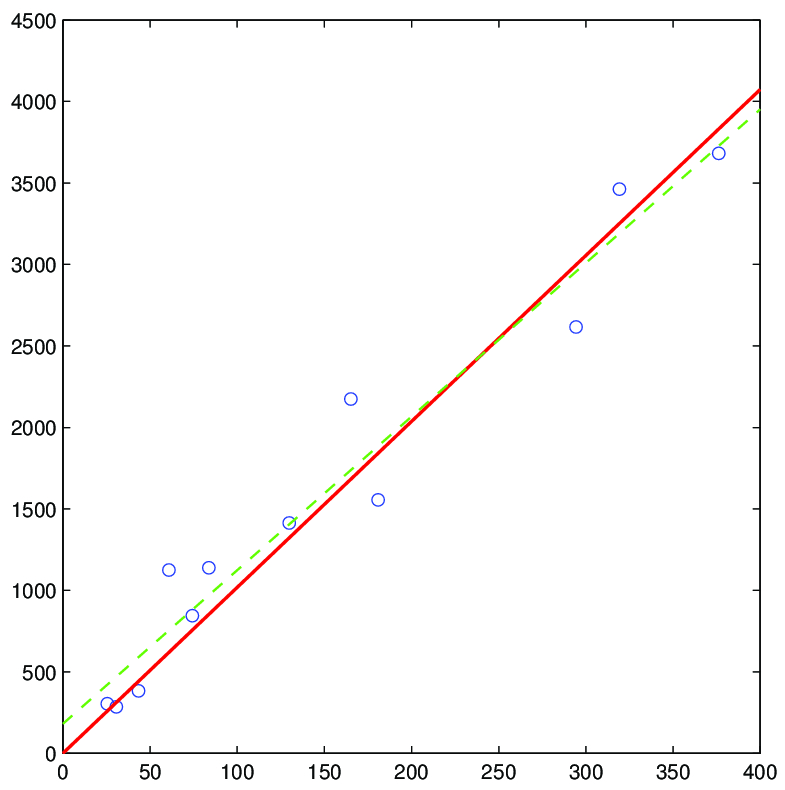
Řešení. Graf naznačuje lineární vztah mezi pracovní dobou a velikostí populace, a tak budeme pokračovat kvantifikací tohoto vztahu pomocí přímky  

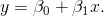
	Používáme-li model regresní analýzy pro statistické zpracování našich dat,je dobré ověřit předpoklady, ze kterých model vychází. Shrňme je v následujících třech bodech.
	(1)	Závisle proměnná  (pracovní doba) má normální rozdělení pro každou hodnotu nezávisle proměnné  (velikost populace).
	(2)	Rozptyl závisle proměnné je stejný pro každou hodnotu nezávisle proměnné .
	(3)	Rozptyl závisle proměnné je stejný pro každou hodnotu nezávisle proměnné .
	Pro tuto chvíli předpokládejme, že pro náš příklad jsou tyto předpoklady splněny.

Odhad absolutního členu  a směrnice  regresní přímky a jejich statistické charakteristiky jsou uvedeny v další tabulce. Směrodatná chyba koeficientu je výběrová směrodatná odchylka odhadovaného parametru, tj.

a

(Ve statistických programech je obvykle označována anglicky jako Standard Error.)

 

STATISTICKÉ CHARAKTERISTIKY LINEÁRNÍ REGRESE

 

Z tabulky  tedy dostáváme:

To je třeba interpretovat jako odhad průměrné hodnoty počtu pracovních hodin pro populaci s danou velikostí. Očekáváme, že na každých dalších 1 000 lidí stoupne za měsíc počet pracovních hodin o 9,429, což je směrnice regresní přímky. Uvědomte si, že absolutní člen (180,658) značí průměrný počet pracovních hodin, když je populace rovna nule. To zřejmě nedává smysl a mělo by nám to připomenout, že model by se měl používat pouze v tom rozmezí obou veličin, v němž se pohybovaly pozorované hodnoty. V tomto případě to znamená od 26 do 370. Je ovšem pravda, že dosažená hladina významnosti pro absolutní člen je přibližně 0,19, a nelze tedy říci, že by se absolutní člen  významně lišil od nuly.

Připomeňme, že tyto výsledky jsme spočítali pro náhodný výběr 12 nemocnic. Kdybychom teď zvolili jiný náhodný výběr 12 nemocnic, dostali bychom odlišný odhad směrnice a absolutního členu. Určeme proto intervaly spolehlivosti neznámých parametrů  a .

Oboustranný interval spolehlivosti pro	Oboustranný interval spolehlivosti pro

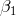
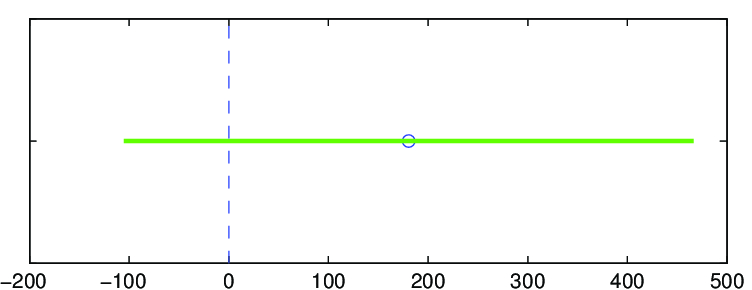
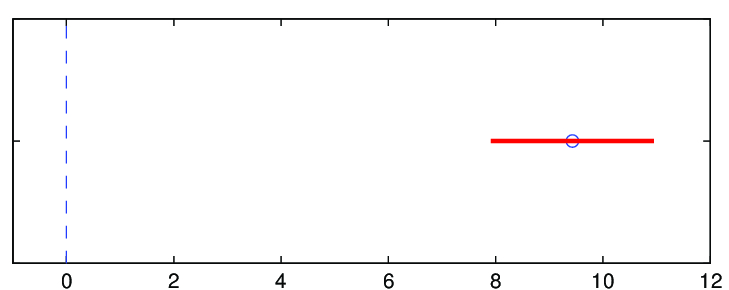
Na základě výběru 12 nemocnic můžeme říci, že neznámý parametr  leží mezi -105,394 a 466,709 a neznámý parametr , tj. parametr změny průměrného počtu pracovních hodin v závislosti na změně velikosti populace (v tisících), leží mezi 7,912 a 10,946 pracovními hodinami za měsíc.

Protože interval spolehlivosti pro  pokrývá nulu, nelze potvrdit, že se významně liší od nuly. Naproti tomu interval spolehlivosti pro  nulu nepokrývá, tedy se významně liší od nuly, jinak řečeno počet pracovních hodin skutečně lineárně závisí na rozsahu spádové populace.

Pokud bychom uvažovali regresi procházející počátkem (plná čára) a výsledek srovnali s obecnou regresní přímkou (čárkovaná čára), dostaneme následující odhady

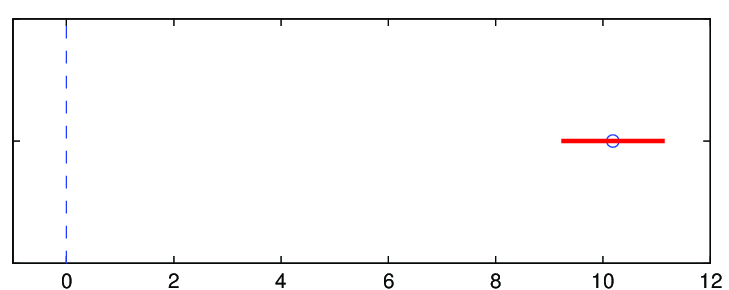
Oboustranný interval spolehlivosti pro
Protože interval spolehlivosti pro  nulu nepokrývá, opět jsme prokázali, že se významně liší od nuly, tj. počet pracovních hodin skutečně lineárně závisí na rozsahu spádové populace.