
Úvod
Nejprve se pokusíme sestavit matematický model jednoduchého procesu, děje, který lze nějak kvantifikovat a který se odehrává v průběhu času. Konkrétně půjde o model růstu nějaké populace. Přitom si budeme představovat, že proces pozorujeme nebo popisujeme v oddělených časových okamžicích. Běh času si tedy budeme představovat jako diskrétní, jako plynoucí v nějakých krocích nebo taktech, jejichž trvání budeme považovat za jednotkové. Tato představa bude podstatná.
Základním objektem vystupujícím v modelu bude posloupnost. Právě členy posloupnosti budou vyjadřovat stav procesu v jednotlivých okamžicích. U posloupností si budeme všímat její monotonnosti, ohraničenosti, existence nebo neexistence limity, případně jiné charakteristiky chování posloupnosti. To ukazuje, že je užitečné připomenout některé základní poznatky o posloupnostech případně je uvést v nových souvislostech. Zejména si ukážeme, že pro posloupnosti můžeme vytvořit kalkulus, který je analogií diferenciálního a integrálního počtu pro funkce.
Jednoduchý model růstu populace
Představme si populaci složenou z nějakých organismů; mohou to být obratlovci, rostliny, mikrobi - na zvolené úrovni abstrakce na jejich povaze nezáleží. Všechny jedince budeme považovat za stejné, jeden od druhého se nijak neliší, v průběhu svého života se nijak nemění. Do naší úvahy zahrneme jediné dva děje, konkrétně že jedinci vznikají (rodí se, líhnou, klíčí, pučí, ...) a zanikají (umírají, hynou, dělí se, ...). Jako jedinou kvantitativní charakteristiku populace budeme uvažovat její velikost;ta může být vyjádřena počtem jedinců, populační hustotou, celkovou biomasou a podobně. Dále si budeme představovat, že velikost populace zjišťujeme v pravidelných časových intervalech, jinak řečeno, že máme nějakou „přirozenou“ jednotku času, takže můžeme časové okamžiky
očíslovat přirozenými čísly 0,1,2,... . Je celkem jasné, že
| (velikost populace v čase |
|
+ (množství jedinců vzniklých v časovém intervalu od
|
|
- (množství jedinců uhynulých v časovém intervalu od
|
Z tohoto pojmového modelu vytvoříme model matematický tak, že zavedeme veličinu závislou na čase, tedy
kterou budeme interpretovat jako (pozorovanou) velikost populace v časovém okamžiku
Dále označíme
množství jedinců vzniklých v časovém intervalu od
do
a
množství jedinců uhynulých v tomto období. Symboly jsou voleny tak, že
označuje veličinu, kterou chceme znát,
je zkratkou slova „birth“ a
slova „death“.
Uvedené slovně vyjádřené rovnici nyní můžeme dát tvar
|
|
(1) |
Abychom z této rovnice mohli spočítat velikost populace v jednotlivých časových okamžicích, potřebujeme ještě specifikovat veličiny a
Vzhledem k předpokladu, že všichni jedinci jsou stejní, můžeme očekávat, že každý z nich „vyprodukuje“ během časového intervalu jednotkové délky určité stejné množství živých potomků; označme toto množství
Alternativně bychom mohli říci, že
je střední hodnota počtu potomků jedince za jednotkový časový interval. Hodnota
tedy nemusí být celé číslo. Celkové množství jedinců vzniklých v časovém intervalu od
do
tedy bude
|
|
(2) |
Z téhož předpokladu také můžeme odvodit, že každý jedinec má v libovolném intervalu jednotkové délky stejnou pravděpodobnost, že uhyne; označme tuto pravděpodobnost Klasicky spočítáme pravděpodobnost, že jedinec během jednotkového intervalu uhyne jako podíl množství uhynulých jedinců a množství všech jedinců, tj.
neboli
|
|
(3) |
Možnost, že nějaký jedinec vznikne i zanikne v témže jednotkovém časovém intervalu, nemá na vztahy Přípravné úvahy (2), Přípravné úvahy (3) vliv. Takoví jedinci by totiž nemohli být zahrnuti mezi živé potomky, kterých je a tím pádem by v odvozených rovnostech vůbec nefigurovali.
Při odvození vztahu Přípravné úvahy (2) jsme však uvažovali, jako by se množství jedinců, kteří žili v časovém okamžiku v průběhu intervalu do
neměnilo. Mlčky jsme tedy přijali další zjednodušující předpoklad: k rození dochází „krátce po začátku“ uvažovaného časového intervalu, k úhynům „krátce před jeho koncem“.
Vyjádření Přípravné úvahy (2) a Přípravné úvahy (3) dosadíme do rovnice Přípravné úvahy (1). Dostaneme
nebo po triviální úpravě
|
|
(4) |
Parametr v této rovnici nazýváme porodnost (birth rate); tento parametr je kladný, neboť v nevyhynulé populaci musí noví jedinci vznikat. Parametr
nazýváme úmrtnost (death rate); poněvadž vyjadřuje pravděpodobnost, nabývá hodnot mezi 0 a 1 - úmrtí je možné, ale není nutné. Tedy
|
|
(5) |
Označíme-li
|
|
(6) |
můžeme rovnici Přípravné úvahy (4) zapsat v kratším tvaru
|
|
(7) |
parametr nazveme koeficient růstu (růstový koeficient, growth rate). Vyjadřuje relativní přírůstek populace za jednotku času. Podle podmínek Přípravné úvahy (5) platí
|
|
(8) |
Rovnost Přípravné úvahy (7) můžeme chápat jako rekurentní formuli pro geometrickou posloupnost
s kvocientem dobře známou ze střední školy. Pokud tedy na počátku, tj. v čase
je velikost populace rovna
|
|
(9) |
kde je nějaké kladné číslo, pak velikost populace v libovolném časovém okamžiku
je rovna
|
|
(10) |
Dostáváme tak první závěr: velikost populace roste jako geometrická posloupnost („populace roste geometrickou řadou“). Tento závěr - ovšem odpozorovaný na růstu obyvatelstva severoamerických osad, nikoliv odvozený uvedeným postupem - zpopularizoval Thomas Malthus ve svém slavném Pojednání o principech populace z roku 1798. Proto rovnici Přípravné úvahy (7) s počáteční podmínkou Přípravné úvahy (9) budeme nazývat malthusovský model růstu populace.
Závěr bychom ale měli formulovat opatrněji: pokud se populace vyvíjí podle modelu (nebo snad podle přírodního zákona?) vyjádřeného rovností Proto rovnici Přípravné úvahy (7) a na počátku má velikost rovnu , pak její velikost v časovém okamžiku
je dána výrazem na pravé straně rovnosti Proto rovnici Přípravné úvahy (10). Je-li přitom
tj. porodnost je větší než úmrtnost, pak velikost populace roste nade všechny meze,
je-li
tj. úmrtnost je větší než porodnost, pak populace vymírá,
Pokud by
tj. porodnost by se vyrovnala s úmrtností, velikost populace by se neměnila,
v každém časovém okamžiku
Geometrický růst populace skutečně může být pozorován v případech, kdy populace je malá a prostředí, ve kterém se vyvíjí, je prakticky neomezené; jako např v době počátečního osídlení Ameriky imigranty z Evropy a západní Afriky, nebo růst kolonie bakterií na živném substrátu. Malthusovský model Přípravné úvahy (7) tedy za jistých podmínek popisuje růst reálné populace. Ovšem žádná populace nemůže růst nade všechny meze, přinejmenším proto, že povrch Země je konečný.
Nyní jsme tedy v situaci, že pro popis růstu (nebo přesněji pro popis vývoje velikosti) populace máme matematický model Přípravné úvahy (4), který adekvátně popisuje skutečnost za jistých, dosti omezujících předpokladů. Chtěli bychom však mít model, který zachovává „dobré vlastnosti“ modelu Přípravné úvahy (4), tj. správně popisuje počáteční fáze růstu malé populace, ale nemá jeho „vlastnost špatnou“, tj. nepředpovídá nerealistický růst nade všechny meze.
V omezeném prostředí velká populace spotřebovává velké množství omezených zdrojů, na jedince připadne jejich menší podíl a proto se mu nebude dostávat energie k reprodukci. Je-li tedy v prostředí s omezenými zdroji velká populace, je její porodnost (počet potomků na jedince) menší, než by byla v případě, že by populace byla malá.
Velká populace znečišťuje prostředí produkty svého metabolismu; žádný organismus ale nemůže žít v prostředí tvořeném odpady jeho činnosti nebo života. Je-li tedy populace v omezeném prostředí velká, na jedince připadne větší množství produkovaných odpadních látek, které bývají toxické a proto se úmrtnost v populaci zvětší.
Těmito úvahami můžeme dojít k závěru, že u velké populace je malá porodnost nebo velká úmrtnost. Tyto jevy se vzájemně zesilují podle Přípravné úvahy (6), růst populace působí pokles růstového koeficientu. Při „vylepšování“ modelu Přípravné úvahy (4) tedy konstantní koeficient růstu nahradíme nějakým výrazem závislým na velikosti populace, nějakou funkcí proměnné
Model růstu populace tedy může mít obecný tvar
|
|
(11) |
Přitom funkce je definována pro nezáporné hodnoty argumentu
a je klesající. Chceme, aby model Přípravné úvahy (7) byl speciálním případem
modelu Přípravné úvahy (11) pro „malé“ velikosti populace. Přesněji tento požadavek vyjádříme ve tvaru
|
|
(12) |
V tomto případě se nazývá vnitřní koeficient růstu (intrinsic growth rate). Vyjadřuje maximální možný relativní přírůstek velikosti populace za jednotku času, tj. takový přírůstek, který by populace měla v prostředí s neomezenými zdroji.
Existující populace žijí v dynamické rovnováze se svým prostředím, jejich velikost se dlouhodobě nemění, přestože jedinci se rodí a umírají. Toto pozorování vede k předpokladu, že pro každou populaci existuje nějaká „rovnovážná velikost“. Pokud by populace byla větší, spotřebovávala by více zdrojů nebo produkovala více odpadů a její růstový koeficient by byl menší než 1. Naopak, kdyby populace byla menší než „rovnovážná“, měla by nadbytek zdrojů na jedince a „přebytečná“ energie by se mohla využít pro reprodukci. Růstový koeficient takové populace by byl větší než 1. Tyto úvahy nyní vyjádříme tak, že pro klesající funkci existuje konstanta
taková, že
|
|
(13) |
Hodnota vyjadřuje kapacitu (úživnost) prostředí.
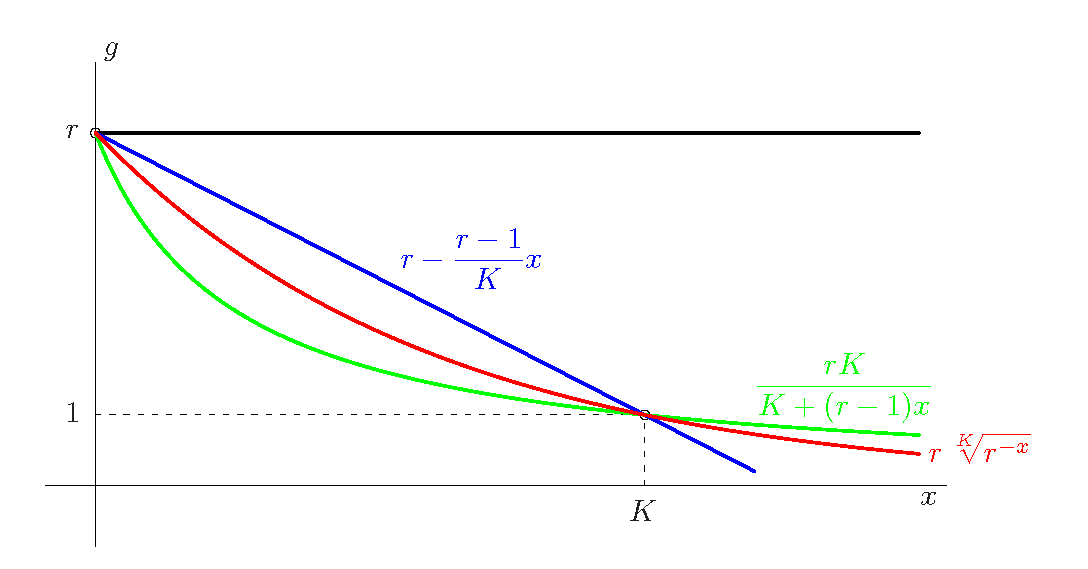
Funkce vystupující v modelu Přípravné úvahy (11) je tedy klesající a splňuje podmínky Přípravné úvahy (12), Přípravné úvahy (13). Tuto funkci potřebujeme dále nějak specifikovat.
 |
|
Obr. 1. Různé možnosti volby funkce g na pravé straně obecného modelu Přípravné úvahy (11) růstu populace v prostředí s omezenými zdroji.
|
Nejjednodušší volbou je lineární funkce,
tato funkce je na obr. Přípravné úvahy 1 znázorněna modrou přímkou. Model Přípravné úvahy (11) tedy získá tvar
|
|
(14) |
Tato rovnice se nazývá logistická. Jako model růstu populace ji patrně poprvé použil John Maynard Smith ve slavné knize Mathematical Ideas in Biology, Cambridge Univ. Press, 1968.
Rovnici Přípravné úvahy (14) lze opět chápat jako rekurentní formuli pro nějakou posloupnost. Pro obecný člen takové posloupnosti však neznáme vzoreček. Aspoň ale můžeme vypočítat prvních několik členů této posloupnosti pro různé hodnoty parametrů. Tyto simulace provedeme pro hodnoty a
to lze interpretovat jako růst populace v neobsazeném prostředí, do něhož invadovalo několik jedinců, rovnovážnou velikost populace přitom považujeme za jednotkovou.
| Animace 1- logisticka regrese.pdf |
| Obr. 2. Řešení logistické rovnice x(t+1)=x(t)(r-(r-1)x(t)) s počáteční hodnotou x(0)=0,01 pro různé hodnoty parametru r. |
Vidíme, že pro malé hodnoty koeficientu přesněji pro
populace roste. Pro malé hodnoty
růst připomíná geometrickou posloupnost, poté se stane skoro lineárním (připomíná aritmetickou posloupnost s kladnou diferencí), pak se zpomalí až dosáhne hodnoty kapacity prostředí a růst ustane. Jinak řečeno, posloupnost zadaná rekurentně rovností Přípravné úvahy (14) je rostoucí omezenou posloupností, pro niž platí
|
|
(15) |
Pokud je hodnota růstového koeficientu větší, přesněji pokud je
posloupnost překročí hodnotu kapacity prostředí, ale s tlumenými oscilacemi se na této hodnotě postupně ustálí. Stále tedy platí Přípravné úvahy (15), ale posloupnost již není monotonní.
Při ještě větší hodnotě se hodnoty posloupnosti neustálí na kapacitě prostředí, ale kolísají kolem ní. Pro menší
pravidelně, pro velká
již z obrázků žádnou pravidelnost vypozorovat nemůžeme.
Z těchto pozorování můžeme uzavřít, že model Přípravné úvahy (14) může popisovat jak populaci, jejíž velikost je v dynamické rovnováze se svým prostředím (takové jsou např. populace velkých savců, nazýváme je -stratégové - ustálí se na hodnotě
), tak populaci, jejíž velikost kolísá (to je typické např. pro drobné hlodavce, nazýváme je
-stratégové - mají velkou hodnotu
). Jeden model popisuje různé ekologické jevy. To je jeho velká přednost a proto je model Přípravné úvahy (15) dobrým adeptem na „objevený přírodní zákon“.
| Animace 2 - Bevertonova-Holtova rovnice.pdf |
|
Obr. 3. Řešení Bevertonovy-Holtovy rovnice
|
Velká nevýhoda modelu Přípravné úvahy (14) však spočívá v tom, že pro velkou počáteční hodnotu jsou její další hodnoty záporné, konkrétně pro
je
Reálná populace nemůže mít zápornou velikost. Přitom velká počáteční hodnota může vyjadřovat např. to, že se v důsledku nějaké ekologické disturbance skokem zmenšila úživnost prostředí. Model Přípravné úvahy (14) tedy není dostatečně obecný.
Naznačený problém modelu Přípravné úvahy (14) spočívá v tom, že funkční hodnoty funkce jsou pro velké hodnoty argumentu záporné. Potřebujeme tedy klesající funkci, která má vlastnosti Přípravné úvahy (12), Přípravné úvahy (13) a navíc je pro všechny hodnoty argumentu kladná. Takovou funkcí může být funkce lomená,
která je na obr. Přípravné úvahy 1 znázorněna zelenou křivkou. Příslušný model má tvar
|
|
(16) |
Tento model zavedli Raymond Beverton a Sidney Holt1, nezávisle na nich a jiným způsobem ho odvodila Evelyn Pielou2. Často bývá nazýván Bevertonova-Holtova logistická rovnice nebo logistická rovnice Pielou.
Opět můžeme vypočítat několik prvních členů posloupnosti pro kapacitu prostředí , s počáteční hodnotou
a s různými hodnotami koeficientu
viz obr. Přípravné úvahy 3 . V tomto případě vidíme, že výsledná posloupnost vždycky roste a dosáhne kapacity prostředí, tedy pro libovolnou hodnotu
platí vztah Přípravné úvahy (15). Model Přípravné úvahy (16) je tedy vhodný pouze pro popis populace
-stratégů.
Cenou za odstranění nedostatku v modelu Přípravné úvahy (14) jeho nahrazením modelem Přípravné úvahy (16) je ztráta universality. Oba modely Přípravné úvahy (14) i Přípravné úvahy (16) mají nějaké „dobré vlastnosti“, ale také „nedostatky“. Zkusíme v modelu Přípravné úvahy (11) použít funkci která je „něco mezi“ funkcí lineární a lomenou.
Elementární klesající kladná funkce, která má vlastnosti Přípravné úvahy (12) a Přípravné úvahy (13) a jejíž hodnoty jsou mezi hodnotami funkce lineární a lomené, je funkce exponenciální
viz na obr. Přípravné úvahy 1 červenou křivku mezi modrou přímkou a zelenou křivkou. Příslušný model je tvaru
|
|
(17) |
a zavedl ho William Ricker3. Bývá nazýván Rickerova (logistická) rovnice. Vypočítáme-li z něho několik prvních členů posloupnosti pro kapacitu a s počáteční hodnotou
pro různé hodnoty růstového koeficientu
vidíme na obr. Přípravné úvahy 4 , že model Přípravné úvahy (17) je universální jako model Přípravné úvahy (14) a nemá jeho vadu.
Ještě si můžeme povšimnout skutečnosti, že malthusovský model Přípravné úvahy (7) je mezním případem všech logistických modelů Přípravné úvahy (14), Přípravné úvahy (16) a Přípravné úvahy (17) také pro Malthusovský model proto můžeme považovat za popis růstu populace v prostředí s neomezenými zdroji, tj. s nekonečnou úživností.
| Animace 3 - Rickerova rovnice.pdf |
|
Obr. 4. Řešení Rickerovy rovnice x(t+1)=x(t)r1-x(t) s počáteční hodnotou x(0)=0,01 pro různé hodnoty parametru r.
|
1R. J. H. Beverton and S. J. Holt, On the dynamic of exploited fish populations. Fisheries Investigations Series 2(19). Ministry of Agriculture, Fisheries, and Food, London, UK, 1957
2E. C. Pielou, Mathematical Ecology. Wiley Interscience, 1977
3W. E. Ricker, Stock and recruitment. J.Fish.Res.Board Can., 11:559-623, 1954
| Název | Zadal | |
|---|---|---|
| doc. RNDr. Zdeněk Pospíšil, Dr | 1,19 MB | |
| doc. RNDr. Zdeněk Pospíšil, Dr | 1,16 MB | |
| doc. RNDr. Zdeněk Pospíšil, Dr | 1,59 MB |




