Zavedeme náhodnou funkci tak, že diskrétní náhodná veličina vyjadřuje velikost rodové linie v -té generaci. Bude nás zajímat očekávaný počet příslušníků rodové linie v -té generaci,

(97)

Označme pravděpodobnost, že rodová linie má v -té generaci právě příslušníků,

(98)

Zejména tedy vyjadřuje pravděpodobnost, že jedinec má právě bezprostředních potomků,

(99)

Hodnoty jakožto pravděpodobnosti splňují pro libovolné vztahy

(100)

Pro , definujeme funkci jako součet nekonečné řady

(101)

Poloměr konvergence této řady je podle Aplikace (100) roven alespoň 1. Pro funkce podle Aplikace (99) a Aplikace (90) platí

(102)

Dále derivováním definiční rovnosti Aplikace (101) podle dostaneme

takže podle Aplikace (98) a Aplikace (97) je

(103)

O počtech bezprostředních potomků různých jedinců předpokládáme, že jsou stochasticky nezávislé. Pravděpodobnost, že dva jedinci budou mít celkem bezprostředních potomků, je tedy dána součtem součinů

a obecně pravděpodobnost, že jedinců bude mít dohromady bezprostředních potomků, je dána součtem

Předpoklad o nezávislosti počtu bezprostředních potomků nějakého jedince a počtu jeho sourozenců vyjádříme nyní tak, že pravděpodobnost jevu, že rodová linie v -ní generaci má velikost právě jedinců a ti mají dohromady bezprostředních potomků, je dána součinem

Pravděpodobnost že jedinec má v -té generaci právě potomků, je pravděpodobností jevu, že jedinec má v -ní generaci právě jednoho potomka a ten má právě bezprostředních potomků, nebo jedinec má v -ní generaci právě dva potomky, kteří mají celkem bezprostředních potomků, atd. Popsané jevy jsou zřejmě neslučitelné, takže

(104)

Jev, že jedinec nemá v -té generaci potomky, je totožný s jevem, že jedinec nemá v -ní generaci potomka, nebo má v -ní generaci jednoho potomka, který nemá žádného bezprostředního potomka, nebo jedinec má v -ní generaci právě dva potomky, z nichž žádný nemá bezprostředního potomka, nebo ... . Z této úvahy dostáváme

(105)

S využitím vztahů Aplikace (104), Aplikace (105) a definice (Cauchyova) součinu mocninných řad dostaneme

Odtud a z Aplikace (102) dostáváme, že hodnoty funkcí můžeme počítat rekurentně ze vztahů

Derivováním uvedené rekurentní formule podle obdržíme

(106)

Dosazením a porovnáním tohoto vztahu s Aplikace (103), Aplikace (91) a Aplikace (94) vidíme, že

Očekávaný počet příslušníků rodové linie v -té generaci je tedy řešením počáteční úlohy

neboť zakladatel rodové linie je jistě jeden. Řešením této jednoduché úlohy je geometrická posloupnost

(107)

Dostáváme tak výsledek: Pokud je střední počet potomků jedince větší než 1, pak lze očekávat, že velikost rodové linie bude růst geometricky; přitom ale podle výsledku v Mizení rodové linie nelze vyloučit, že rodová linie vymře.

Vedle očekávané velikosti rodové linie v -té generaci, tj. střední hodnoty veličiny je důležitou charakteristikou také rozptyl velikosti rodové linie, tedy veličina

Pro její vyšetřování využijeme vlastností vytvořující funkce náhodné veličiny která je dána rovností Aplikace (101). Platí¹

takže

(108)

Derivováním formule Aplikace (106) podle dostaneme

(109)

Poněvadž funkce je vytvořující funkcí náhodné veličiny platí pro ni analogie rovnosti Aplikace (108), tj.

podle Aplikace (94). Po dosazení do Aplikace (109) dostaneme s využitím Aplikace (91), Aplikace (103) rovnost

a po úpravě

Na počátku je celá rodová linie tvořena pouze „zakladatelem rodu“, tj. náhodná veličina nabývá jediné hodnoty a proto je její rozptyl nulový,

Odtud a z předchozí rovnosti dostáváme, že rozptyl velikosti rodové linie v čase je řešením počáteční úlohy pro lineární nehomogenní rovnici prvního řádu

Podle věty Lineární rovnice 2.5 a jejího důsledku Lineární rovnice 2.7 je řešení této úlohy dáno rovností

(110)

pro a

(111)

pro

Z tohoto vyjádření plyne, že pro relativní variabilitu velikosti rodové linie, tj. pro podíl její směrodatné odchylky a střední hodnoty, platí

takže

Tento výsledek je jen jinou formulací výsledku již známého. Pokud střední počet potomků jedince nepřesahuje 1, pak rodová linie v konečném čase jistě vymře. Je-li tj. pokud očekávaná velikost rodové linie roste jako geometrická posloupnost, je i v dostatečně vzdálené generaci jistá nenulová pravděpodobnost jejího vymření. Tato pravděpodobnost roste s rostoucí variabilitou počtu bezprostředních potomků a klesá s rostoucí rychlostí růstu rodové linie.

Z vyjádření Aplikace (110), Aplikace (111) rozptylu velikosti rodové linie v -té generaci můžeme ještě snadno vypočítat, že

Pokud tedy rodová linie může dlouhodobě přežívat, pak rozptyl její velikosti asymptoticky roste jako geometrická posloupnost s kvocientem Jinak řečeno, směrodatná odchylka velikosti rodové linie roste stejně rychle jako její střední hodnota.

Příklad 4.3. Uvažujme rod, v němž každý dospělý muž má s pravděpodobností syna, který se dožije dospělosti, má dva takové syny s pravděpodobností a s pravděpodobností se žádný z jeho synů dospělosti nedožije; přitom Určete pravděpodobnost, že tento rod dlouhodobě přežívá. Dále vypočítejte očekávaný počet mužských příslušníků tohoto rodu a jeho směrodatnou odchylku.

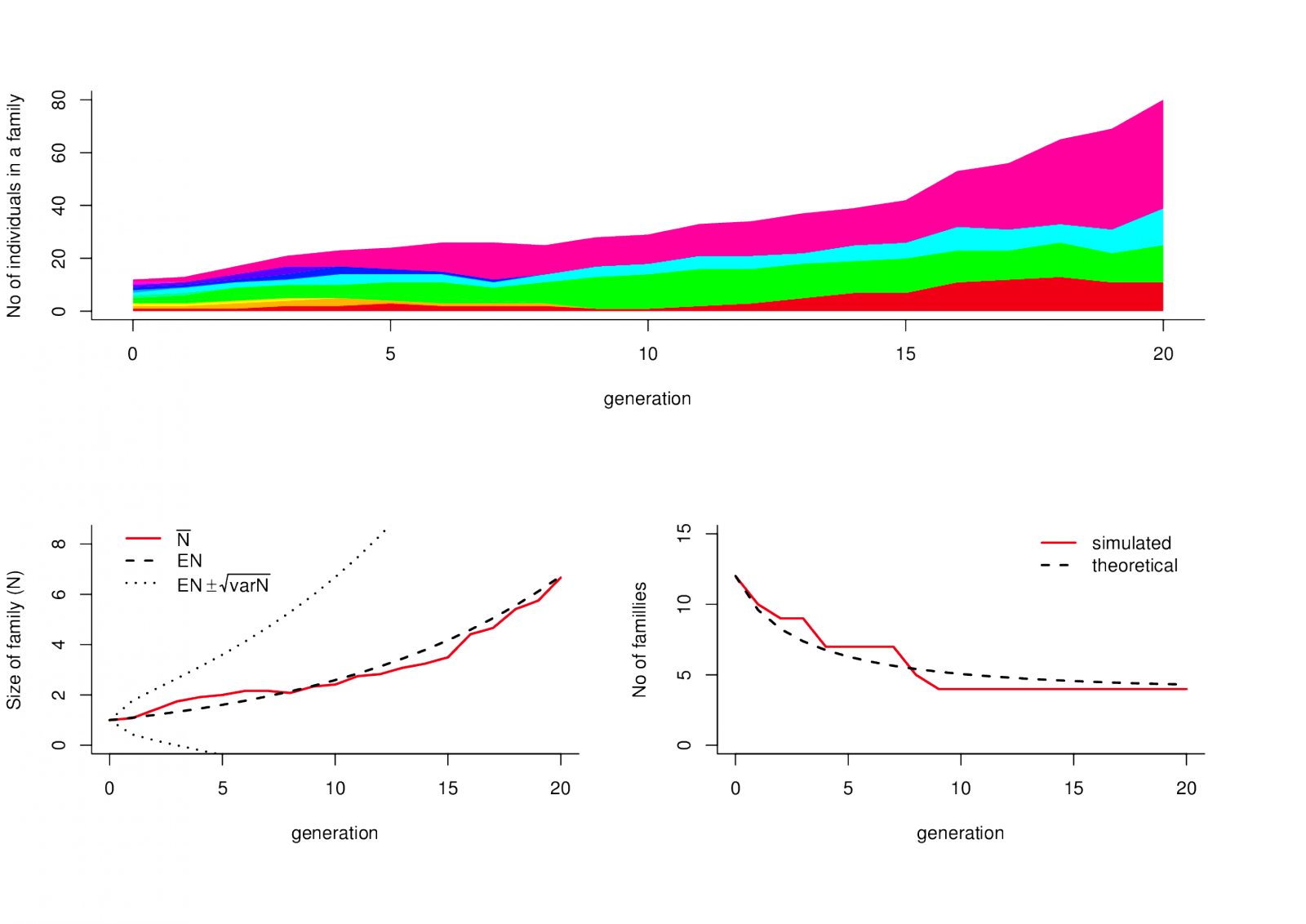
Obr. 6. Ilustrace výsledků Příkladu 4.3. Simulace vývoje dvaceti generací populace, kterou založilo N(0)=12 rodin. Přitom ve všech rodinách jsou stejné pravděpodobnost, že žádný syn se nedožije dospělosti , že se právě jeden dožije dospělosti a že se právě dva synové dožijí dospělosti . Nahoře: Počet mužských příslušníků populace v jednotlivých generacích; každé rodině odpovídá jedna barva. Po dvaceti generacích přežívají čtyři rodiny. Dole vlevo: Vývoj velikosti N(t) jedné rodiny. Černá čárkovaná čára vyjadřuje očekávanou velikost rodiny černá tečkovaná čára vyjadřuje rozpětí směrodatné odchylky velikosti rodiny v jednotlivých generacích kolem její střední hodnoty Červená plná čára je průměr ze simulovaných velikostí rodin. Dole vpravo: Počet rodin v populaci v jednotlivých generací. Červená čára je počet simulovaných rodin s nenulovou velikostí (přežívajících), černá čárkovaná čára vyjadřuje teoretický počet x(t)N(t) přežívajících rodin.

Střední počet synů, kteří se v takovém rodu dožijí dospělosti, je

Pokud tedy tj. neboli pak rod vymře jistě. Nechť nyní

Pravděpodobnost že takový rod vymře nejpozději v -té generaci, je dána rekurentně rovnostmi Aplikace (93), Aplikace (88). V našem konkrétním případě je takže posloupnost je řešením autonomní diferenční rovnice

Rovnovážné body této rovnice jsou řešením (algebraické) kvadratické rovnice

tedy

Podle předpokladu odtud plyne, že

Celkem můžeme uzavřít, že pravděpodobnost dlouhodobého přežití rodu je rovna

Náhodná veličina vyjadřující počet synů, kteří se dožijí dospělosti, má střední hodnotu

a rozptyl

Očekávaný počet mužských příslušníků rodu v -té generaci je tedy podle Aplikace (107) roven

a jeho směrodatná odchylka je podle Aplikace (110) rovna

Volme konkrétně a Pak je střední hodnota počtu potomků pravděpodobnost vyhynutí rodové linie a pravděpodobnost jejího dlouhodobého přežití Velikost populace tvořená takovými rodovými liniemi tedy bude pomalu růst (jako geometrická posloupnost s kvocientem 1,1) a dlouhodobě v ní bude přežívat asi třetina rodin zakladatelů. Na obr. Aplikace 6 jsou výsledky jedné simulace vývoje populace, kterou založilo 12 rodin; tyto výsledky jsou v dobrém souladu s rozvíjenou teorií.

Ještě si můžeme všimnout, že situace popsaná v příkladu 1 je speciálním případem situace popisované nyní; stačí položit

¹Viz např. A. Rényi. Teorie pravděpodobnosti. Praha, Academia 1972, str. 126-128.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity