Rovnice s konstantními koeficienty a speciální pravou stranou

Uvažujme nehomogenní lineární diferenční rovnici -tého řádu druhého typu

(46)

a k ní přidruženou lineární homogenní rovnici Lineární rovnice (36). Označme polynomiální operátor posunu z levé strany operátorové rovnice Lineární rovnice (37) symbolem homogenní rovnici Lineární rovnice (36) tedy můžeme zapsat ve tvaru

a nehomogenní rovnici ve tvaru

Definice 3.10.  Nechť je posloupnost, jsou konstanty takové, že a nechť je polynomiální operátor posunu, Řekneme, že operátor je anihilátor posloupnosti pokud

Podle této terminologie je anihilátorem každého řešení homogenní rovnice Lineární rovnice (36).

Nechť existuje anihilátor posloupnosti která je na pravé straně nehomogenní rovnice Lineární rovnice (46). To znamená, že je řešením nějaké lineární homogenní rovnice s konstatntními koeficienty, takže podle důsledku Lineární rovnice 3.7 je posloupnost lineární kombinací výrazů Nechť dále je řešením nehomogenní rovnice Lineární rovnice (46). Pak platí

(47)

To znamená, že řešení nehomogenní lineární rovnice -tého řádu je současně řešením lineární rovnice -tého řádu.

Nechť jsou charakteristické kořeny homogenní rovnice

a jsou charakteristické kořeny homogenní rovnice

Nyní rozlišíme dva případy.

Případ 1: V tomto případě můžeme psát řešení nehomogenní rovnice podle tabulky Lineární rovnice 2. Takové obecně zapsané řešení dosadíme do rovnice Lineární rovnice (46) a vypočítáme konstanty

Tab. 2. Tvary řešení nehomogenní rovnice Lineární rovnice (46) pro různé pravé strany b.

Případ 2: V tomto případě nejprve najdeme obecné řešení homogenní rovnice Lineární rovnice (46) a vynecháme v něm všechny členy, které se vyskytují v obecném řešení přidružené homogenní rovnice Lineární rovnice (36). Tím dostaneme řešení nehomogenní rovnice Lineární rovnice (46) s neurčitými koeficienty, které určíme dosazením do původní rovnice Lineární rovnice (46).

Příklad 3.11. Najdeme obecné řešení nehomogenní rovnice druhého řádu

(48)

Charakteristická rovnice přidružené homogenní rovnice

má množina charakteristických kořenů její obecné řešení je proto posloupnost daná předpisem

Anihilátor řešení přidružené homogenní rovnice je polynomiální operátor posunu

(koeficienty v operátoru jsou stejné, jako koeficienty v charakteristickém polynomu).

Pravá strana dané rovnice je řešením lineární homogenní rovnice, která má trojnásobný charakteristický kořen Nejjednodušší taková algebraická rovnice je Posloupnost na pravé straně rovnice Lineární rovnice (48) je tedy řešením lineární homogenní diferenční rovnice

(49)

její anihilátor je

Množina charakteristických kořenů rovnice Lineární rovnice (49) je jednoprvková To znamená, že tj. nastává Případ 2.

Posloupnost na levé straně relace Lineární rovnice (47) je v tomto konkrétním případě dána výrazem

Homogenní rovnice

(50)

má charakteristickou rovnmici

po úpravě

Tato rovnice má jednoduchý kořen a čtyřnásobný kořen obecné řešení homogenní rovnice Lineární rovnice (50) tedy je posloupnost daná předpisem

(51)

Vynecháním členů, které se vyskytují v obecném řešení přidružené homogenní rovnice k rovnici zadané dostaneme řešení nehomogenní rovnice Lineární rovnice (50) ve tvaru s neurčitými koeficienty

které určíme dosazením do dané rovnice:

Porovnáním koeficientů dostaneme soustavu lineárních algebraických rovnic

která má řešení Celkem dostáváme obecné řešení rovnice Lineární rovnice (48) ve tvaru

Ještě poznamenejme, že uvedený postup měl především ilustrovat obecnou teorii. Pro praktické počítání je příliš zdlouhavý; zejména vyjadřování příslušných anihilátorů není pro nalezení výsledků nutné. Bezprostředně lze totiž psát, že řešení nehomogenní rovnice Lineární rovnice (48) je řešením lineární homogenní rovnice pátého řádu, jejíž charakteristická rovnice je tvaru

Poté napíšeme obecné řešení takové rovnice - což je posloupnost Lineární rovnice (51), dosadíme do rovnice zadané a tak určíme tři z pěti konstant obecného řešení.

Stručně lze říci, že „speciální pravá strana rovnice Lineární rovnice (46)“ je taková posloupnost která je řešením nějaké lineární homogenní rovnice. V takovém případě vezmeme všechny charakteristické kořeny rovnice, jejímž řešením posloupnost je (ty jsou vidět již z tvaru posloupnosti podle důsledků Lineární rovnice 3.6 -Lineární rovnice 3.8 věty Lineární rovnice 3.5), a všechny charakteristické kořeny lineární homogenní rovnice přidružené k rovnici Lineární rovnice (46); kořeny bereme včetně násobností. Napíšeme obecné řešení homogenní rovnice odpovídající všem těmto charakteristickým kořenům, dosadíme ho do dané rovnice a určíme všechny konstanty, které určit lze.

Příklad 3.12. Najdeme obecné řešení rovnice

Charakteristická rovnice přidružené homogenní rovnice

má komplexně sdružené kořeny Posloupnost na pravé straně dané rovnice je řešením lineární homogenní rovnice, která má dvojnásobný kořen  abychom zůstali v reálném oboru, vezmeme dvojici komplexně sdružených dvojnásobných kořenů Máme tedy celkem trojnásobné komplexně sdružené kořeny a obecný tvar řešení

Tuto posloupnost dosadíme do dané rovnice. Poněvadž

dostaneme

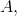
Porovnáním koeficientů dostáváme tedy a koeficienty zůstávají neurčené. Obecné řešení dané rovnice je dáno výrazem

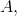
kde jsou konstanty.

Pro nehomogenní lineární diferenční rovnice tvaru Lineární rovnice (46) s pravou stranou ve tvaru polynomu můžeme zformulovat ještě jednodušší pravidlo pro hledání řešení: Nechť je stupeň polynomu na pravé straně rovnice Lineární rovnice (46) a je násobnost charakteristického kořene přidružené homogenní rovnice (samozřejmě, že může být pokud charakteristická rovnice nemá kořen 1). Pak řešení nehomogenní rovnice je tvaru polynomu stupně