Mizení rodové linie

Uvažujme populaci s nepřekrývajícími se generacemi. Její vývoj si budeme představovat tak, že každá generace žije jedno časové období a „vyprodukuje“ generaci bezprostředních potomků. Všechny jedince budeme považovat za identické. Zejména to znamená, že počet bezprostředních potomků nějakého jedince nezávisí na tom, zda tento jedinec měl či neměl nějaké sourozence a kolik jich bylo. Potomky jednoho jedince (kterému budeme říkat „zakladatel rodu“) všech generací nazveme rodová linie; sám „zakladatel rodu“ do rodové linie samozřejmě patří.

Zavedeme náhodnou veličinu vyjadřující počet bezprostředních potomků jedince; jedná se o veličinu diskrétní. Označme pravděpodobnost, že jedinec má právě bezprostředních potomků; tedy představují hodnoty pravděpodobnostní funkce náhodné veličiny Tyto hodnoty splňují nerovnosti pro všechna a platí

(86)

Dále budeme předpokládat, že bezprostřední vyhynutí linie je možné, ale není jisté, tedy že

Očekávaný počet bezprostředních potomků jedince, tedy střední hodnota náhodné veličiny je dána součtem

(87)

Označme pravděpodobnost, že rodová linie vymře nejpozději v čase tj. nejpozději v -té generaci. Za nultou generaci budeme považovat „zakladatele rodu“. Ten samozřejmě žil, takže jeho linie v nulté generaci nevymřela, tj.

(88)

Extinkce potomků v první generaci znamená, že jedinec nemá žádné bezprostřední potomky, tj. Pravděpodobnost, že linie vymře do druhé generace, je pravděpodobnost vzájemně neslučitelných jevů, že jedinec nemá bezprostředního potomka, nebo že jedinec má jednoho bezprostředního potomka, který bezprostřední potomky již nemá, nebo že jedinec má dva bezprostřední potomky a z nich každý zemře bez bezprostředních potomků, atd. Tedy

Podobně

a obecně

(89)

Nyní zavedeme reálnou funkci jako součet mocninné řady¹

(90)

Podle podmínky Aplikace (86) je poloměr konvergence této řady alespoň 1 a platí

(91)

Dále a

(92)

Odtud plyne, že pro je a což znamená, že funkce je neklesající a konvexní na intervalu

Pravděpodobnost vymření linie nejpozději v -té generaci je podle vyjádření Aplikace (89) řešením nelineární autonomní rekurentní formule prvního řádu

(93)

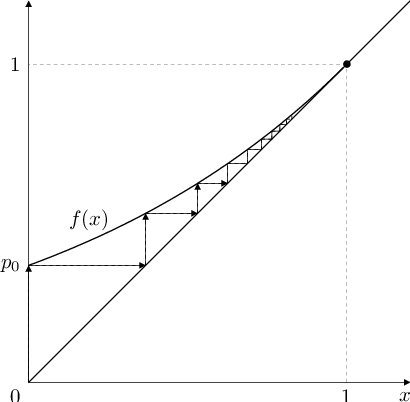
s počáteční podmínkou Aplikace (88). Poněvadž již známe průběh funkce  můžeme kvalitativní vlastnosti řešení úlohy Aplikace (93), Aplikace (88) vyšetřit graficky. Mohou nastat dva případy, viz obr. Aplikace 5.

Obr. 5. Graficé řešení počáteční úlohy Aplikace (93), Aplikace (88) v případě (vlevo) a (vpravo).

Pokud pak graf funkce na intervalu leží nad osou prvního kvadrantu. To znamená, že rovnice Aplikace (93) má jediné rovnovážné řešení který je asymptoticky stabilní. Pro řešení úlohy Aplikace (93), Aplikace (88) pak platí

Tedy pravděpodobnost, že linie někdy v budoucnu vymře, se blíží jistotě.

Pokud pak má graf funkce uvnitř intervalu jeden průsečík s osou prvního kvadrantu. Existuje tedy hodnota která je asymptoticky stabilním rovnovážným bodem rovnice Aplikace (93). Pro řešení úlohy Aplikace (93), Aplikace (88) platí

To znamená, že pravděpodobnost vymření linie dosáhne nějaké nenulové hodnoty.

Porovnáním první rovnosti v Aplikace (92) s formulí Aplikace (87) vidíme, že

(94)

Dosažený výsledek tedy můžeme interpretovat následujícím způsobem. Pokud střední hodnota počtu bezprostředních potomků jedince nepřesáhne 1, pak rodová linie jistě vymře; to byl očekávatelný výsledek. Ale i v případě, že střední počet bezprostředních potomků každého jedince je větší než 1, existuje nenulová pravděpodobnost, že rodová linie z populace vymizí.

Příklad 4.1. Uvažujme hypotetické buňky, které se řídí následujícím pravidlem: za časovou jednotku buňka buď uhyne, nebo se rozdělí na dvě identické; pravděpodobnost obou těchto jevů je stejná. Do živného roztoku na počátku vložíme jednu takovou buňku. Určete pravděpodobnost, že kolonie buněk vzniklých tímto způsobem bude žít ještě v čase

(Promyslete si, že úloha je ekvivalentní s úlohou o přežívání rodiny, v níž se se dospělosti dožijí buď dva synové anebo žádný, přičemž každá z těchto možností nastane s pravděpodobností ; to je úloha, kterou v první polovině 19. století řešil I. J. Bienaymé.)

V tomto případě je Funkce definovaná rovností Aplikace (90) má tvar

Pravděpodobnost , že kolonie buněk vyhyne nejpozději v čase , je řešením počáteční úlohy Aplikace (93), Aplikace (88), tedy v našem případě

(95)

S pomocí libovolného software, úplně stačí nějaký tabulkový procesor, můžeme vypočítat Hledaná pravděpodobnost, že kolonie v čase ještě žije, je rovna

Dále, střední hodnota náhodné veličiny vyjadřující počet potomků jedné buňky je

což souhlasí s vyjádřením podle Aplikace (91). Posloupnost definovaná rekurentně vztahy Aplikace (95) má tedy limitu

V průběhu výpočtu jsme si mohli všimnout, že konvergence posloupnosti je velice pomalá a ze znalosti prvních 35 členů nelze na první pohled určit, zda posloupnost konverguje; a pokud ano, tak k jaké hodnotě.

Příklad 4.2. Uvažujme rostlinu, která vyprodukuje semen a každé z nich má pravděpodobnost že z něj vyroste nová rostlina. Určete pravděpodobnost, že potomci jedné rostliny z populace vymizí.

Pravděpodobnost , že rostlina bude mít potomků, je pravděpodobnostní funkcí binomického rozdělení,

Funkce definovaná mocninnou řadou Aplikace (90) má tvar

takže a Pokud tedy pak potomci rostliny z populace jistě vymizí; pochopitelně, v takovém případě je totiž střední počet potomků jedné rostliny menší než 1.

Nechť Pak pravděpodobnost že potomci rostliny vymizí nejpozději v -té generaci je podle Aplikace (93) a Aplikace (88) řešením počáteční úlohy

(96)

Spočítejme například prvních deset členů této posloupnosti pro a

Tento výpočet uvedli Galton a Watson v článku zmíněném v Problém extinkce a chybně z něho usoudili, že posloupnost pomalu konverguje k 1. Uvažovaná diferenční rovnice má však kromě rovnovážného bodu 1 také rovnovážný bod mezi 0 a 1, který je řešením algebraické rovnice

a k němuž konverguje řešení úlohy Aplikace (96); pro hodnoty a je

¹Funkce je vytvořující funkcí diskrétní náhodné veličiny Některé z následujících odvozovaných výsledků jsou speciálními případy obecné teorie vytvořujících funkcí.