Grafické řešení
Uvažujme nelineární diferenční rovnici (rekurentní formuli) prvního řádu Autonomní rovnice (6) s počáteční podmínkou Autonomní rovnice (7). Rovnici lze chápat také jako zápis zobrazení, které reálné hodnotě přiřadí hodnotu
tj. jako reálnou funkci jedné reálné proměnné. Toto zobrazení lze znázornit v souřadné rovině - na vodorovnou osu nanášíme hodnoty
na svislou hodnoty
Nakreslíme tedy graf funkce
a pro danou hodnotu
na něm najdeme hodnotu
Stejným způsobem chceme najít hodnotu pomocí hodnoty
Hodnotu
tedy přeneseme na vodorovnou osu; to můžeme udělat tak, že sestrojíme vodorovnou úsečku ve výšce
(„výškou“ rozumím, že přímka incidentní s touto úsečkou prochází bodem
na svislé ose) a najdeme její průsečík s osou prvního kvadrantu, tedy bod
Nyní průsečík svislé přímky procházející tímto bodem a grafu funkce
má druhou souřadnici rovnu hledané hodnotě
 |
 |
 |
 |
|
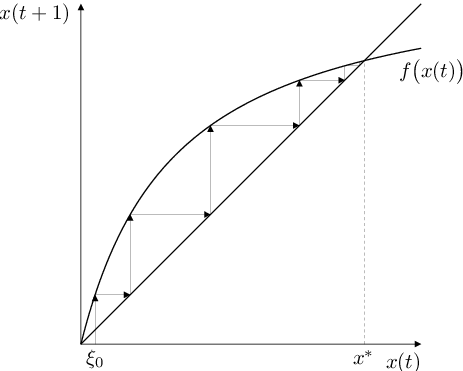
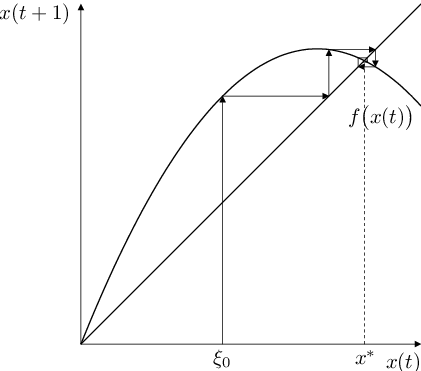
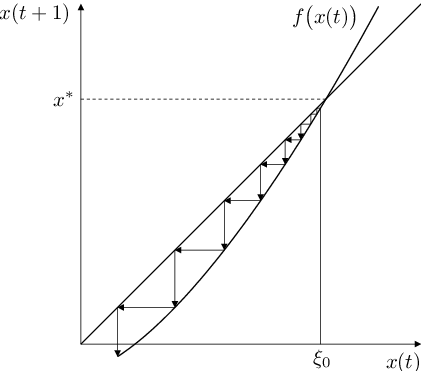
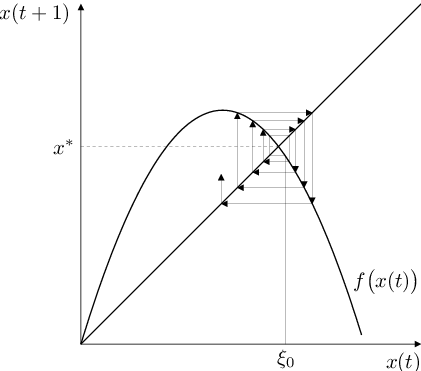
Obr. 1. Grafické řešení autonomní rovnice Autonomní rovnice (6). Vlevo „schodový diagram“, vpravo „pavučinový diagram“, nahoře stabilní (přitahující) pevný (rovnovážný) bod zobrazení f, dole nestabilní (odpuzující).
|
|
Při hledání hodnoty řešení uvažované diferenční rovnice tedy sestrojíme vodorovnou úsečku s krajními body
a
poté úsečku s krajními body
a
Tímto způsobem můžeme pokračovat a postupně nacházet (konstruovat) jednotlivé členy posloupnosti, která řeší danou diferenční rovnici. V závislosti na tvaru grafu funkce
úsečky konstruované popsaným způsobem vytváří „schody“, obr. Autonomní rovnice 1 vlevo, (odtud používaný název „stair step diagram“) nebo „pavučinu“ („codweb diagram“), obr. Autonomní rovnice 1 vpravo.
Pokud je funkce konkávní, má nejvýše dva pevné body. To znamená, že existují nejvýše dvě hodnoty
takové, že
Tyto
body jsou souřadnicemi průsečíků grafu funkce a osy prvního kvadrantu. Na diagramech konstruovaných popsaným způsobem je dobře vidět, za jakých podmínek (tj. při jakém tvaru funkce
) se řešení uvažované diferenční rovnice od stacionárního bodu vzdaluje (obr. Autonomní rovnice 1 dole) nebo se k němu přibližuje (obr. Autonomní rovnice 1 nahoře).
Příklad 2.4. Procedura grafického řešení diferenční rovnice je na animovaných obrázcích ilustrována pro rovnici s funkcí
danou předpisem
tj. pro rovnici
(8) což je speciální případ Rickerova modelu Přípravné úvahy (17) vývoje velikosti populace s nepřekrývajícími se generacemi; kapacitu prostředí přitom považujeme za jednotkovou. V závislosti na velikosti růstového koeficientu
může řešení monotonně konvergovat k hodnotě
(na obr. Autonomní rovnice 2 pro
), konvergovat k ní s tlumenými oscilacemi (na obr. Autonomní rovnice 3 pro
), periodicky kolem ní kolísat (na obr. Autonomní rovnice 4 pro
je perioda rovna 4), nebo kolísat nepravidelně, chaoticky (na obr. Autonomní rovnice 5 pro
).
| Animace 5 - pocatecni uloha linearni rovnice.pdf |
|
Obr. 2. Ilustrace řešení diferenční rovnice Autonomní rovnice (8) s r=1,5. V levé části obrázku je „schodovitá procedura“ konstrukce řešení, v pravé části obrázku je výsledné řešení rovnice zobrazené jako hodnoty závislé na čase.
|
|
Animace 6 - ilustrace reseni diferencni rovnice.pdf |
|
Obr. 3. Ilustrace řešení diferenční rovnice Autonomní rovnice (8) s r=6. V levé části obrázku je „pavučinová procedura“ konstrukce řešení, v pravé části obrázku je výsledné řešení rovnice zobrazené jako hodnoty závislé na čase.
|
| Animace 7 - ilustrace reseni diferencni rovnice 2.pdf |
|
Obr. 4. Ilustrace řešení diferenční rovnice Autonomní rovnice (8) s r=14. V levé části obrázku je „pavučinová procedura“ konstrukce řešení, v pravé části obrázku je výsledné řešení rovnice zobrazené jako hodnoty závislé na čase.
|
| Animace 8 - ilustrace reseni diferencni rovnice 3.pdf |
|
Obr. 5. Ilustrace řešení diferenční rovnice Autonomní rovnice (8) s r=50. V levé části obrázku je „pavučinová procedura“ konstrukce řešení, v pravé části obrázku je výsledné řešení rovnice zobrazené jako
hodnoty závislé na čase.
|
| Název | Zadal | |
|---|---|---|
 Animace 5 - pocatecni uloha linearni rovnice (vytvořeno: 28. 6. 2015) | doc. RNDr. Zdeněk Pospíšil, Dr | 167,42 kB |
| Animace 6 - ilustrace reseni diferencni rovnice (vytvořeno: 28. 6. 2015) | doc. RNDr. Zdeněk Pospíšil, Dr | 310,08 kB |
| Animace 7 - ilustrace reseni diferencni rovnice 2 (vytvořeno: 28. 6. 2015) | doc. RNDr. Zdeněk Pospíšil, Dr | 287,31 kB |
| Animace 8 - ilustrace reseni diferencni rovnice 3 (vytvořeno: 28. 6. 2015) | doc. RNDr. Zdeněk Pospíšil, Dr | 282,74 kB |
