Definice 2.1. Reálná posloupnost je zobrazení z množiny celých čísel do množiny reálných čísel takové, že jeho definiční obor je celá množina nebo některá z množin

Přívlastek „reálná“ budeme většinou vynechávat. Hodnotu posloupnosti budeme nazývat člen posloupnosti nebo podrobněji -tý člen posloupnosti. Hodnotu nezávisle proměnné budeme někdy nazývat index posloupnosti. Pokud a řekneme, že je počáteční index posloupnosti.

Posloupnost můžeme také zapisovat pomocí jejích členů jako nebo stručně

Množinu posloupností definovaných na resp. na , označíme symbolem resp. $; množinu všech posloupností označíme symbolem , tj.

Tvrzení 2.2. Buď Množina posloupností je vektorovým prostorem nad polem reálných čísel . Sčítání posloupností je definováno vztahem

nulovým prvkem je posloupnost taková, že tj.

násobení skalárem je definováno vztahem

Věta 2.3. Nechť . Označme

Pokud existuje takový index, že pak jsou posloupnosti lineárně nezávislé.

Jsou-li posloupnosti lineárně závislé, pak pro všechny indexy

Důkaz. Nechť pro konstanty platí

a nechť je takový index, že Z předchozí rovnosti nyní plyne

To je homogenní soustava lineárních rovnic pro neznámých a je její determinant. Odtud plyne, že tato soustava má jen triviální řešení, tj.

To ovšem znamená, že posloupnosti jsou lineárně nezávislé a první tvrzení je dokázáno.

Druhé tvrzení je bezprostředním důsledkem prvního.

Poznámka 2.4. Determinant zavedený v předchozí větě se nazývá Casoratián posloupností v indexu Tvrzení Přípravné úvahy 2.3 lze tedy přeformulovat: Jsou-li posloupnosti lineárně závislé, pak jejich Casoratián je nulový v každém indexu ze společného definičního oboru těchto posloupností.

Definice 2.5. Posloupnost se nazývá

ohraničená zdola, pokud existuje nějaká hranice taková, že žádný člen posloupnosti není menší než tato hranice, tj.

ohraničená shora, pokud existuje nějaká hranice taková, že žádný člen posloupnosti není větší než tato hranice, tj.

ohraničená, pokud je ohraničená zdola i shora, tj.

Definice 2.6. Posloupnost se nazývá

rostoucí, pokud pro každou hodnotu argumentu platí nerovnost tj.

ryze rostoucí, pokud pro každou hodnotu argumentu platí nerovnost tj.

klesající, pokud pro každou hodnotu argumentu platí nerovnost tj.

ryze klesající, pokud pro každou hodnotu argumentu platí nerovnost tj.

monotonní, pokud je rostoucí nebo klesající;
ryze monotonní, pokud je ryze rostoucí nebo ryze klesající;
stacionární, pokud je současně rostoucí a klesající.

Terminologická poznámka. Uvedená terminologie monotonních posloupností je méně obvyklá - posloupnost splňující podmínku

je častěji nazývaná „neklesající“ a posloupnost splňující podmínku

„rostoucí“, podobně pro posloupnosti klesající. V této tradičnější terminologii však posloupnost, která není „klesající“ ještě nemusí být „neklesající“ (např. posloupnost daná rovností ).

V terminologii zavedené v definici Přípravné úvahy 2.5 je ryze rostoucí posloupnost také posloupností rostoucí; pojem označující zvláštní případ nějakého obecnějšího pojmu se od tohoto obecnějšího pojmu liší přívlastkem (vpojetí aristotelské logiky nebo biologické klasifikace lze slovo „rostoucí“ považovat za rodové jméno, slovo „ryze“ za druhové jméno).¹

Poznámka 2.7. Z tranzitivity relací plyne, že posloupnost je

rostoucí právě tehdy, když

ryze rostoucí právě tehdy, když

klesající právě tehdy, když

ryze klesající právě tehdy, když

Poznámka 2.8. Obor hodnot stacionární posloupnosti je jednoprvkový, tj. existuje takové, že a

Je-li stacionární posloupnost a budeme psát . S použitím této symboliky můžeme nulovou posloupnost zapsat jako

Poznámka 2.9. Všechny pojmy zavedené v definici Přípravné úvahy 2.6 lze relativizovat na interval nezávisle proměnné. Např. posloupnost se nazývá klesající na intervalu jestliže pro každý index posloupnosti takový, že platí tj.

Definice 2.10. Buď a Řekneme, že index je

uzel posloupnosti pokud nebo
argument lokálního maxima, pokud a
argument lokálního minima, pokud a
argument ostrého lokálního maxima, pokud a
argument ostrého lokálního minima, pokud a

argument lokálního extrému, pokud je argumentem lokálního maxima nebo minima;
argument ostrého lokálního extrému, pokud je argumentem ostrého lokálního maxima nebo minima.

Je-li argumentem lokálního extrému, řekneme že hodnota je lokálním extrémem posloupnosti Analogickou terminologii používáme pro ostré lokální extrémy, maxima a minima.

Definice 2.11. Limita posloupnosti je zobrazení z množiny posloupností do rozšířené množiny reálných čísel Obraz posloupnosti při zobrazení značíme Řekneme, že limita posloupnosti je rovna hodnotě pokud ke každému okolí existuje takový index posloupnosti že všechny členy posloupnosti s indexy alespoň jsou v tomto okolí, tj.

Limita se nazývá vlastní, pokud tj.

Limita se nazývá nevlastní, pokud tj.

Posloupnost se nazývá konvergentní, pokud existuje Posloupnost se nazývá divergentní, pokud nebo

Terminologická poznámka. Nevlastní limita posloupnosti obvykle v učebních textech o posloupnostech nebývá považována za limitu; „nevlastní limita není limita analogicky jako nevlastní matka není matka“. Terminologie zavedená v definici Přípravné úvahy 2.11 je však stejná jako terminologie používaná v textech o funkcích.

Věta 2.12. Monotonní posloupnost má limitu. Podrobněji:

je-li rostoucí neohraničená posloupnost, pak
je-li rostoucí posloupnost ohraničená shora, pak
je-li klesající posloupnost ohraničená zdola, pak
je-li klesající neohraničená posloupnost, pak

Důkaz. V. Novák. Diferenciální počet v R. Brno, MU, 1997. Věta 5.5., str. 127.

Důsledek 2.13. Nechť je ryze rostoucí posloupnost taková, že Pak

Důkaz. Poněvadž je ryze rostoucí a pro každé je

Nechť je libovolné číslo. K němu existuje že Pro tento index platí

To znamená, že posloupnost není ohraničená shora a dokazované tvrzení plyne z věty Přípravné úvahy 2.12.

Tvrzení 2.14. Nechť Označme množinu konvergentních posloupností z vektorového prostoru tj.

Pak je vektorový podprostor prostoru a zobrazení je lineární.

Důkaz.

Definice 2.15. Nechť je libovolná posloupnost a je ryze rostoucí posloupnost celých čísel taková, že tj. Pak složené zobrazení se nazývá posloupnost vybraná z posloupnosti

Vzhledem k důsledku věty Přípravné úvahy 2.12 je složené zobrazení z předchozí definice skutečně posloupnost, -tý člen vybrané posloupnosti je

Tvrzení 2.16. Nechť je konvergentní nebo divergentní posloupnost. Pak je její limitou, tj. právě tehdy, když je limitou každé posloupnosti vybrané z posloupnosti

Důkaz. „“: Buď libovolné okolí limity a libovolná posloupnost vybraná z posloupnosti K okolí existuje takové, že pro všechna je Množina je podmnožinou dobře uspořádané množiny přirozených čísel, a tato množina je neprázdná, neboť Existuje tedy

Pro libovolné je a tedy

„“: Nechť Definujme vztahem Pak je posloupnost vybraná z posloupnosti Je tedy

Definice 2.17. Řekneme, že je hromadný bod posloupnosti pokud ke každému okolí a každému celému číslu existuje takový index posloupnosti který není menší než a člen posloupnosti leží v tomto okolí, tj.

Tvrzení 2.18. Hodnota je hromadným bodem posloupnosti právě tehdy, když existuje posloupnost vybraná z posloupnosti taková, že tj.

Důkaz. „“: Nechť je hromadným bodem posloupnosti Zkonstruujeme ryze rostoucí posloupnost takovou, že a

Buď libovolné okolí bodu a libovolný prvek.

Položíme K existuje že a

Položíme atd.

Výsledkem této induktivní konstrukce je ryze rostoucí posloupnost ; přitom a pro každý index a tedy Pro všechny indexy je což znamená, že

„“: Nechť existuje vybraná posloupnost taková, že Nechť je libovolné okolí a je libovolné číslo. Podle definice Přípravné úvahy 2.11 existuje číslo takové, že pro každé je Vezmeme takové, že a takové číslo existuje, neboť posloupnost je rostoucí a Položíme Pak a tedy je hromadným bodem posloupnosti

Tvrzení 2.19. Nechť existuje limita posloupnosti Pak je hromadným bodem posloupnosti

Důkaz. Plyne bezprostředně z tvrzení Přípravné úvahy 2.16 a Přípravné úvahy 2.18.

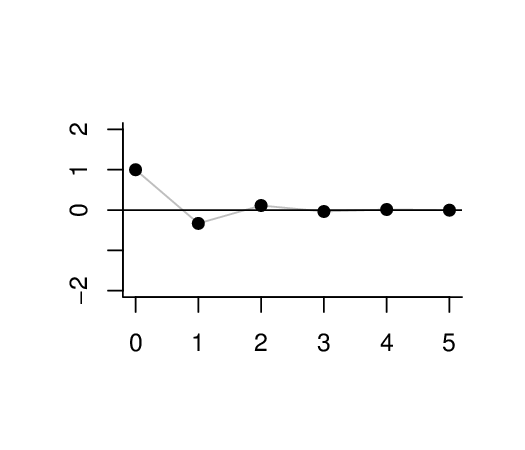
Příklad 2.20. Uvažujme posloupnosti z množiny

obr. Přípravné úvahy 5.a).
Jediný hromadný bod je 0.

obr. Přípravné úvahy 5.b).
Hromadné body jsou 1 a -1.

obr. Přípravné úvahy 5.c).
Hromadné body jsou 1 a -1.

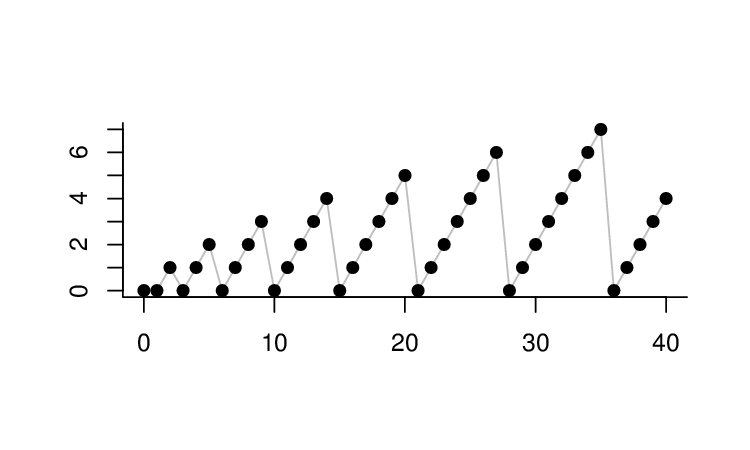
Definujme posloupnost předpisem kde označuje celou část z reálného čísla
Položme
obr. Přípravné úvahy 5.d).
Každé přirozené číslo se v této posloupnosti vyskytuje nekonečně mnohokrát, je tedy jejím hromadným bodem. Vybraná posloupnost

diverguje do je tedy také hromadným bodem posloupnosti

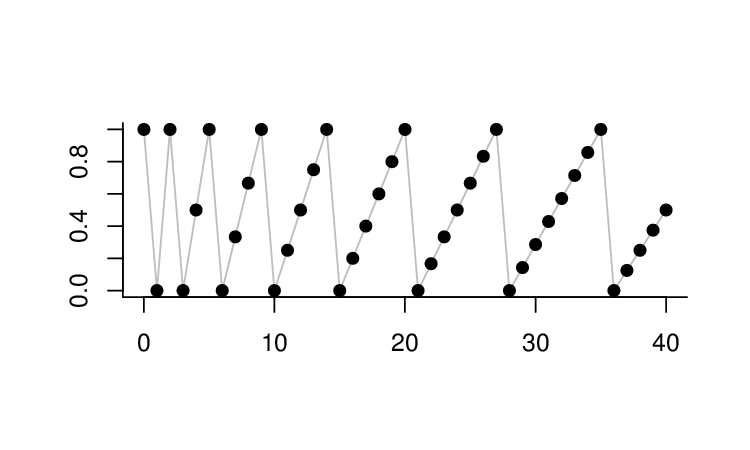
Uvažujme posloupnosti a zavedené v předchozím příkladu a položme

obr. Přípravné úvahy 5.e).
Každé racionální číslo z intervalu se mezi členy této posloupnosti vyskytuje nekonečně mnohokrát. V každém okolí libovolného reálného čísla z intervalu existuje nějaké racionální číslo To znamená, že každé reálné číslo z intervalu je hromadným bodem posloupnosti množina všech hromadných bodů vyplní kompaktní interval

Obr. 5. Příklady posloupností s různými množinami hromadných bodů.

Příklady ukazují, že posloupnost může mít jeden hromadný bod (a), konečně mnoho hromadných bodů (b, c), spočetně (d) nebo nespočetně (e) mnoho hromadných bodů; hromadný body mohou být konečné (a, b, c, e) nebo nekonečné (d); konečný hromadný bod může být členem posloupnosti (b, d, e) ale nemusí (a, c, e).

¹Analogická terminologie byla navržena v knize L. Kosmák. Základy matematickej analýzy. Bratislava-Praha, Alfa-SNTL, 1984, str. 16. Místo slova „ryze“ je tam používáno slovo „ostro“.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity


Obr. 5. Příklady posloupností s různými množinami hromadných bodů.