Berlínský akademik Johann Peter Süßmilch publikoval v roce 1741 pojednání Die göttliche Ordnung in der Veränderungen des menslichen Geschlechts aus der Geburt, dem Tode un der Fortpflanzung deßelben (Božský řád ve změnách lidských generací jejich rozením, smrtí a rozmnožováním), které je nyní považováno za první práci věnovanou demografii. Do jejího druhého vydání o dvacet let později zahrnul matematický model, který pro něj vypracoval Leonhard Euler. Model vychází z podobných zjednodušení jako Fibonacciův model růstu populace králíků, zahrnuje však vedle rození i umírání. Začíná v roce 0 s jedním lidským párem, přičemž muž i žena mají dvacet let. Euler dále předpokládal, že lidé umírají ve 40 letech, žení a vdávají se ve 20 letech a každý pár má šest dětí: dvě děti (chlapce a děvče) ve věku 22 let, další dva ve věku 24 let a poslední dvojici ve věku 26 let.

Vyjádříme Eulerův model formálně. Za jednotku času budeme považovat dva roky. Označíme

Novorozenci v čase jsou potomci párů 22-ti letých (tj. těch, kteří byli novorozenci před 22 lety, tedy v čase ), párů 24 letých a párů 26 letých. Pro veličinu tedy máme rekurentní vztah

Poněvadž lidé umírají ve 40 letech, je počet zemřelých párů v čase roven počtu novorozenců před 40 lety, tj.

(10)

V čase žijí páry, které žily v předchozím období a nezemřely, a dále páry, které se v tomto čase narodily. Platí tedy

Těmito úvahami dostáváme model vývoje populace tvořený třemi posloupnostmi, které splňují lineární diferenční rovnice

(11)

Vývoj modelované populace v prvních čtyřiceti letech, tj. v čase až je shrnut v tabulce Aplikace 3. V počátečním čase byl na Zemi pouze jeden pár dvacetiletých, tj. Po dvou letech k nim přibyli novorození chalapec a děvče, tj. Po dalších dvou letech přibyl další pár novorozenců, a po dalších dvou letech opět, Pak se čtrnáct let velikost populace neměnila, nikdo se nerodil ani neumíral. Za další dva roky, tj. 20 let od začátku prvotní pár zemřel, a za další dva roky přibyli první potomci prvního narozeného páru, Za další dva roky přibyli druzí dva potomci prvního narozeného páru a první dva potomci druhého narozeného páru, Tak můžeme v počítání pokračovat a dostaneme všechny počáteční podmínky pro vyšetřované rovnice, jak jsou uvedeny v tabulce Aplikace 3.

Tab. 3. Počáteční velikosti populace modelované rovnicemi Aplikace (11).

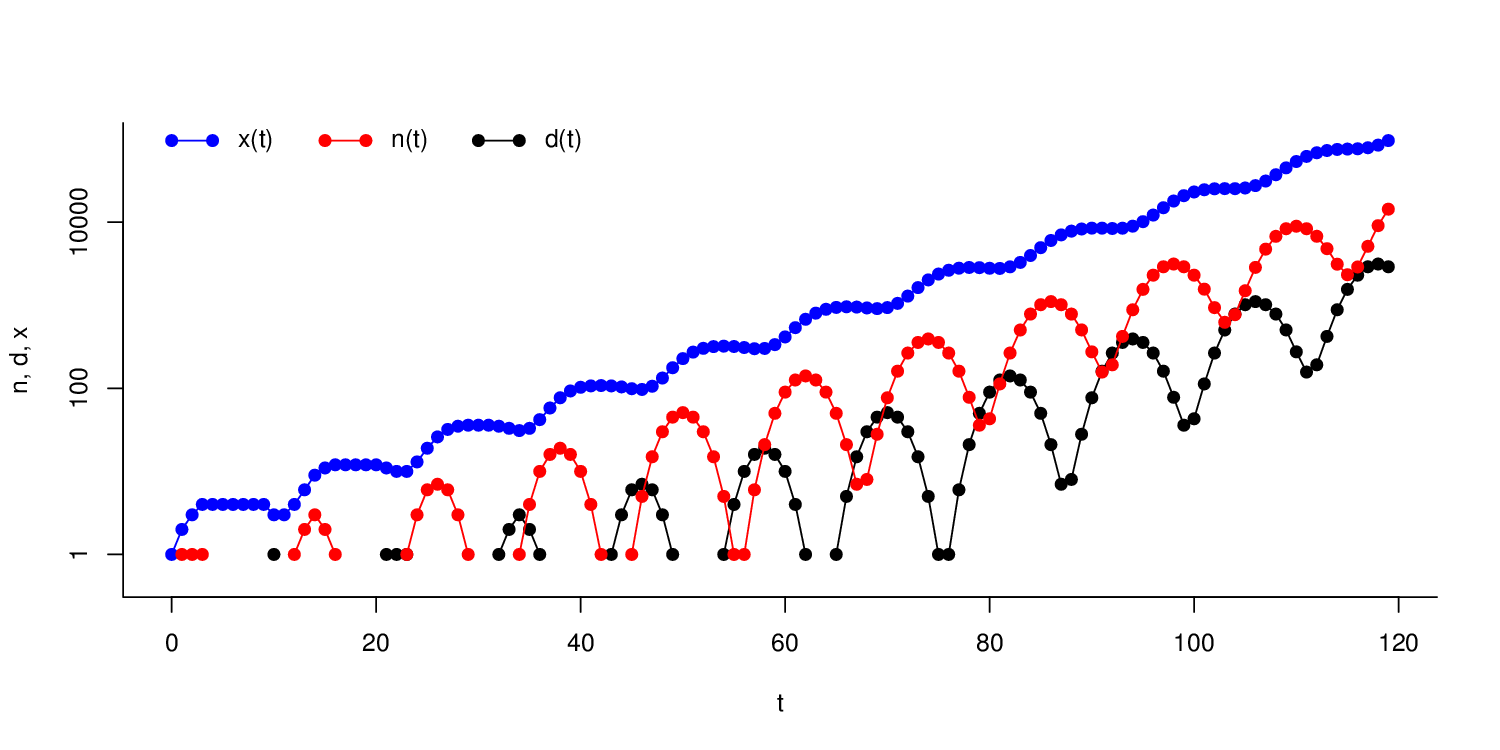
Obr. 1. Model „rozmnožování lidského rodu“ Aplikace (11). Na svislé ose je logaritmické měřítko. Symboly označují: x(t) - počet žijících párů v čase t, tj. 2t let od počátku, n(t) - počet narození v čase t, d(t) - počet úmrtí v čase t.

Uvedená rovnice spolu s počátečními podmínkami umožňují rekurentně počítat velikost populace v libovolném čase. L. Euler tento výpočet provedl až do času Na obrázku Aplikace 1 jsou zobrazeny hodnoty posloupností až do tohoto času. K problematice růstu populace se Euler později vrátil v rukopise Sur la multiplication du genre humain (O rozmnožování lidského rodu), který však za jeho života nevyšel. Tam odvodil (v 18. století, bez jakékoliv výpočetní techniky!), že velikost lidstva po dostatečně dlouhé době vývoje roste jako geometrická posloupnost s kvocientem což znamená, že jeho velikost se zdvojnásobí každých zhruba 15 let. Dále vztahem

ukázal, že počet úmrtí je zhruba šestkrát menší, než počet narození.

Vzhledem k podmínce Aplikace (10) můžeme původní Eulerův model Aplikace (11) zredukovat na dvě lineární diferenční rovnice

(12)

První z těchto rovnic je lineární homogenní diferenční rovnice pro posloupnost Můžeme ji tedy vyřešit metodami uvedenými v Homogenní rovnice s konstantními koeficienty a nalezenou posloupnost dosadit do druhé rovnice.

Charakteristická rovnice pro první z rovnic Aplikace (12) je

a má jeden reálný a 12 komplexně sdružených jednoduchých kořenů. Tyto kořeny jsou

Reálný charakteristický kořen je současně ryze dominantním charakteristickým kořenem. To znamená, že posloupnost je asymptoticky ekvivalentní s posloupností danou vztahem

Posloupnost lze proto považovat za první aproximaci posloupnosti Označíme

geometrickou posloupnost jednoduše vyjádříme vztahem a dosadíme ji do druhé z rovnic Aplikace (12). Tak najdeme první aproximaci posloupnosti Posloupnost tedy má splňovat

Budeme-li v této rovnosti psát místo dostaneme po jednoduché úpravě vyjádření diference posloupnosti ve tvaru

Podle Přípravné úvahy (25) a podle Diference a sumy některých posloupností tedy je

Vyjádření posloupnosti zjednodušíme tím, že označíme

(13)

Dostáváme tak první aproximace řešení systému diferenčních rovnic Aplikace (12) ve tvaru

(14)

Tyto posloupnosti lze považovat za vyjádření časového trendu množství novorozenců a velikosti populace.

Povšimněme si nyní toho, že pro argument charakteristických kořenů, které mají druhý největší modul, tj. kořenů platí

Odtud plyne, že „perioda kolísání“ posloupnosti kolem posloupnosti , tj. kolem jakési střední hodnoty počtu novorozených párů, je zhruba 12. Tento jev je také dobře pozorovatelný na obrázku Aplikace 1.

Označme pro stručnost Posloupnost daná vztahem

kde jsou vhodné konstanty určené počátečními podmínkami, „pro dostatečně velká dostatečně přesně aproximuje posloupnost “.

Nyní budeme hledat „dostatečně dobrou“ aproximaci posloupnosti Dostaneme ji tak, že ve druhé z rovnic Aplikace (12) budeme psát místo místo a místo Dostaneme

tedy

(15)

kde jsme označili

Z rovnice Aplikace (15) dostaneme aproximaci řešení druhé z rovnic Aplikace (12) ve tvaru

Toto vyjádření můžeme upravit s využitím Diference a sumy některých posloupností a označení Aplikace (13)

	(16)

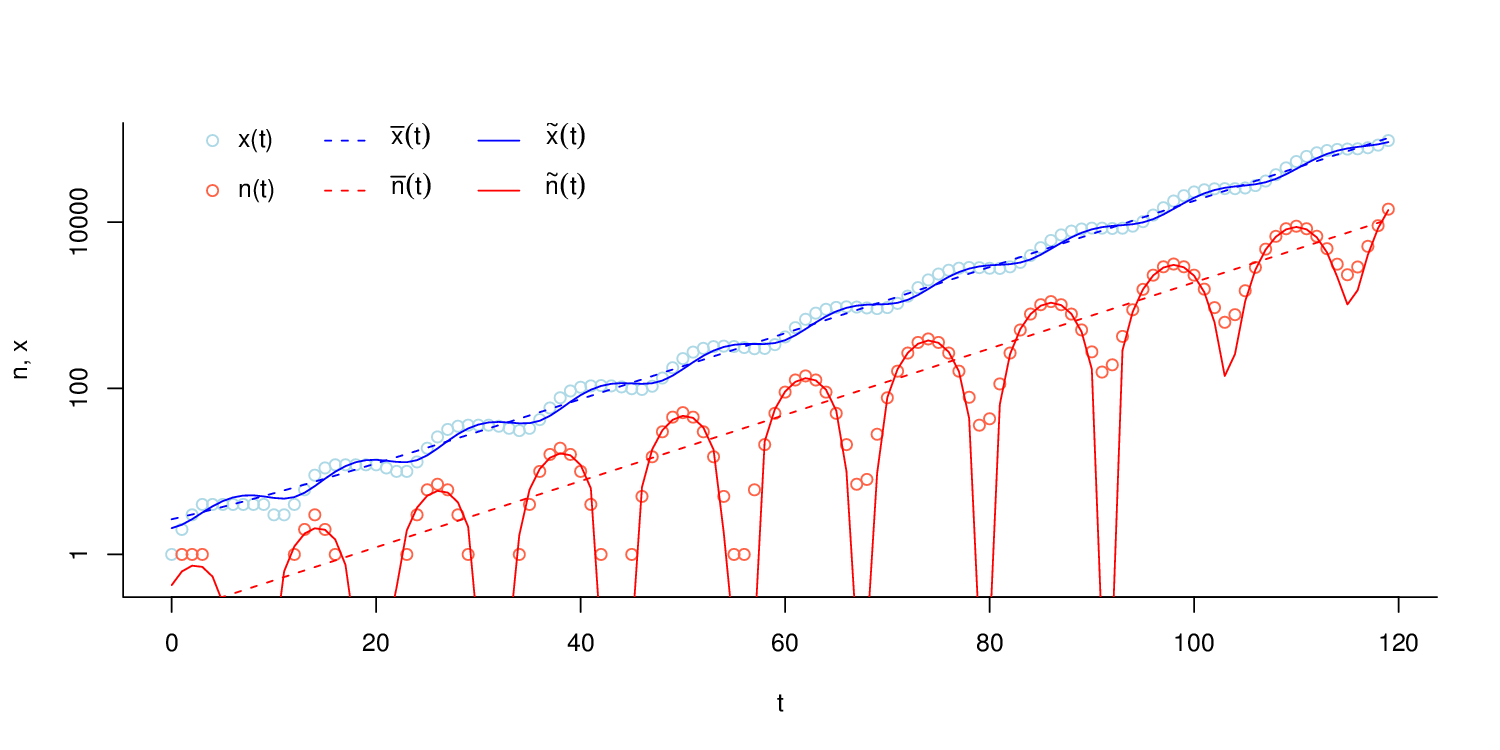
Aproximace Aplikace (14) a Aplikace (16) řešení systému Aplikace (12) jsou zobrazeny na obrázku Aplikace 2.

Obr. 2. Upravený model „rozmnožování lidského rodu“ Aplikace (12). Na svislé ose je logaritmické měřítko. Symboly označují: x(t), n(t) - hodnoty počítané z rekurentních vztahů Aplikace (12), - první aproximace řešení Aplikace (14) využívající pouze dominantní charakteristický kořen - druhá aproximace řešení Aplikace (16) využívající charakteristické kořeny s druhým největším modulem. Při výpočtu byly použity hodnoty

Model Aplikace (12) popisuje vývoj velikosti populace, která je strukturovaná do dvou tříd - novorozenci a ostatní. Snadno ho ale můžeme modifikovat, aby popisoval populaci strukturovanou podrobněji; může nás zajímat počet školních dětí, počet rodičů pečujících o děti předškolního věku a podobně. V Eulerově zjednodušení takové rozčlenění populace závisí pouze na věku jedinců. Označme proto počet párů věku (tj. let) v čase Pak platí

První z rovnic modelu Aplikace (12) nyní můžeme přepsat ve tvaru

Pro vývoj velikosti populace strukturované podle věku popsaným způsobem tak dostáváme model tvořený 21 lineárními diferenčními rovnicemi prvního řádu

(17)

Euler v podstatě předpokládal, že smrt je jistá ve čtyřiceti letech a v mladším věku je jisté přežití. Abychom model přiblížili realitě, nahradíme jistoty pravděpodobnostmi. Označme proto pravděpodobnost, že jedinec věku (tj. let) přežije jedno dvouleté období (tj. dožije se věku let). Dále nechť nejvyšší možný věk je let. Pak

Další Eulerův nerealistický předpoklad je ten, že dospělé páry mají v přesně daném věku právě jeden pár potomků. Tento předpoklad nahradíme realističtějším, že počet potomků páru věku je náhodná veličina se střední hodnotou První z rovnic modelu Aplikace (17) nyní můžeme nahradit rovnicí

hodnota posloupnosti nyní již nevyjadřuje počet novorozenců v čase ale očekávanou hodnotu tohoto počtu. Celkem tak dostáváme model tvořený lineárními diferenčními rovnicemi

Tento model můžeme zapsat ve vektorovém tvaru

nebo stručně

(18)

kde jsme označili

Maticový model Aplikace (18) poprvé zformuloval Patrick Holt Leslie ve slavném článku On the use of matrices in certain population mathematics, který publikoval roku 1945 v časopise Biometrika. Matice proto dostala název Leslieho matice.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity