Příklad: Rovnice druhého řádu.

Uvažujme lineární homogenní diferenční rovnici

(39)

s počátečními podmínkami

(40)

Aby rovnice Lineární rovnice (39) byla skutečně druhého řádu musí být O počátečních hodnotách a budeme předpokládat, že aspoň jedna z nich je nenulová. V opačném případě by totiž počáteční úloha Lineární rovnice (39), Lineární rovnice (40) měla jedině triviální řešení při libovolných hodnotách svých parametrů

Charakteristickou rovnicí je kvadratická rovnice pro neznámou

(41)

Mohou nastat tři případy.

• (i)

Charakteristická rovnice Lineární rovnice (41) má dva reálné různé kořeny Označení zvolíme tak, aby charakteristický kořen nazveme dominatní. Diferenční rovnice Lineární rovnice (39) má řešení

(42)

neboť

Konstanty a volíme tak, aby byly splňeny počáteční podmínky Lineární rovnice (40), tedy jako řešení soustavy lineárních (algebraických) rovnic

Determinant této soustavy je

což znamená, že soustava je jednoznačně řešitelná a že posloupnosti definované vztahy

tvoří fundamentální systém řešení lineární homogenní diferenční rovnice Lineární rovnice (39).

Posloupnost definovaná vztahem Lineární rovnice (42), kde konstanty jsou dány vztahy

je řešením počáteční úlohy Lineární rovnice (39), Lineární rovnice (40). Explicitněji můžeme řešení úlohy Lineární rovnice (39), Lineární rovnice (40) vyjádřit formulí

Pokud jsou počáteční podmínky takové, že můžeme řešení úlohy Lineární rovnice (39), Lineární rovnice (40) přepsat do tvaru

Nechť nejprve Pak

Odtud je vidět, že v případě „se pro velká  řešení úlohy Lineární rovnice (39), Lineární rovnice (40) chová jako geometrická posloupnost s kvocientem “ Chování řešení je tedy pro velká určeno dominantním charakteristickým kořenem Proto vyšetříme jeho znaménko a velikost v závislosti na parametrech a

a právě tehdy, když tj. Je-li pak nelze tuto nerovnost splnit; je-li pak je tato nerovnost ekvivalentní s nerovností tj.

Analogicky jako v předchozím případě zjistíme, že právě tehdy, když a

takže neplatí

Celkem dostáváme, že právě tehdy, když a Ještě poznamenejme, že charakteristické kořeny mají stejné znaménko, pokud a mají různá znaménka, pokud

Pokud pak neboť charakteristické kořeny jsou různé. Tato situace nastává právě tehdy, když pro charakteristický kořen platí Řešení úlohy Lineární rovnice (39), Lineární rovnice (40) je v tomto případě tvaru

a řešení úlohy Lineární rovnice (39), Lineární rovnice (40) je součinem geometrické posloupnosti s kvocientem a posloupnosti ohraničené, v níž se pravidelně střídají hodnoty a

• (ii)

Vzhledem k podmínce Lineární rovnice (20) v tomto případě musí být Charakteristická rovnice Lineární rovnice (41) má dvojnásobný kořen a diferenční rovnice Lineární rovnice (39) má řešení

(43)

neboť

Konstanty a volíme tak, aby byly splňeny počáteční podmínky Lineární rovnice (40), tedy jako řešení soustavy lineárních (algebraických) rovnic

Determinant této soustavy je

což znamená, že soustava je jednoznačně řešitelná a že posloupnosti definované vztahy

tvoří fundamentální systém řešení lineární homogenní diferenční rovnice Lineární rovnice (39).

Posloupnost definovaná vztahem Lineární rovnice (43), kde konstanty jsou dány vztahy

je řešením počáteční úlohy Lineární rovnice (39), Lineární rovnice (40). Explicitněji můžeme řešení úlohy Lineární rovnice (39), Lineární rovnice (40) v tomto případě vyjádřit formulí

Řešení diferenční rovnice je v tomto případě součinem geometrické posloupnosti s kvocientem a aritmetické posloupnosti s diferencí

• (iii)

V tomto případě je  Charakteristická rovnice Lineární rovnice (41) má v tomto případě komplexně sdružené kořeny

kde Je tedy

Nyní můžeme vyjádřit řešení diferenční rovnice Lineární rovnice (39) jako posloupnost

(44)

neboť

Konstanty a volíme tak, aby byly splňeny počáteční podmínky Lineární rovnice (40), tedy jako řešení soustavy lineárních (algebraických) rovnic

Determinant této soustavy je

což znamená, že soustava je jednoznačně řešitelná a že posloupnosti definované vztahy

tvoří fundamentální systém řešení lineární homogenní diferenční rovnice Lineární rovnice (39).

Posloupnost definovaná formulí Lineární rovnice (44), kde konstanty jsou dány vztahy

je řešením počáteční úlohy Lineární rovnice (39), Lineární rovnice (40). Explicitněji můžeme řešení úlohy Lineární rovnice (39), Lineární rovnice (40) v tomto případě vyjádřit formulí

Řešení diferenční rovnice je tedy součinem geometrické posloupnosti s kvocientem a posloupnosti ohraničené.

Odtud plyne, že pro je

Poněvadž podle předpokladu je alespoň jedna z počátečních hodnot nenulová, tak pro je

Pro  platí

Výsledky analýzy charakteristické rovnice Lineární rovnice (39) lineární homogenní diferenční rovnice druhého řádu Lineární rovnice (39) jsou zobrazeny na obrázku Lineární rovnice 2.

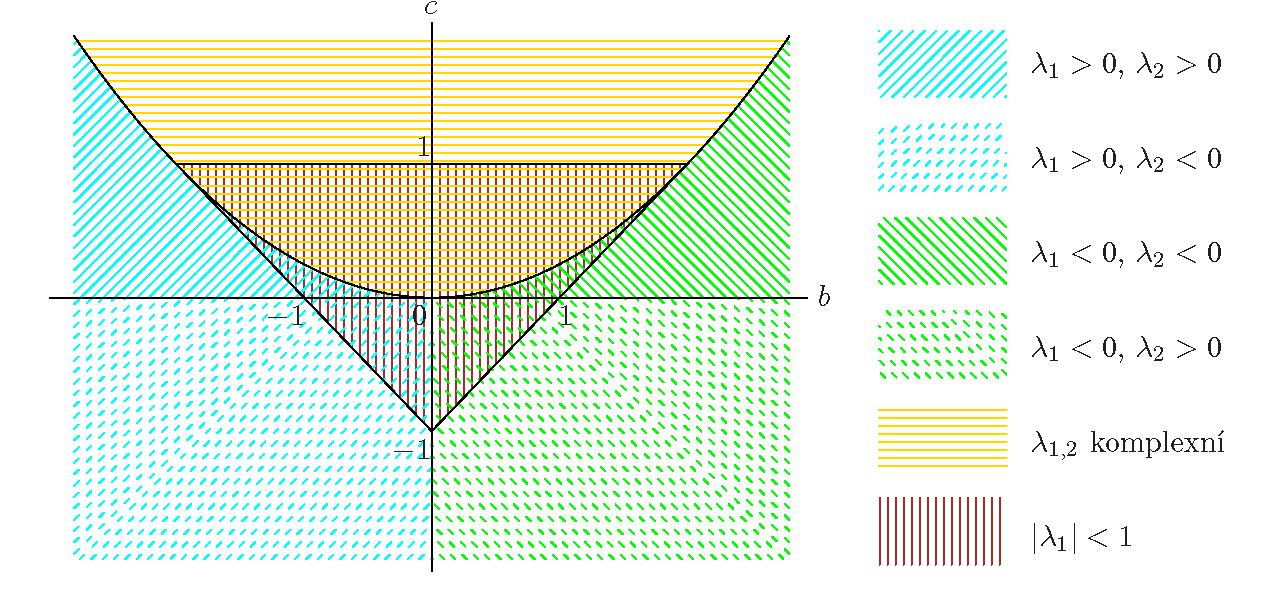Obr. 2. Závislost charakteristických kořenů lineární diferenční rovnice druhého řádu s konstantními koeficienty x(t+2)+bx(t+1)+cx(t)=0 na koeficientech b, c.

Ještě poznamenejme, že pokud by rovnice Lineární rovnice (39) by se redukovala na lineární diferenční rovnici prvního řádu, která má řešení

Úloha Lineární rovnice (39), Lineární rovnice (40) by pak měla řešení jedině v případě