Příklad

Uvažujme jednoduchý Leslieho model populace strukturované do tří věkových tříd, kde jsou plodní jedinci druhé a třetí věkové třídy. Jedná se tedy o model Prolog (14) s Položme konkrétně Budeme předpokládat, že na počátku se populace skládala pouze z jednotkového množství jedinců třetí věkové třídy. Jedná se tedy o model

(15)

Snadno spočítáme, že

a tak můžeme pokračovat dále. Tento výsledek nám ovšem neposkytuje žádnou souhrnnou informaci, která by umožnila nějaký vhled do vývoje populace. A to ani v případě, že ho zobrazíme graficky, viz obr. Prolog 1.

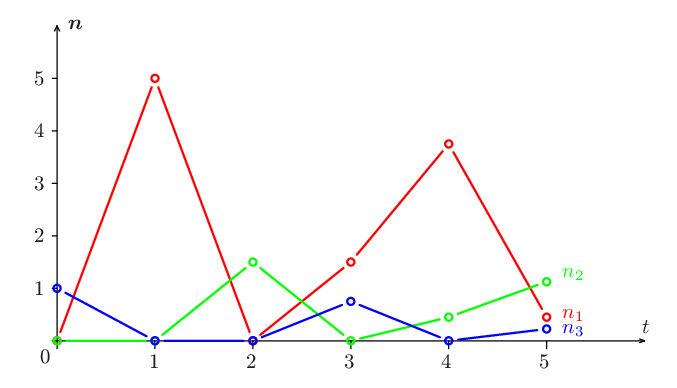Obr. 1. Vývoj populace podle modelu Prolog (15).

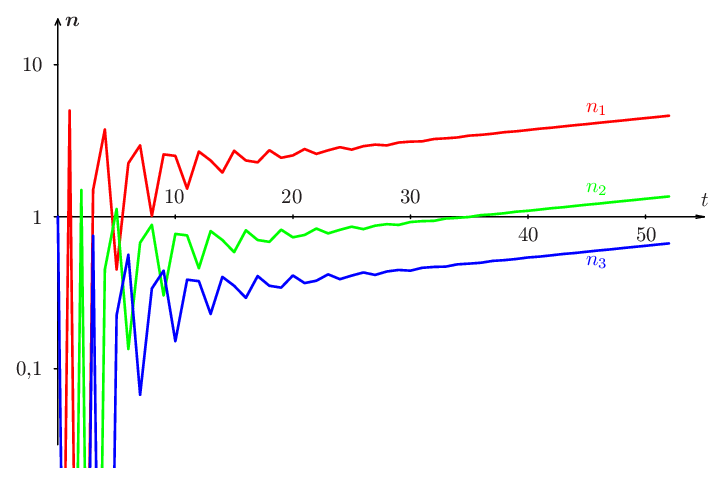Obr. 2. Vývoj populace podle modelu Prolog (15). Na svislé ose je logaritmická stupnice.

Obr. 3. Vývoj věkové struktury populace podle modelu Prolog (15), N=n1+n2+n3.

Vypočítáme proto vývoj populace podle modelu Prolog (15) na delším časovém úseku. Výsledek je prezentován graficky na obr. Prolog 2, na svislé ose (velikosti složek populace) je logaritmická stupnice. Vidíme, že kolísání velikostí jednotlivých věkových tříd se po jisté době (asi po 30 časových jednotkách) ustálí a velikost populace roste exponenciálně, velikosti jednotlivých věkových tříd rostou stejně rychle. To znamená, že po jisté době vývoje se věková struktura populace stabilizuje, relativní zastoupení jednotlivých věkových tříd zůstává konstantní. Tuto úvahu potvrzuje i grafické znázornění vývoje relativních velikostí jednotlivých věkových tříd na obr. Prolog 3. Ještě poznamenejme, že velikost populace modelovaná rovnostmi Prolog (15) s časem roste. Zastoupení jednotlivých věkových tříd ve věkově stabilizované populaci (tj. v populaci po dostatečně dlouhém vývoji) je takové, že relativní abundance třídy s nejmladšími jedinci je největší, relativní abundance třídy s nejstaršími jedinci je nejmenší.