Růstový koeficient populace

Najdeme vlastní hodnoty matice Označme

Determinant rozvineme podle posledního sloupce,

(33)

Odtud je vidět, že pro je

pokud předpokádáme a tedy matice v souladu s Perronovou-Frobeniovou větou nemá nulové vlastní hodnoty.

Rovnost Modely s konstantní projekční maticí (33) lze považovat za lineární diferenční rovnici (rekurentní formuli) prvního řádu pro neznámou posloupnost Jejím řešením je

Poněvadž dostaneme

Vlastní hodnoty matice tedy jsou řešením rovnice

(34)

Levou stranu této rovnice můžeme považovat za funkci proměnné

Při tomto označení je podle Modely s konstantní projekční maticí (31). Dále a

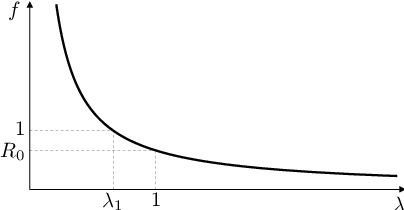
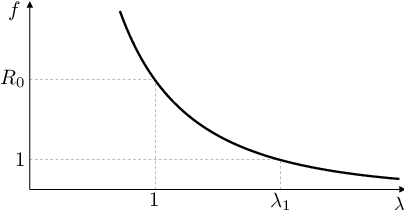
pro To znamená, že na intervalu funkce klesá od nekonečna k nule, takže rovnice Modely s konstantní projekční maticí (34) má jediné kladné řešení, označme ho Hodnota je dominantní vlastní hodnotou matice , tedy Malthusovským koeficientem růstu populace. Pokud pak pokud pak Situace je znázorněna na obrázku Modely s konstantní projekční maticí 1.

Obr. 1. Grafické řešení rovnice Modely s konstantní projekční maticí (34) - charakteristické rovnice Leslieho matice. Vlevo: čistá míra reprodukce R0<1 (vymírající populace), vpravo: R0>1 (rostoucí populace).

Můžeme tedy formulovat závěr:

Je-li pak populace roste, je-li pak populace vymírá. Pokud a populace je strukturně stabilizovaná, pak se její velikost nemění.

Tento výsledek, k němuž jsme dospěli s využitím Perronovy-Frobeniovy teorie, je stejný, jako závěr pravděpodobnostní úvahy provedené v oddíle Čistá míra reprodukce.

Délka generace je definována jako doba, po jejímž uplynutí jsou rodiče vystřídáni potomky stejně starými, jako byli rodiče při jejich narození. Tedy poměr velikosti generace potomků a generace rodičů je roven Tento poměr je však u strukturně stabilizované populace s růstovým koeficientem roven hodnotě Z rovnosti pro délku generace dostaneme vyjádření