Asymptotické vlastnosti

Označme řešení projekční rovnice Modely s interní variabilitou (6) s počáteční podmínkou

Definice 3.1.

• Nechť Množina

se nazývá -limitní množina bodu vzhledem k rovnici Modely s interní variabilitou (6).

• Nechť Množina

se nazývá -limitní množina množiny vzhledem k rovnici Modely s interní variabilitou (6).

• Nechť je taková množina, že

Pak se nazývá invariantní množina rovnice Modely s interní variabilitou (6).

• Nechť je taková invariantní množina rovnice Modely s interní variabilitou (6), že

tj. neexistuje její neprázdná vlastní podmnožina, která by byla invariantní množinou rovnice Modely s interní variabilitou (6). Pak se množina nazývá minimální invariantní množina rovnice Modely s interní variabilitou (6).

Poznámka 3.2. Množina je minimální invariantní množinou rovnice Modely s interní variabilitou (6) právě tehdy, když

Příklad 3.3. Uvažujme rovnici

(8)

která je modelem populace strukturované podle plodnosti Prolog (9), v němž plodnost závisí na velikosti populace. Jedná se tedy o možnou stabilizaci velikosti takové populace omezením plodnosti při vysoké populační hustotě. O parametrech budeme předpokládat, že (juvenilní jedinci mohou přežít a dospět), (plodní jedinci nejsou nesmrtelní) a (plodní jedinci nějaké potomky „produkují“). Z těchto předpokladů bezprostředně plyne, že pokud má počáteční podmínka obě složky nezáporné, pak také řešení rovnice Modely s interní variabilitou (8) má obě složky nezáporné pro všechna Uzavřený první kvadrant je tedy invariantní množinou rovnice Modely s interní variabilitou (8).

Přímým výpočtem se snadno přesvědčíme, že při počáteční hodnotě

je pro všechna Je-li

pak jsou obě složky vektoru kladné. V takovém případě je tedy množina invariantní množinou rovnice Modely s interní variabilitou (8). Odtud dále plyne, že množina v takovém případě není minimální invariantní množinou, neboť má vlastní podmnožinu která je invariantní. Jednoprvková množina již minimální invariantní množinou rovnice Modely s interní variabilitou (8) je.

Definice 3.4. (Typy invariantních množin)  Minimální invariantní množina rovnice Modely s interní variabilitou (6) se nazývá

• stacionární bod (rovnovážný bod, equilibrium), pokud množina je jednoprvková;
   
• cyklus délky (periody) pokud je celé číslo větší než 1 a množina má prvků;
   
• invariantní smyčka, pokud množina je uzavřenou křivkou v prostoru
   
• podivná, pokud není žádného z předchozích typů.

Vektor je stacionární bod rovnice Modely s interní variabilitou (6) právě tehdy, když pro každý čas je tj. vektor je řešením rovnice

(9)

Odtud je vidět, že nulový vektor je stacionárním bodem rovnice Modely s interní variabilitou (6). Tento stacionární bod nazýváme triviální.

Netriviální stacionární body vyjadřují stálou velikost i složení populace - velikosti jednotlivých tříd se v průběhu času nemění; populace je v dynamické rovnováze se svým prostředím.

Cyklus délky je množina taková, že

Zejména pro platí a stacionární bod je tedy nenulovým řešením rovnice

Analogicky lze hledat cykly délky větší než 2.

Definice 3.5. (Stabilita stacionárních bodů). Stacionární bod rovnice Modely s interní variabilitou (6) se nazývá

• stabilní, pokud
   

• asymptoticky stabilní, pokud
   

• globálně asymptoticky stabilní, pokud
   

• repulsivní, pokud

Poznamenejme, že v definici asymptotické stability stacionárního bodu nepožadujeme stabilitu (na rozdíl od Persidského definice asymptotické stability v teorii obyčejných diferenciálních rovnic).

Nechť je stacionární bod rovnice Modely s interní variabilitou (6) a je její řešení. Označme odchylku řešení od stacionárního bodu. Pak a

(10)

Předpokládejme dále, že odchylka od stacionárního bodu je „malá“ (tj. norma vektoru je „malá“) a že složky matice jsou dvakrát spojitě diferencovatelné. Položme

(11)

Z rovnosti Modely s interní variabilitou (10) s využitím Taylorovy věty a rovnosti Modely s interní variabilitou (9) nyní dostaneme

pro libovolné Odtud

To znamená, že odchylka od stacionárního bodu se přibližně vyvíjí jako řešení lineárního homogenního systému diferenčních rovnic s maticí (která nemusí být nezáporná), tj.

kde je řešení úlohy

pokud je „malá“. Označme

(12)

Je-li pak tedy zůstává „malý“ a „malá“ je i odchylka od stacionárního stavu; v důsledku toho je což pro řešení rovnice Modely s interní variabilitou (6) s počáteční podmínkou blízko stacionárního bodu znamená, že

Je-li pak

Provedené úvahy můžeme zformulovat jako větu.

Věta 3.6. Nechť je stacionární bod rovnice Modely s interní variabilitou (6) a matice je v okolí bodu dvakrát spojitě diferencovatelná. Definujme matici rovností Modely s interní variabilitou (11) a číslo rovností Modely s interní variabilitou (12). Pak platí: je-li pak je stacionární bod asymptoticky stabilní, je-li pak je stacionární bod repulsivní.

V případě, že projekční matice závisí na váženém součtu složek vektoru jsou její první parciální derivace ve stacionárním bodě rovny

kde To znamená, že matici můžeme zapsat ve tvaru

Příklad 3.7. Uvažujme opět rovnici Modely s interní variabilitou (8). Podle výsledků uvedených v předchozím příkladu má tato rovnice stacionární bod

Vyšetříme jeho stabilitu.

Označme Pak rovnici Modely s interní variabilitou (8) můžeme psát ve tvaru

Dále je a projekční matice je tedy tvaru

Platí takže

Nyní můžeme vypočítat

Pro zjednodušení zápisu označíme a dostaneme vyjádření matice

přitom

Podle věty Modely s interní variabilitou 3.6 k asymptotické stabilitě stacionárního bodu rovnice Modely s interní variabilitou (8) stačí, aby všechny vlastní hodnoty matice měly modul menší než 1. Z toho můžeme usoudit¹, že kritické hodnoty parametrů jsou takové, kdy má matice vlastní hodnoty rovny 1 nebo -1.

Charakteristická rovnice matice je

kde

Pokud pak tj.

Odtud vyjádříme

a po dosazení za dostaneme takže kritické hodnoty parametrů jsou ty, které vyhovují rovnosti

Pokud pak tj.

Odtud vyjádříme

a po dosazení za

Dostáváme tak druhou množinu kritických hodnot parametrů - ty, které vyhovují rovnosti

Jestliže tedy parametry rovnice Modely s interní variabilitou (8) splňují nerovnosti

pak je stacionární bod rovnice Modely s interní variabilitou (8) asymptoticky stabilní. Ještě si můžeme povšimnout, že na levé straně předchozích nerovností je stejný výraz jako na pravé straně nerovnosti Modely s interní variabilitou (1); můžeme ho tedy interpretovat analogicky.

Obr. 4. Rovnovážný bod v rovnici Prolog (9) s interní variabilitou Modely s interní variabilitou (2)-Modely s interní variabilitou (5). Použité parametry:

Definice 3.8. (Klasifikace minimálních invariantních množin). Minimální invariantní množina rovnice Modely s interní variabilitou (6) se nazývá

• stabilní, pokud ke každému okolí množiny existuje okolí množiny takové, že z plyne pro všechna
   

• atraktor, pokud existuje okolí množiny takové, že z plyne

okolí se nazývá oblast přitažení atraktoru;

• globální atraktor, pokud množina je atraktor a celá množina je jeho oblastí přitažení;
   

• repelor pokud existuje okolí množiny takové, že ke každému počátečnímu stavu existuje čas takový, že

   

   

Obr. 5. Cyklus periody 4 v rovnici Prolog (9) s interní variabilitou Modely s interní variabilitou (2)-Modely s interní variabilitou (5). Použité parametry:

Představu o atraktorech můžeme získat počítačovým experimentem:

1. Zvolíme nějakou „dostatečně reprezentativní“ konečnou podmnožinu oblasti přitažení hledaného atraktoru (například ekvidistantní síť), zvolíme „dostatečně velký“ čas a „dostatečnou dobu“ projekce (mělo by platit ).

2. Vezmeme nějaký bod z množiny

3. Spočítáme řešení příslušné projekční rovnice až do zvolené hodnoty času Tak získáme množinu

4. Kroky 2. a 3. provedeme pro všechny hodnoty

5. Numerickým odhadem atraktoru je množina

V případě, že je dimenze projekční rovnice Modely s interní variabilitou (6) rovna dvěma, nebo maximálně třem, můžeme numericky odhadnutý atraktor znázornit geometricky.

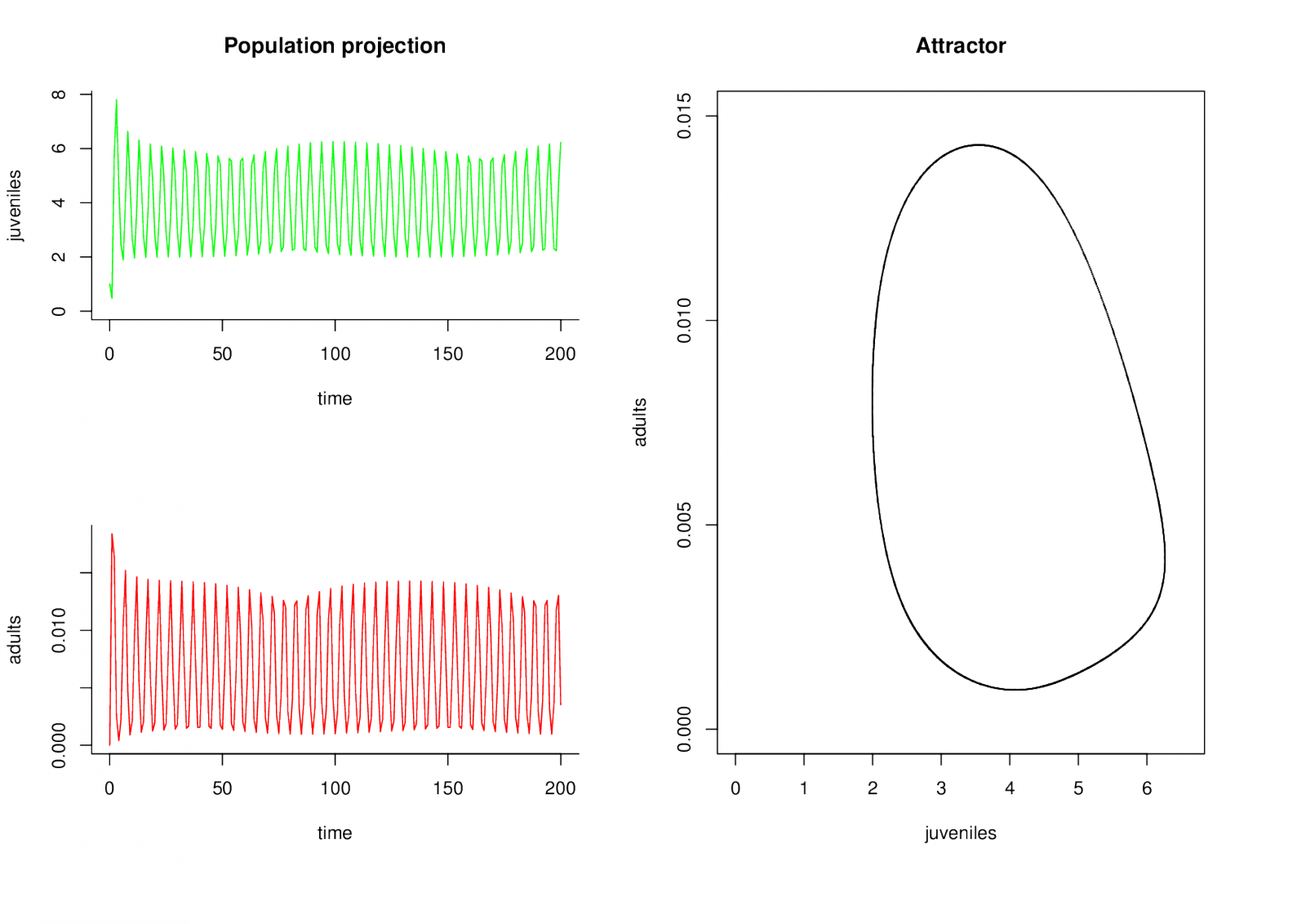
Obr. 6. Invariantní smyčka v rovnici Prolog (9) s interní variabilitou Modely s interní variabilitou (2)-Modely s interní variabilitou (5). Použité parametry:

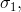
Příklad 3.9.  Podívejme se opět dvojrozměrný model Prolog (9) populace strukturované podle plodnosti. Koeficienty přežívání budou konstantní, koeficienty dospívání a plodnosti a mohou záviset na velikosti jednotlivých tříd podle rovností Modely s interní variabilitou (4) a Modely s interní variabilitou (5).

V tomto modelu se mohou objevit atraktory, které jsou invariantními množinami všech typů zavedených v definici Modely s interní variabilitou 3.4. Příklady možné volby parametrů pro jednotlivé typy jsou uvedeny v popiscích obrázků Modely s interní variabilitou 4 - Modely s interní variabilitou 7. V případě rovnovážného bodu, cyklu délky 4 a podivného atraktoru se jednalo o stabilizaci populace omezením plodnosti, v případě invariantní smyčky o stabilizaci populace odložením reprodukce při vyšších populačních hustotách.

Z obrázků můžeme vypozorovat: Má-li rovnice atraktor rovnovážný bod, pak všechny složky jejího řešení jsou konvergentními posloupnostmi. Má-li rovnice atraktor cyklus, pak složky řešení projekční rovnice po dostatečně dlouhém čase vypadají jako periodické posloupnosti s periodou délky cyklu. Je-li atraktorem invariantní smyčka, na řešení projekčních rovnic můžeme vidět něco jako amplitudovou modulaci základní frekvence. V případě podivného atraktoru není na řešení projekční rovnice kromě ohraničenosti shora i zdola vidět žádná pravidelnost.

Detail atraktoru:

Obr. 7. Podivný atraktor v rovnici Prolog (9) s interní variabilitou Modely s interní variabilitou (2)-Modely s interní variabilitou (5). Použité parametry:

¹Tato úvaha je správná jen tehdy, je-li zaručeno, že matice má pouze reálné vlastní hodnoty.