Příklad - populace strukturovaná podle plodnosti

Uvažujme opět model Prolog (9) popisující vývoj populace, v níž lze jedince rozlišit na juvenilní a dospělé (plodné). Projekční matice populace je tvaru

kde

Charakteristicky polynom matice je na levé straně rovnost Modely s konstantní projekční maticí (4), takže dominantní vlastní hodnota (závisející na všech parametrech) je podle Modely s konstantní projekční maticí (6) rovna

Odtud je vidět, že právě tehdy, když

Zejména

(1)

a právě tehdy, když Jinak řečeno, populace s bezprostředním dospíváním nevymírá právě tehdy, když plodnost násobená pravděpodobností přežití juvenilních jedinců není menší než úmrtnost dospělých.

Každý z ekologických (demografických) parametrů modelu může záviset na velikosti populace nebo na jejím složení (relativním nebo absolutním zastoupením jednotlivých tříd). Velká populace, tj. velká vnitrodruhová konkurence, může omezovat přežití, rychlost dospívání i plodnost:

			(2)
			(3)
			(4)
			(5)

Parametry lze interpretovat jako pravděpodobnosti přežití juvenilních jedinců, přežití plodných jedinců, maturace během projekčního intervalu a specifickou plodnost dospělých jedinců (v tomto pořadí) za předpokladu, že se neprojevuje vnitrodruhová konkurence. Parametry udávají „velikost vlivu“ vnitrodruhové konkurence na přežití, dobu dospívání a plodnost. Všechny parametry jsou nezáporné; pro pravděpodobnosti platí: tj. juvenilní jedinec dospěje v konečném čase, tj. v reálné populaci nemohou všichni jedinci zemřít před dosažením plodnosti, tj. dospělí jedinci nemohou neumírat.

Parametry a budeme chápat jako funkce vektoru Označme

pokud poslední limita existuje. Platí: Je-li pak

tj. populace dlouhodobě přežívá a její velikost je omezená.

Jsou-li funkce a dány rovnostmi Modely s interní variabilitou (2)-Modely s interní variabilitou (5), pak

	pokud
	pokud
	pokud
	pokud

dále

a funkce je spojitou funkcí svých proměnných. Odtud plyne:

• pokud plodnost závisí na velikosti populace podle vztahu Modely s interní variabilitou (5) s a ostatní parametry modelu jsou konstantní, pak velikost populace nemůže růst neomezeně (neboť ) - stabilizace populace zmenšením plodnosti při velké populační hustotě;
   
• pokud převrácená hodnota doby dospívání závisí na velikosti populace podle vztahu Modely s interní variabilitou (4) s a ostatní parametry jsou konstantní, přičemž přežívání juvenilních jedinců není jisté (), pak populace nemůže růst neomezeně - stabilizace populace odložením reprodukce při velké populační hustotě (pojem „odložení reprodukce“ zní jako aktivní schopnost jedince se tak rozhodnout, u mimolidských populací se však většinou jedná o zpomalení růstu a dospívání jedinců, tj. o pasivní odezvu na prostředí);
• pokud pravděpodobnost přežití juvenilních jedinců závisí na velikosti populace podle vztahu Modely s interní variabilitou (2) s a ostatní parametry jsou konstantní, pak populace nemůže růst neomezeně - stabilizace populace zvětšením úmrtnosti juvenilních jedinců (nebo infanticidou) při velké populační hustotě;
   
• i když pravděpodobnost přežití dospělých jedinců závisí na velikosti populace podle vztahu Modely s interní variabilitou (3) s může populace růst neomezeně; k tomu například dojde, když plodnost je velká,

Stejné úvahy se stejnými závěry lze provést i v případě, že parametry a závisí na velikosti populace jiným způsobem, než podle vztahů Modely s interní variabilitou (2)-Modely s interní variabilitou (5), ale stále mají vlastnost

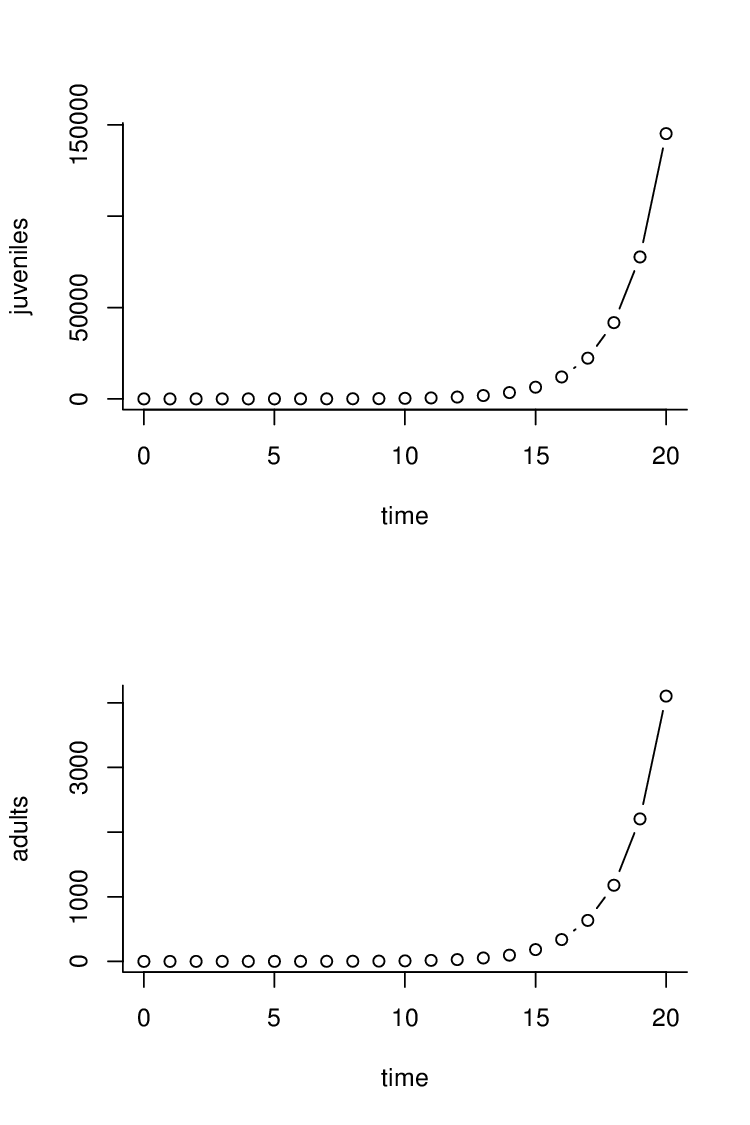
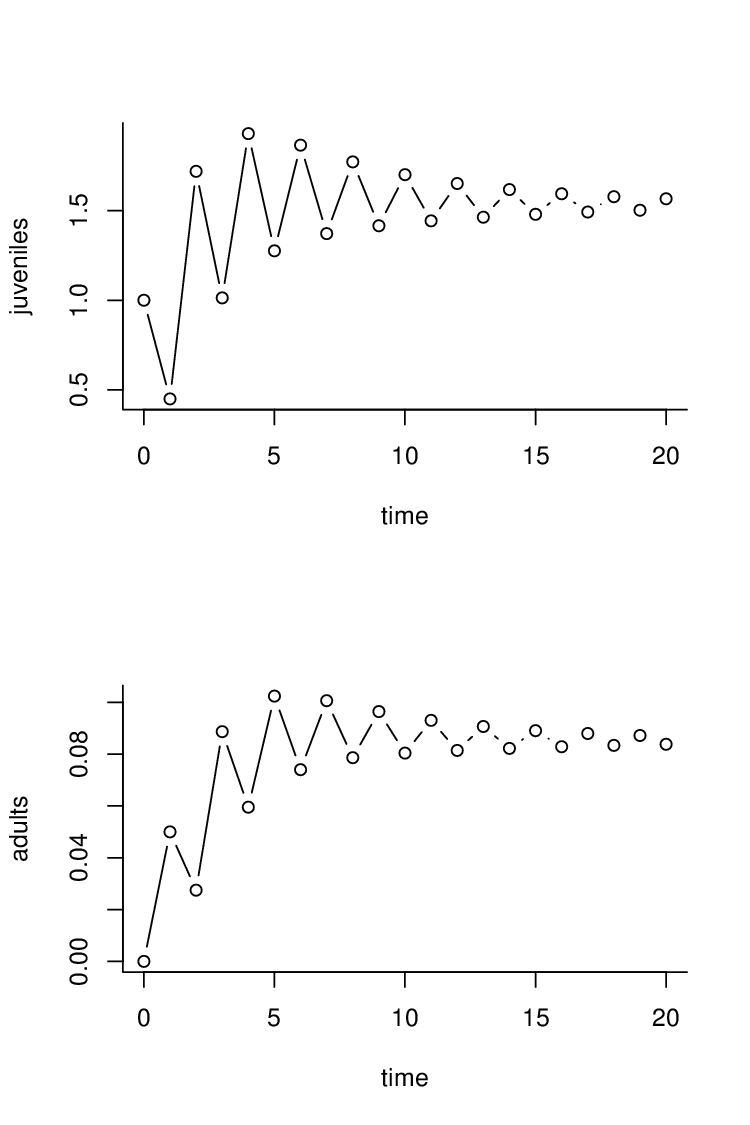
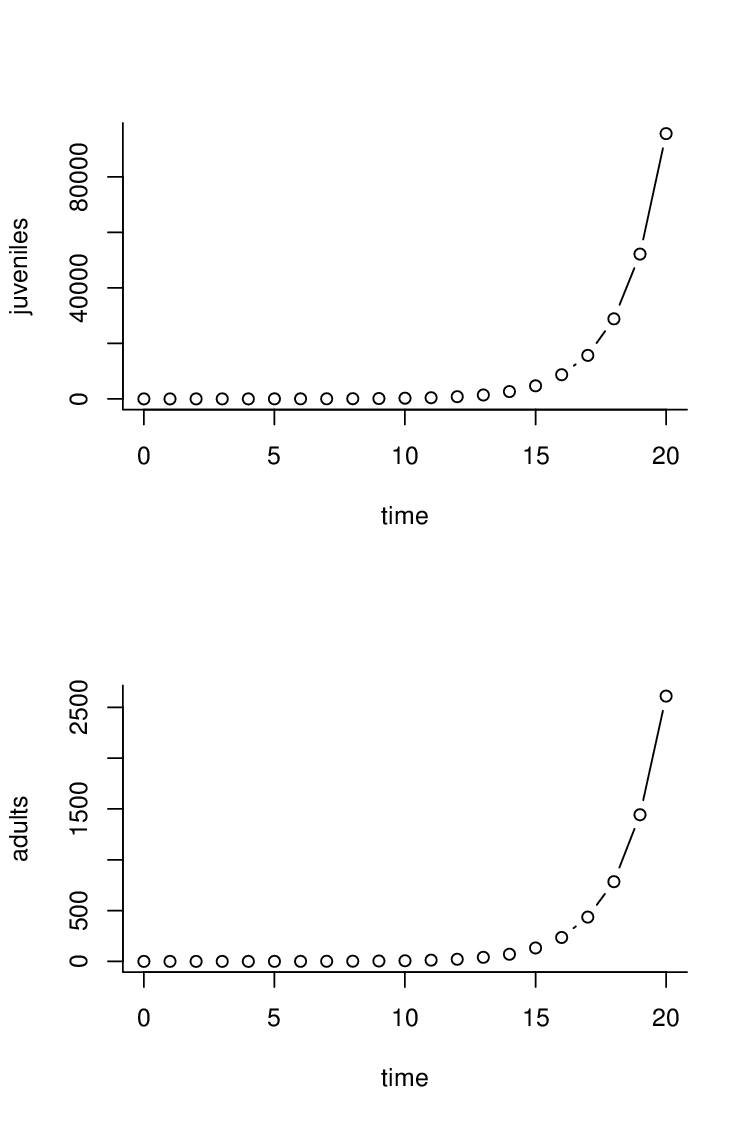
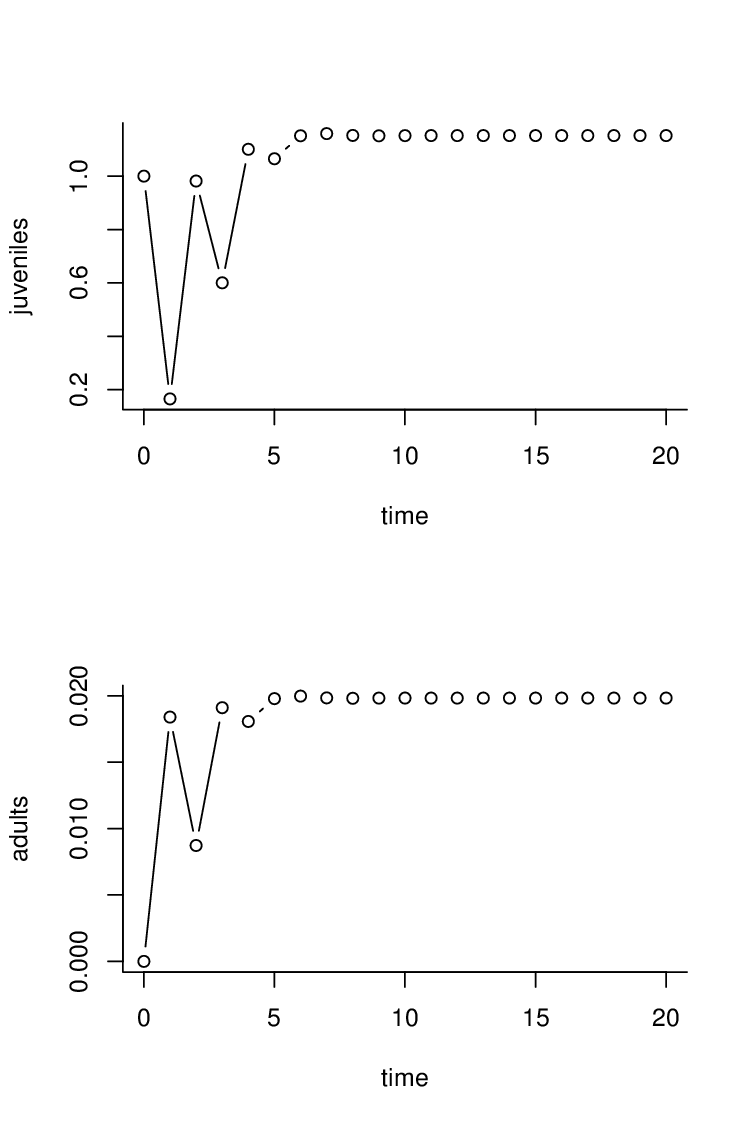
Na obrázku Modely s interní variabilitou 1 vlevo je znázorněna dynamika populace, jejíž ekologické (demografické) charakteristiky nezávisejí na populační hustotě. Na obrázcích Modely s interní variabilitou 1 vpravo, Modely s interní variabilitou 2, Modely s interní variabilitou 3 vlevo jsou příklady populace se stejnými hodnotami parametrů a takových, že právě jeden z ekologických (demografických) parametrů závisí na velikosti (hustotě) populace. U populace na obr. Modely s interní variabilitou 3 vlevo se projevuje vliv vnitrodruhové konkurence na přežití dospělých jedinců (např. vnitrodruhová agresivita rostoucí s populační hustotou); tento vliv však nezajistí regulaci velikosti populace. Vliv vnitrodruhové konkurence na přežití dospělých stabilizuje velikost populace při nižší plodnosti, obr. Modely s interní variabilitou 3 vpravo.

Obr. 1. Vývoj populace strukturované podle plodnosti. Použité parametry: Vlevo: Ekologické parametry nezávisí na velikosti populace, tj. a v důsledku Vpravo: Plodnost závisí na velikosti populace, ostatní parametry nikoliv, tj. a v důsledku Stabilizace populace omezením plodnosti.

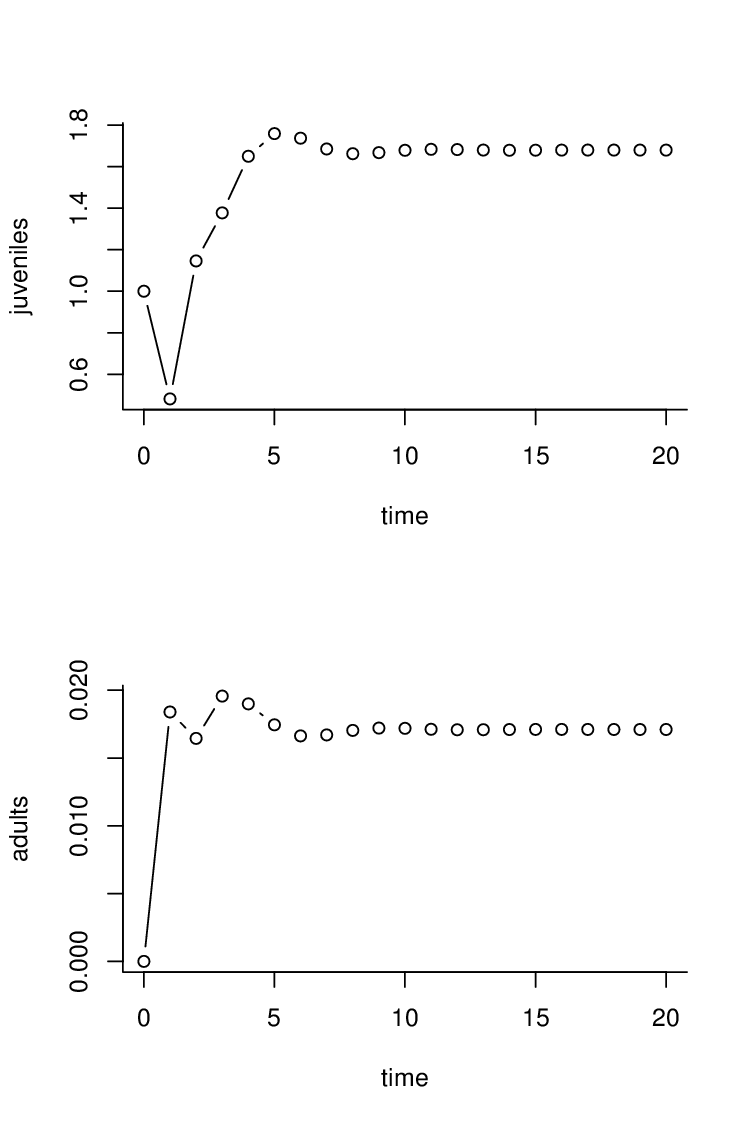
Obr. 2. Vývoj populace strukturované podle plodnosti. Použité parametry: Vlevo: Dospívání závisí na velikosti populace, ostatní parametry nikoliv, tj. a v důsledku Stabilizace populace odložením reprodukce. Vpravo: Přežití juvenilních závisí na velikosti populace, ostatní parametry nikoliv, tj. a v důsledku Stabilizace populace zvětšením úmrtnosti juvenilních (infanticidou).

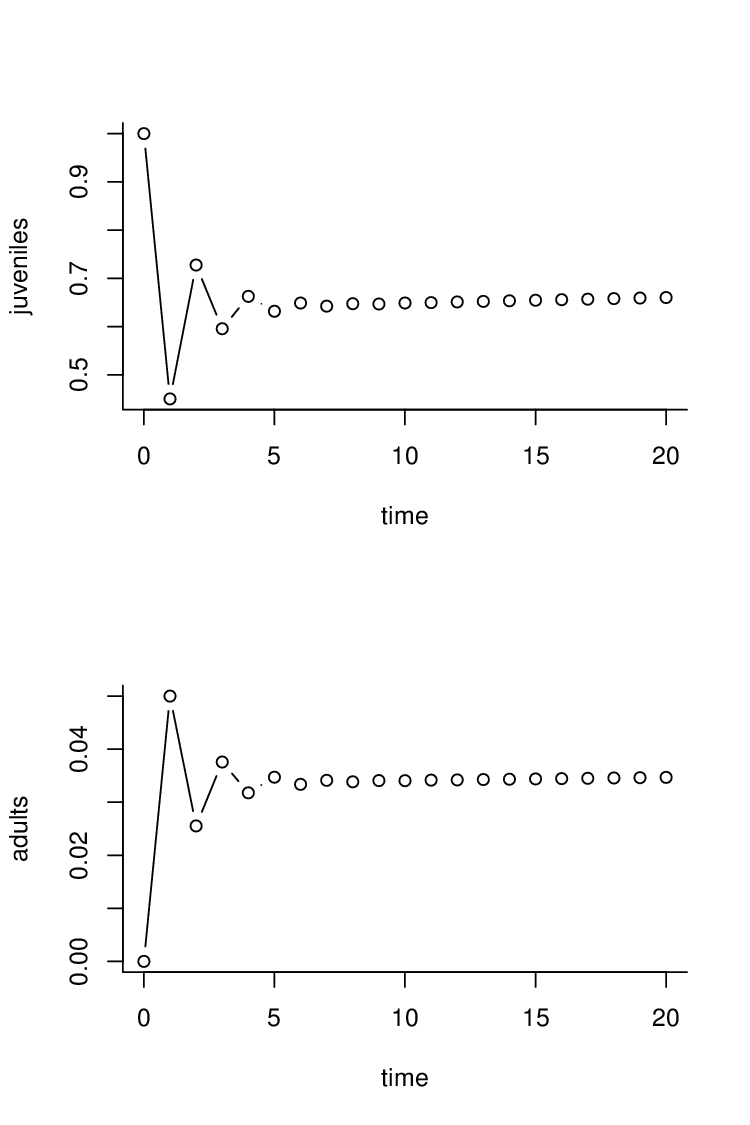
Obr. 3. Vývoj populace strukturované podle plodnosti. Použité parametry: Vlevo: Přežití dospělých závisí na velikosti populace, ostatní parametry nikoliv a fertilita je velká, tj. a v důsledku Zpomalení růstu zvětšením úmrtnosti dospělých. Vpravo: Přežití dospělých závisí na velikosti populace, ostatní parametry nikoliv a fertilita je malá, tj. a v důsledku Stabilizace populace zvětšením úmrtnosti dospělých.