Předpokládejme, že jedinci jsou roztříděni podle plodnosti; v první třídě jsou jedinci juvenilní, ve druhé jsou jedinci plodní. V tomto případě tedy je Předpokládejme, že jedinci ve třídě mladých neplodných buď uhynou nebo přežijí. Pokud přežijí, mohou dospět nebo zůstat neplodnými. Přitom předpokládáme, že dospívání a přežívání jsou stochasticky nezávislé procesy. Ve třídě dospělých jedinci buď přežijí nebo uhynou. Před tím však „vyprodukují“ nějaké potomky. Časová jednotka je tedy volena tak, aby během projekčního intervalu měl jeden plodný jedinec nejvýše jednu „várku“ potomstva (vrh, snůšku a podobně).

Označme resp. podíl juvenilních, resp. plodných, jedinců, kteří přežijí jednotkový časový interval, podíl přežívajících juvenilních jedinců, kteří během tohoto časového intervalu dospějí a počet potomků plodného jedince během jednotkového časového intervalu. Specifický příspěvek první třídy do sebe samé představují juvenilní jedinci, kteří během projekčního intervalu neuhynuli a nedospěli, z předpokládané nezávislosti přežívání a dospívání je tento příspěvek roven Podobně specifický příspěvek první třídy do druhé představují jedinci, kteří projekční interval přežili a během něho dospěli, je tedy roven Příslušný graf životního cyklu tedy je:

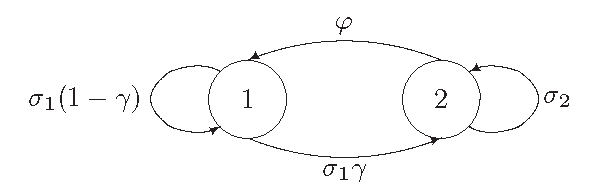
Projekční matice v tomto případě je tvaru

Jedná se tedy o modifikovaný model Fibonacciových králíků Prolog (9).

Příklad 2. Věkově strukturovaná populace

Nejprve zvolíme délku projekčního intervalu, tj. časovou jednotku (pro lidskou populaci je obvyklou jednotkou jeden rok, pro populace velkých savců by vhodnou jednotkou byl rok až desetiletí, pro drobné savce týden až měsíc). Za tuto časovou jednotku jedinec, který přežije, zestárne o stejnou hodnotu. Předpokládejme, že žádný jedinec se nemůže dožít věku vyjádřeného v příslušných jednotkách (volíme ), tj. že nejvyšší možný věk je Jedince rozdělíme do věkových tříd: v -té třídě jsou jedinci věku z intervalu Označme podíl jedinců z -té třídy, kteří jednotkový interval přežijí; ekvivalentně, je (klasická) pravděpodobnost, že jedinec věku přežije jednotkový časový interval.

Dále budeme předpokládat, že jedinci od věku 2 mohou „produkovat“ potomky, tj. že jedinci třídy pro přispívají do třídy 1, třídy novorozenců. Označme počet potomků jedince -té třídy. Příslušný graf životního cyklu je:

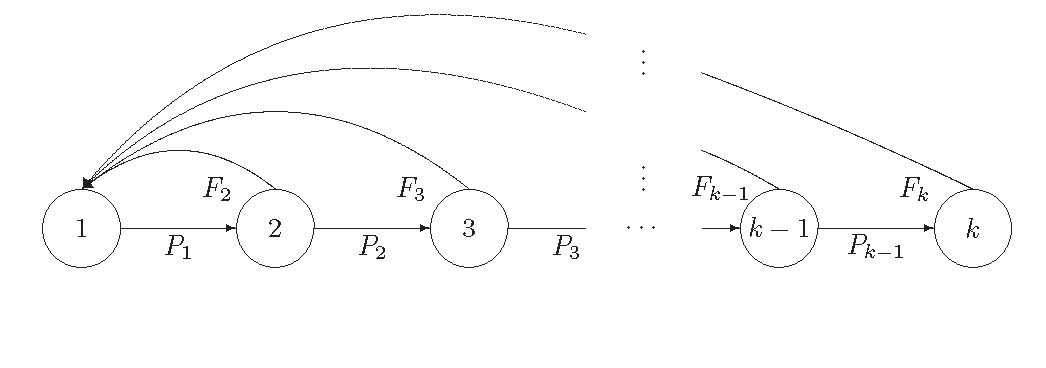
V tomto případě je projekční matice tvaru

To je Leslieho matice s parametrem a model věkově strukturované populace je klasickým Leslieho modelem Prolog (14).

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity