Uvažujme populaci, v níž jsou jedinci dvou pohlaví a jedinci každého pohlaví jsou rozlišeni na juvenilní a plodné. Juvenilní jedinci mohou přežívat a dospívat, plodní jedinci produkují gamety a mohou přežívat. Jedná se tedy o „dvojpohlavní analogii“ populace, jejíž model byl sestaven v Prologu.

Za začátek životního cyklu takové populace budeme považovat spojení samičí a samčí gamety, kterým vznikne zatím bezpohlavní zygota, ze které se vyvine buď mladá samička nebo sameček. Za jednotku času zvolíme dobu, za niž ze zygoty vznikne jedinec. Označme množství životaschopných zygot v čase tj. takových zygot, z nichž vznikne živý jedinec. Dále označme a resp. a množství juvenilních a plodných samic, resp. samců. Analogicky jako v případě nepohlavní populace označíme nebo pravděpodobnosti, že juvenilní samička nebo sameček dospěje během časového intervalu jednotkové délky, a a označíme pravděpodobnosti, že jednotkový čas přežije juvenilní samička, juvenilní sameček, plodná samice a plodný samec (v tomto pořadí). Primární poměr pohlaví, tj. relativní zastoupení zygot, z nichž se vyvinou samičky, označíme Nakonec označíme symbolem počet zygot, které během jednotkového času vyprodukují plodní jedinci. Tento počet bude určitě nějak záviset na aktuálním množství samic a samců aktuálně přítomných v populaci, tedy v uvažovaném modelu je

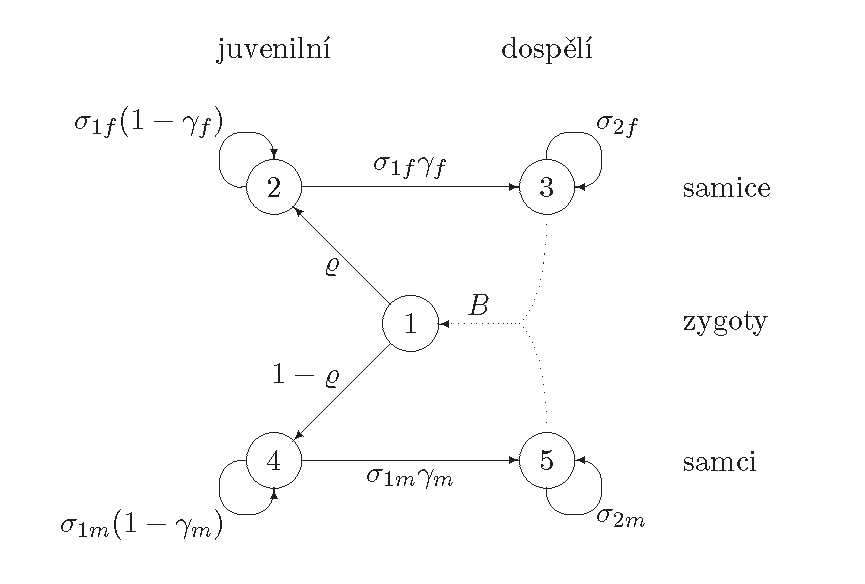
Životní cyklus uvažované populace je znázorněn na obr. Modely dvojpohlavní populace 1.

Obr. 1. Schematické znázornění životního cyklu dvojpohlavní populace strukturované na juvenilní (neplodné) a dospělé (plodné) jedince. Uzel representuje zygoty, které jsou produkovány společně dospělými samicemi a samci ale které ještě nemají určité pohlaví. Parametr označuje primární poměr pohlaví, parametry pravděpodobnost maturace během projekčního intervalu, parametry a pravděpodobnosti přežití juvenilních a dospělých jedinců příslušného pohlaví.

Nejedná se ovšem o graf životního cyklu ve vlastním slova smyslu; do uzlu vede „hrana“ vycházející ze dvou uzlů a

Vývoj modelované populace lze popsat rovnostmi

nebo v maticovém tvaru


	(1)

Opět se nejedná o maticový model v obvyklém smyslu; model je porušen (perturbován) přičítaným vektorem, který závisí na struktuře populace a tato závislost je nelineární.

Funkce vyjadřující množství „vyprodukovaných“ zygot bývá nazývána funkce rození (birth function) nebo funkce manželství (mariage function). Tvar této funkce je potřebné specifikovat.

Funkce rození přiřadí danému množství plodných samic a samců množství jimi vyprodukovaných zygot. Měla by mít následující vlastnosti:

tj. množství vyprodukovaných zygot je nezáporné číslo.
pro jakékoliv tj. pokud v populaci chybí plodné samice nebo samci, nebudou žádné nové zygoty.
pro každé tj. funkce je homogenní prvního řádu. Tato vlastnost vyjadřuje, že počet „vyprodukovaných“ zygot se mění ve stejném poměru, v jakém se změní množství dospělých samic i samců; například, pokud se zdvojnásobí množství plodných samic i samců, pak se zdvojnásobí i počet „vyprodukovaných“ zygot (pro ).
Funkce je neklesající v každém svém argumentu, tj. zvětší-li se množství plodných samic (nebo samců), množství „vyprodukovaných“ zygot se nezmenší.

První dvě vlastnosti jsou přirozené, třetí a čtvrtá mohou být předmětem diskuse. Např. zdvojnásobí-li se počet plodných samic i samců, může být výsledné množství vyprodukovaných zygot větší než dvojnásobné (při větší populační hustotě může být větší šance, že se samice se samcem setkají, projevuje se Alleeho efekt), nebo menší než dvojnásobné (při velké populační hustotě mohou být spotřebovány zdroje prostředí a na jedince zbývá méně energie pro produkci gamet, projevuje se vnitrodruhová konkurence). Podobné námitky lze mít i proti neklesání funkce

Můžeme uvažovat různé strategie oplodňování. Jedna extrémní možnost je tvorba trvalých párů, tj. že jeden samec během jednotkového času oplodní nejvýše jednu samici a jedna samice je oplodněna nejvýše jedním samcem. Navíc těchto párů je maximální možný počet - pokud není samic méně než samců, pak všichni samci realizují své spermie, pokud není samic více než samců, pak všechny samice jsou oplodněné. Druhá krajnost je ta, že všechny dospělé samice jsou oplodněny, pokud je v populaci alespoň jeden plodný samec, nebo že všichni samci realizují své gamety, pokud je v populaci alespoň jedna samice (to je možné například u dvoudomých rostlin). Samozřejmě může nastat také nějaká možnost mezi těmito krajnostmi. Tyto úvahy vedou k závěru, že hodnoty funkce mohou být úměrné některému z následujících výrazů:

Všechny takové funkce splňují vlastnosti (i)-(iv).

Předpokládejme nyní, že známe funkci Pro libovolné hodnoty a položíme

Pak

a model Modely dvojpohlavní populace (1) můžeme přepsat jako maticový model tvaru

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity