Slovník | Vyhledávání | Mapa webu
 
Analýza a modelování dynamických biologických datMaticové populační modely Dodatek: Perronova-Frobeniova teorie 2
plochá struktura
Logo Matematická biologie

Dodatek: Perronova-Frobeniova teorie 2

Tvrzení 1.16. Nechť jsou všechny její různé vlastní hodnoty takové, že Pak a
Důkaz. Označme tj. Nejprve si všimneme několika jednoduchých fakt:
  1.  Z tvrzení Dodatel 1.15 plyne, že k vlastní hodnotě existuje regulární diagonální matice taková, že
     
  2. Matice a mají stejné vlastní hodnoty. Je-li totiž vlastní hodnotou matice pak matice je singulární a tedy také matice je singulární, což znamená, že je také vlastní hodnotou matice Podobně nahlédneme, že libovolná vlastní hodnota matice je také vlastní hodnotou matice .
     
  3. je vlastní hodnotou matice právě tehdy, když je vlastní hodnotou matice neboť matice a jsou současně singulární nebo regulární.
     
  4. Je-li vlastní hodnotou matice pak je také vlastní hodnotou matice neboť matice je reálná. Odtud dále plyne, že pro nějaké tj. neboť jsou všechny vlastní hodnoty stejného modulu.

Je-li je tvrzení triviální. Je-li pak - kdyby totiž měla nenulovou imaginární část, pak by také byla vlastní hodnotou různou od i což by bylo ve sporu s předpokladem, že jsou všechny vlastní hodnoty stejného modulu. To znamená, že

Buď Je-li je vlastní hodnotou matice pak podle iii. je vlastní hodnotou matice takže podle i. je také vlastní hodnotou matice Nyní podle ii. je vlastní hodnotou matice což
znamená, že existuje že

neboť To znamená, že To je však možné jen tak, že a tedy Analogicky lze ukázat, že

Odtud plyne, že vlastní hodnoty jsou vrcholy pravidelného -úhelníku se středem 0 v komplexní rovině, tedy

Buď nyní libovolný index. Z rovnosti

plyne rovnost

Jsou-li tedy lineárně nezávislé vlastní vektory matice příslušné k vlastní hodnotě pak jsou vlastní vektory matice příslušné k vlastní hodnotě které jsou lineárně nezávislé. To znamená, že

Analogicky z toho, že rovnost implikuje rovnost odvodíme nerovnost Celkem tedy dostaneme, že platí rovnost

Tvrzení 1.17. Je-li ireducibilní, pak   příslušný vlastní vektor a

Důkaz. Nejprve ukážeme, že ireducibilní nezáporná matice nemá nulový sloupec: Připusťme, že existuje index takový, že pro všechna Pak pro libovolné je

což je spor s ireducibilitou.

Položme

Pak a

tedy takže Odtud plyne

Poněvadž matice je ireducibilní, ke každé dvojici indexů existuje číslo takové, že Položme Pak

a pro libovolný vlastní vektor matice příslušný k vlastní hodnotě platí

tedy je současně nezáporný vlastní vektor kladné matice příslušný k vlastní hodnotě Podle tvrzení Dodatek 1.5 je a tedy

Z uvedeného výpočtu dále plyne, že

Prostor na pravé straně inkluze je podle tvrzení Dodatek 1.8 jednodimenzionální a tedy

 
Věta 1.18. Buď nezáporná matice. Pak existuje její vlastní hodnota taková, že pro každou vlastní hodnotu matice a existuje nezáporný vlastní vektor příslušný k vlastní hodnotě

Je-li navíc matice primitivní, pak   pro libovolnou vlastní hodnotu matice příslušný vlastní vektor a je jednodimenzionální.

Je-li navíc matice ireducibilní a imprimitivní, pak příslušný vlastní vektor a existují vlastní hodnoty takové, že a je jednodimenzionální,

Důkaz. První část je tvrzení Dodatek 1.13, druhá část je tvrzení Dodatek 1.14, třetí část je tvrzení Dodatek 1.16 a Dodatek 1.17.

Poznámka 1.19. Číslo z třetí části věty Dodatek 1.18 je větší než 1. Tato vlastnost však nebyla dokázána.

Klasifikace nezáporných matic a odpovídající vlastnosti vlastních hodnot a vlastních vektorů jsou shrnuty v obrázku Dodatek 1.
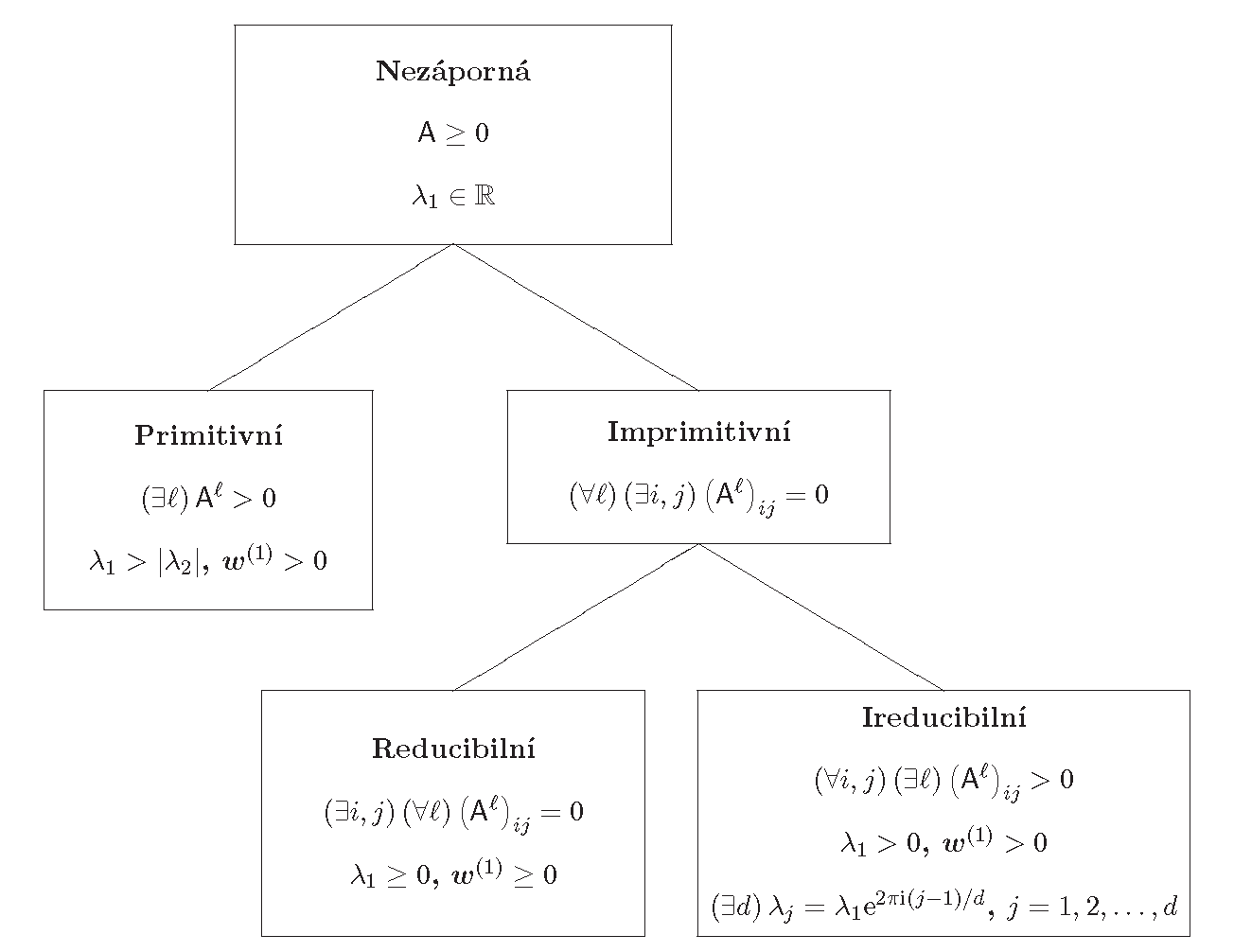Obr. 1. Klasifikace nezáporných matic a charakterizace jejich vlastních hodnot a vlastních vektorů. Vlastí hodnoty matice jsou uspořádané tak, že
označuje vlastní vektor příslušný k vlastní hodnotě
 
vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity