2.3 Několik řešených příkladů
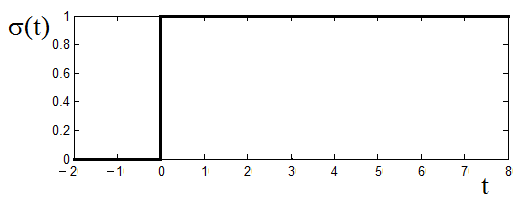
Příklad 2.1. Určeme spektrální funkci jednotkového skoku.
 |
 |
 |
 |
|
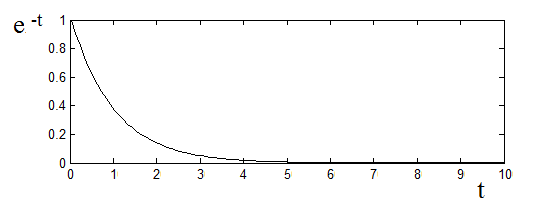
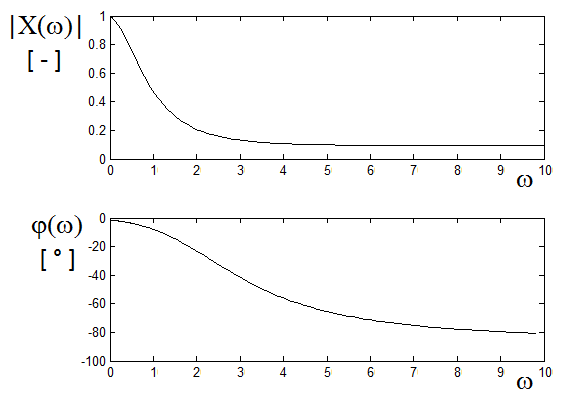
Obr. 7. Časový průběh a spektrální funkce exponenciály e-
|
Obr. 8. Časový průběh a spektrální funkce jednotkového skoku
|
Řešení. Jednotkový skok
bohužel nevyhovuje podmínce absolutní integrovatelnosti, tzn. že neexistuje Fourierův integrál. Pomůžeme si proto pomocí exponenciální funkce (obr. Modely veličin spojitých v čase III 7)
|
|
(26) |
Protože funkce má nenulový průběh pouze pro
lze použít Fourierův integrál pouze v mezích od
do
Je tedy
|
|
(27) |
Za jednotkový skok lze považovat výše uvedenou exponenciální funkci za předpokladu, že útlum
a koeficient
Potom
|
|
(28) |
a tedy (obr. Modely veličin spojitých v čase III 8).
|
|
(29) |
Příklad 2.2. Určete spektrální funkci obdélníkového impulzu o výšce
době trvání
a s náběžnou hranou v počátku časové osy.
 |
|
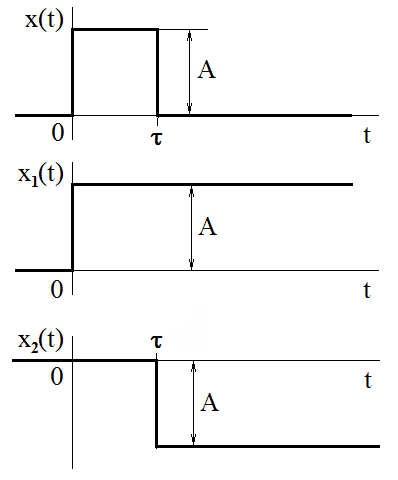
Obr. 9. Konstrukce obdélníkového impulzu ze vzájemně posunutých skokových funkcí
|
Řešení. Obdélníkový impulz o požadovaných vlastnostech můžeme zkonstruovat ze vzájemně posunutých skokových funkcí, jak je znázorněno na obr. Modely veličin spojitých v čase III 9. Spektrum jednotkového skoku jsme spočítali v předchozím příkladu a co se spektrem mimo jiné udělá posunutí v čase řeší kap. 2.2 Vlastnosti Fourierovy transformace. Platí tedy
|
|
(30) |
Potom je
|
|
(31) |
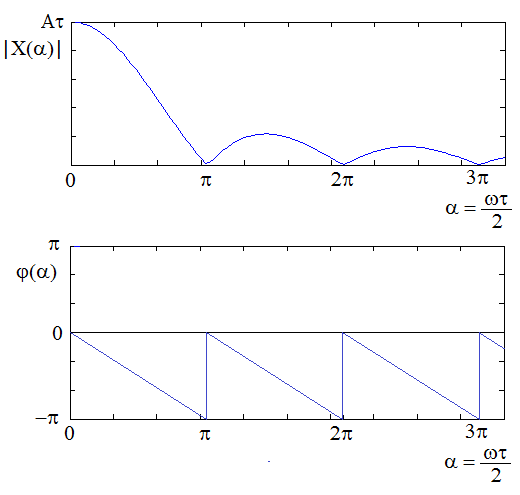
Z toho plyne, že modul spektrální hustoty je dán vztahem
|
|
(32) |
Modul spektrální funkce je dán průběhem funkce
Nulové hodnoty nabývá tato funkce pro hodnoty argumentu rovny celočíselným násobkům
tj. pro
|
|
(33) |
resp.
|
|
(34) |
a tedy
|
|
(35) |
To znamená, že čím je obdélníkový impulz užší, tím plošší je jeho modulová spektrální funkce.
Fázové spektrum je dáno součtem funkce
|
|
(36) |
a fáze vyplývající ze změny znaménka funkce.
Příklad 2.3. Určete spektrum Diracova impulzu.
Řešení. Diracův impulz má z pohledu svého vztahu k funkcím některé poněkud nestandardní vlastnosti. Zkusme proto vyřešit úlohu raději jednoduchou úvahou na základě dříve dosažených výsledků.
 |
 |
|
Obr. 10. Spektrální funkce obdélníkového impulzu - a) modulové spektrum; b) fázové spektrum
|
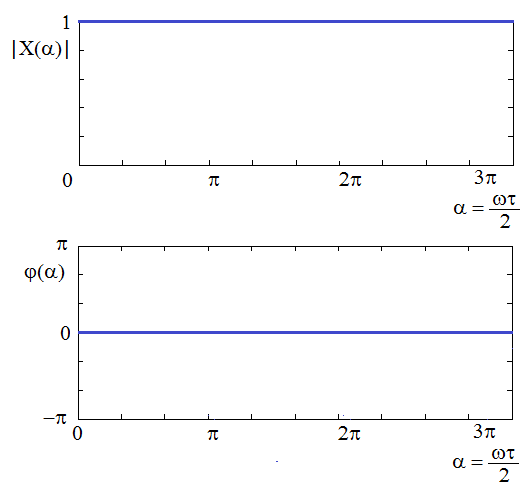
Obr. 11. Spektrální funkce jednotkového impulzu
|
Protože jednotkový impulz můžeme považovat za obdélníkový impulz s limitně nulovou šířkou a limitně nekonečnou výškou, jejichž součin je roven
pak součin
definující multiplikativní koeficient u modulové spektrální funkce obdélníkového impulzu (vztah Modely veličin spojitých v čase III (31)) je roven jedné a první nulové hodnoty dosahuje spektrální funkce pro
To znamená, že modul spektrální funkce jednotkového impulzu je roven 1 pro všechny frekvence a fáze je v celém frekvenčním rozsahu nulová.
Můžeme také s využitím Modely veličin spojitých v čase III (18) a vztahu pro vzorkovací vlastnost jednotkového impulzu (Modely veličin spojitých v čase I (23)) psát, že
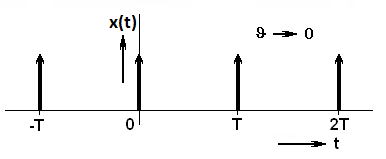
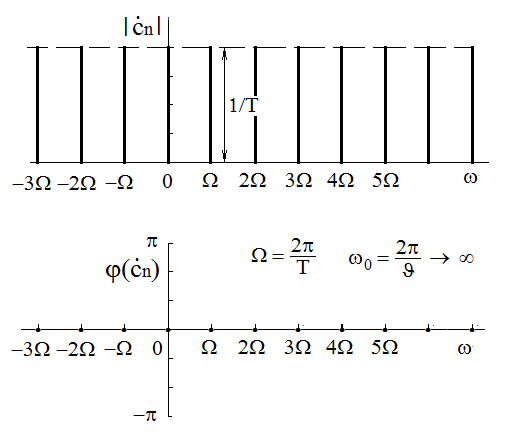
Příklad 2.4.Určete spektrum periodického sledu Diracových impulzů s periodou
Řešení. Podobně jako v případě jednorázového jednotkového impulzu, lze i v tomto případě nalézt řešení rozborem dříve řešeného případu periodického obdélníkového pulzu.
Z periodického charakteru funkce vyplývá, že její spektrum musí být diskrétní. Nabývá hodnot pouze pro frekvence rovné celočíselným násobkům základní úhlové frekvence, která je dána periodou
opakování impulzů, tj.
Protože hodnoty modulů Fourierových koeficientů
obdélníkového pulsu jsou dány hodnotami funkce
(připomeňme obr. Modely veličin spojitých v čase III 4) a protože doba trvání jednotlivých impulzů
jde limitně k nule, posouvá se první nulová hodnota funkce
limitně do nekonečna. Moduly jednotlivých koeficientů proto nabývají konstantních hodnot rovných
a fáze je, vzhledem ke kladným reálným hodnotám koeficientů, rovna nule.
Příklad: 2.5. Předpokládejme, že funkce
má spektrální funkci
a funkce
má spektrální funkci
Určete vztah pro Fourierovu transformaci funkce, která se rovná konvoluci obou dílčích funkcí
a
tj. odvoďte vztah Modely veličin spojitých v čase III (25).
Řešení. Konvoluce
dvou dílčích funkcí
a
je dána podle vztahu
Fourierovu transformaci funkce
spočítáme jako
|
|
(37) |
Vnitřní integrál představuje Fourierovu transformaci funkce
posunutou v čase o
Podle vztahu Modely veličin spojitých v čase III (22) pro spektrum takové funkce platí
Dosadíme-li z tohoto výrazu do Modely veličin spojitých v čase III (37), dostaneme
(38)
Protože
není funkcí
, lze tento člen vytknout před integrál
|
|
(39) |
V tomto případě integrál v druhé části vztahu Modely veličin spojitých v čase III (39) představuje Fourierovu transformaci funkce
resp.
takže můžeme psát, že
|
|
(40) |