
Matematické operace s komplexními čísly
Rovnost dvou komplexních čísel
Dvě komplexní čísla a
v kartézském tvaru jsou si rovna, pokud platí
|
|
(7) |
Dvě komplexní čísla a
v exponenciálním tvaru jsou si rovna, pokud platí
|
|
(8) |
Ekvivalentně platí vztah Komplexní čísla (8) i pro goniometrický tvar komplexních čísel.
Sečítání a rozdíl dvou komplexních čísel
Pro sečítání komplexních čísel a
platí
|
|
(9) |
Pro rozdíl dvou komplexních čísel pak ekvivalentně je
|
|
(10) |
Příklad 2.1. Sečtěte komplexní čísla
a
Řešení.

Součin a podíl dvou komplexních čísel
Součin dvou komplexních čísel a
v kartézském tvaru se určí podle vztahu
|
|
(11) |
Komplexní čísla tedy násobíme jako dvojčleny a využijeme vztah
Součin dvou komplexních čísel
a
v exponenciálním tvaru určíme podle vztahu
Pro sečítání a násobení dvou, případně více komplexních čísel platí následující pravidla:
|
asociativní zákon: |
|
| komutativní zákon: |
|
| distributivní zákon | |
| pro každé |
|
| ke každému x existuje takové číslo |
|
| ke každému |
|
Podíl dvou komplexních čísel a
v kartézském tvaru je dán vztahem
|
|
(12) |
Podíl dvou komplexních čísel a
v exponenciálním tvaru je dán vztahem
|
|
(13) |
Pro operace s komplexně sdruženými čísly platí
|
|
(14) |
Příklad 2.2. Mějme komplexní čísla
a
Určete jejich součet, rozdíl, součin a podíl.
Řešení.
Příklad 2.3. Vynásobte komplexní čísla
a
Řešení.
Uspořádání komplexních čísel
Na rozdíl od reálných čísel nelze komplexní čísla uspořádat, tj. nelze je seřadit podle velikosti tak, aby se toto seřazení rozumně chovalo z hlediska základních matematických operací.
Umocňování a odmocňování komplexních čísel
Věta 2.4. (Moivrova). Pro každé reálné a celočíselné
je
|
|
(15) |
Z Moivrovy věty pak pro celočíselné umocňování komplexních čísel v geometrickém, resp. exponenciálním tvaru různých od nuly je
|
|
(16a) |
resp.
|
|
(16b) |
Pro přirozené číslo k je -tá odmocnina
z komplexního čísla
takové číslo
pro které platí
|
|
(17) |
Je-li od nuly různé, existuje právě k různých hodnot odmocniny
pro které je
|
|
(18) |
pro
Pro je
Příklad 2.5. Určete
pokud je
Řešení. Podle Moivrovy věty je
Příklad 2.6. Určete
Řešení. S aplikací Moivrovy věty a z ní vyplývajícího vztahu Komplexní čísla (18) je
To znamená, že je
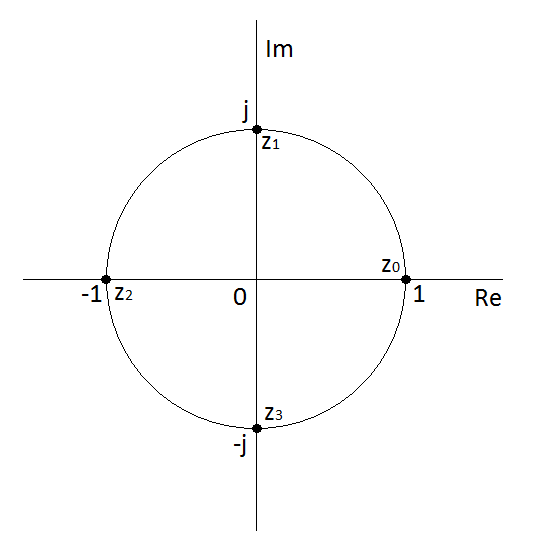
Příklad 2.7. Určete
Řešení. (Obr. Komplexní čísla 2).
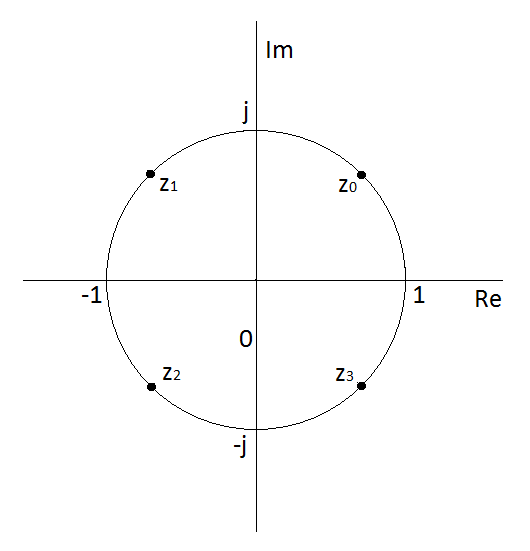
Příklad 2.8. Určete
Řešení. (Obr. Komplexní čísla 3).
 |
 |
|
Obr. 2. Řešení příkladu Komplexní čísla 2.7.
|
Obr. 3. Řešení příkladu Komplexní čísla 2.8.
|




