
3.1 Korelační koeficient
Míru korelace mezi hodnotami dvou statických1 veličin (vektorů) určujeme pomocí korelačních koeficientů. Způsob jejich výpočtu závisí na charakteru veličin, jejichž vztah zkoumáme.
V případě, že veličiny a
jsou náhodné kvantitativní veličiny, pak pro dvojice realizací
je hodnota tzv. Pearsonova korelačního koeficientu dána vztahem
| (12) |
Díky standardizaci vzhledem ke standardní odchylce se hodnoty Pearsonova korelačního koeficientu pohybují v intervalu Obě mezní hodnoty znamenají přesný lineární vztah. V případě
se jedná o nepřímou závislost, tj. s růstem hodnot jedné z proměnných hodnoty druhé proměnné klesají (funkční vztah má zápornou směrnici), pro
je úměra přímá, s růstem hodnot jedné proměnné rostou hodnoty i druhé proměnné (funkční vztah má kladnou směrnici). V případě, že veličiny mají vzájemné dvourozměrné normální rozložení, pak nulová hodnota korelačního koeficientu znamená i nezávislost obou veličin. Pokud ale tento předpoklad není splněn (a nutno říci, že v praxi se tento předpoklad ne vždy ověřuje), pak o obou veličinách nemůžeme říci více, než jen, že jsou nekorelované.
Hodnoty Pearsonova korelačního koeficientu mohou být nesplněním předpokladu o vzájemné dvourozměrné normalitě náhodných veličin a
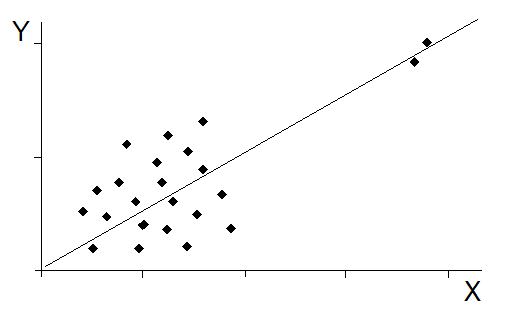
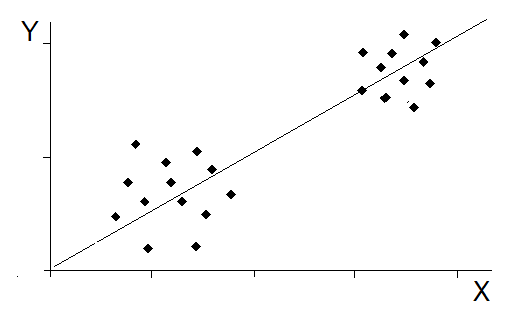
nepříznivě ovlivněny (nadhodnoceny), např. při přítomnosti odlehlých hodnot, pokud jsou data rozdělena do shluků, nebo i vlivem další skryté veličiny (obr. Modely veličin spojitých v čase II 6).
 |
 |
|
a)
|
b)
|
|
Obr. 6. Příčiny možného nadhodnocení Pearsonova korelačního koeficientu – a) vlivem odlehlých hodnot; b) vlivem shluků
|
|
Existují i další způsoby posouzení, resp. kvantizace vzájemného vztahu dvou náhodných veličin pro různé podmínky, příp. vlastnosti experimentálních veličin. Zde však vystačíme s uvedeným Pearsonovým koeficientem, protože s ním je možné srovnat způsob hodnocení dynamické vazby časově proměnných veličin.
1 Statická data nezávisí na čase, ani na žádné další veličině – pořadí, v jakém jsou seřazena, není v jádru důležité; data nejsou tzv. uspořádaná. Popisují určitý objekt, jehož stav se nemění, nebo jehož změny nejsou z hlediska analýzy podstatné. Typickým příkladem jsou např. pacientské registry, nebo soubory popisných dat, které slouží ke klasifikaci rostlin nebo živočichů, příp. pacientské záznamy, na základě kterých se stanoví diagnóza.




