E-learningová učebnice

Matematická biologie

Slovník | Vyhledávání | Mapa webu

Analýza a modelování dynamických biologických datSignály a lineární systémy Časové řady II 2 Fourierova transformace s diskrétním časem (DTFT)

Lineární a adaptivní zpracování dat | Lineární a adaptivní zpracování dat: řešené úlohy v MATLABu | Matematické modely v biologii | Maticové populační modely | Signály a lineární systémy |

Kapitola počáteční |

Výstupy z výukové jednotky | 1 Začínáme – několik ilustračních příkladů na úvod | 2 Nejdůležitější pojmy |

2.1 Signál, veličina, funkce, časová řada | 2.2 Systém |

Modely veličin spojitých v čase I |

Výstupy z výukové jednotky | 1 Základní typy matematických modelů veličin spojitých v čase |

1.1 Periodické funkce |

1.1.1 Harmonická funkce |

1. 2 Neperiodické funkce |

1.2.1 Deterministické jednorázové funkce | 1.2.2 Náhodné funkce |

2 Základní unární operace s funkcemi se spojitým časem |

Modely veličin spojitých v čase II |

Výstupy z výukové jednotky | 1 Konvoluce | 2 Kauzalita | 3 Korelace |

3.1 Korelační koeficient | 3.2 Korelační funkce |

Modely veličin spojitých v čase III |

Výstupy z výukové jednotky | 1 Rozklad spojitých periodických funkcí na dílčí harmonické složky |

1.1 Proč? | 1.2 Fourierova řada |

2 Rozklad spojitých neperiodických funkcí na dílčí harmonické složky – Fourierova transformace |

2.1 Definice | 2.2 Vlastnosti Fourierovy transformace | 2.3 Několik řešených příkladů | 2.4 A na konec ještě pár příkladů k procvičení |

Časové řady I |

Výstupy z výukové jednotky | 1 Vzorkování |

1.1 Seznamme se | 1.2 Vzorkovací teorém |

2 Základní typy matematických modelů veličin diskrétních v čase |

2.1 Konvence na začátek | 2.2 Periodické posloupnosti | 2.3 Jednorázové posloupnosti |

3 Základní operace s matematickými modely veličin diskrétních v čase |

3.1 Úvodní poznámky | 3.2 Diskrétní konvoluce | 3.3 Diskrétní korelační posloupnost |

Časové řady II |

Výstupy z výukové jednotky | 1 Diskrétní Fourierova řada | 2 Fourierova transformace s diskrétním časem (DTFT) | 3 Diskrétní Fourierova transformace (DFT) | 4 Rychlá Fourierova transformace (FFT) | 5 Rekonstrukce spojité funkce z navzorkované posloupnosti |

Matematický popis systémů pracujících ve spojitém čase I |

Výstupy z výukové jednotky | 1 Linearita | 2 Vnější (vstupní/výstupní) popis lineárních systémů |

2.1 Lineární diferenciální rovnice |

3 Laplacova transformace |

3.1 Zavedení Laplacovy transformace | 3.2 Důležité vlastnosti Laplacovy transformace |

4 Vnější (vstupní/výstupní) popis - pokračování |

4.1 Obrazová přenosová funkce | 4.2 Rozložení nulových bodů a pólů operátorové přenosové funkce | 4.3 Frekvenční přenosová funkce a frekvenční charakteristiky | 4.4 Impulzní charakteristika | 4.5 Přechodová charakteristika | 4.6 Vzájemné vztahy mezi různými formami vnějšího popisu lineárního systému |

Matematický popis systémů pracujících ve spojitém čase II |

Výstupy z výukové jednotky | 1 Vnější popis nelineárních systémů | 2 Vnitřní (stavový) popis |

2.1 Lineární případ | 2.2 Nelineární případ |

3 Chování systémů |

3.1 Základní jevy v systémech |

4 Stabilita |

4.1 Základní pojmy | 4.2 Zkoumání stability | 4.3 Zobecněná stabilita dle Ljapunova |

5 Kauzalita |

Matematický popis lineárních systémů pracujících v diskrétním čase |

Výstupy z výukové jednotky | 1 Vnější (vstupní/výstupní) popis |

1.1 Diferenční rovnice |

2 Transformace Z |

2.1 Zavedení transformace Z | 2.2 Důležité vlastnosti transformace Z |

3 Vnější (vstupní/výstupní) popis - pokračování |

3.1 Obrazová přenosová funkce | 3.2 Rozložení nulových bodů a pólů obrazové přenosové funkce | 3.3 Frekvenční přenosová funkce a frekvenční charakteristiky | 3.4 Časové charakteristiky |

4. Vnitřní (stavový) popis | 5 Stabilita |

Systémové struktury |

Výstupy z výukové jednotky | 1 Základní formy spojování systémů | 2 Sériové (kaskádní) zapojení | 3 Paralelní zapojení | 4 Zpětnovazební zapojení |

4.3 Princip zpětnovazební regulace | 4.1 Popis přenosu zpětnovazebního systému | 4.2 Vlastnosti zpětnovazebního zapojení |

Komplexní čísla |

Výstupy z výukové jednotky | Základní typy popisu komplexních čísel | Matematické operace s komplexními čísly | Komplexní exponenciála |

Spojité deterministické modely I | Diskrétní deterministické modely | Úvod do matematického modelování | Vybrané kapitoly z matematického modelování |

2 Fourierova transformace s diskrétním časem (DTFT)

Pokusme se zde uplatnit podobnou strategii jako v případě přechodu od Fourierovy řady k Fourierově transformaci v případě funkcí spojitých v čase

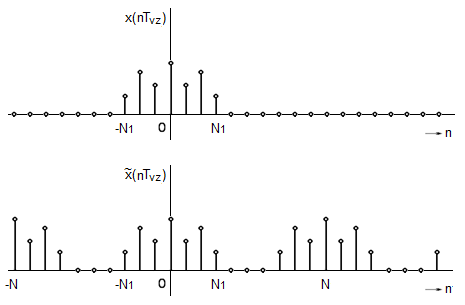
Definice 2.1. Nechť je časově omezená posloupnost s diskrétním časem s pro všechna celá a kde je celočíselná konstanta. Dále, nechť pro jakékoliv kladné celé sudé číslo označíme posloupnost s periodou která je pro (obr. Časové řady II 2)

Z definice máme

Protože je periodická funkce s periodou má Fourierovu řadu

kde

Z vlastností vyplývá, že lze poslední uvedenou rovnici přepsat do tvaru

a potom

kde je pro spojitá (nediskrétní) veličina.

Obr. 2. Podmínky přechodu od diskrétní Fourierovy řady k Fourierově transformaci

Úvahy z výše uvedené definice jen potvrzují, co už známe z rozkladu spojitých funkcí, totiž že spojitost či nespojitost spektra nesouvisí se spojitostí či nespojitostí rozkládané funkce, nýbrž s její periodičností.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity