E-learningová učebnice

Matematická biologie

Slovník | Vyhledávání | Mapa webu

Analýza a modelování dynamických biologických datSignály a lineární systémy Časové řady II 5 Rekonstrukce spojité funkce z navzorkované posloupnosti

Lineární a adaptivní zpracování dat | Lineární a adaptivní zpracování dat: řešené úlohy v MATLABu | Matematické modely v biologii | Maticové populační modely | Signály a lineární systémy |

Kapitola počáteční |

Výstupy z výukové jednotky | 1 Začínáme – několik ilustračních příkladů na úvod | 2 Nejdůležitější pojmy |

2.1 Signál, veličina, funkce, časová řada | 2.2 Systém |

Modely veličin spojitých v čase I |

Výstupy z výukové jednotky | 1 Základní typy matematických modelů veličin spojitých v čase |

1.1 Periodické funkce |

1.1.1 Harmonická funkce |

1. 2 Neperiodické funkce |

1.2.1 Deterministické jednorázové funkce | 1.2.2 Náhodné funkce |

2 Základní unární operace s funkcemi se spojitým časem |

Modely veličin spojitých v čase II |

Výstupy z výukové jednotky | 1 Konvoluce | 2 Kauzalita | 3 Korelace |

3.1 Korelační koeficient | 3.2 Korelační funkce |

Modely veličin spojitých v čase III |

Výstupy z výukové jednotky | 1 Rozklad spojitých periodických funkcí na dílčí harmonické složky |

1.1 Proč? | 1.2 Fourierova řada |

2 Rozklad spojitých neperiodických funkcí na dílčí harmonické složky – Fourierova transformace |

2.1 Definice | 2.2 Vlastnosti Fourierovy transformace | 2.3 Několik řešených příkladů | 2.4 A na konec ještě pár příkladů k procvičení |

Časové řady I |

Výstupy z výukové jednotky | 1 Vzorkování |

1.1 Seznamme se | 1.2 Vzorkovací teorém |

2 Základní typy matematických modelů veličin diskrétních v čase |

2.1 Konvence na začátek | 2.2 Periodické posloupnosti | 2.3 Jednorázové posloupnosti |

3 Základní operace s matematickými modely veličin diskrétních v čase |

3.1 Úvodní poznámky | 3.2 Diskrétní konvoluce | 3.3 Diskrétní korelační posloupnost |

Časové řady II |

Výstupy z výukové jednotky | 1 Diskrétní Fourierova řada | 2 Fourierova transformace s diskrétním časem (DTFT) | 3 Diskrétní Fourierova transformace (DFT) | 4 Rychlá Fourierova transformace (FFT) | 5 Rekonstrukce spojité funkce z navzorkované posloupnosti |

Matematický popis systémů pracujících ve spojitém čase I |

Výstupy z výukové jednotky | 1 Linearita | 2 Vnější (vstupní/výstupní) popis lineárních systémů |

2.1 Lineární diferenciální rovnice |

3 Laplacova transformace |

3.1 Zavedení Laplacovy transformace | 3.2 Důležité vlastnosti Laplacovy transformace |

4 Vnější (vstupní/výstupní) popis - pokračování |

4.1 Obrazová přenosová funkce | 4.2 Rozložení nulových bodů a pólů operátorové přenosové funkce | 4.3 Frekvenční přenosová funkce a frekvenční charakteristiky | 4.4 Impulzní charakteristika | 4.5 Přechodová charakteristika | 4.6 Vzájemné vztahy mezi různými formami vnějšího popisu lineárního systému |

Matematický popis systémů pracujících ve spojitém čase II |

Výstupy z výukové jednotky | 1 Vnější popis nelineárních systémů | 2 Vnitřní (stavový) popis |

2.1 Lineární případ | 2.2 Nelineární případ |

3 Chování systémů |

3.1 Základní jevy v systémech |

4 Stabilita |

4.1 Základní pojmy | 4.2 Zkoumání stability | 4.3 Zobecněná stabilita dle Ljapunova |

5 Kauzalita |

Matematický popis lineárních systémů pracujících v diskrétním čase |

Výstupy z výukové jednotky | 1 Vnější (vstupní/výstupní) popis |

1.1 Diferenční rovnice |

2 Transformace Z |

2.1 Zavedení transformace Z | 2.2 Důležité vlastnosti transformace Z |

3 Vnější (vstupní/výstupní) popis - pokračování |

3.1 Obrazová přenosová funkce | 3.2 Rozložení nulových bodů a pólů obrazové přenosové funkce | 3.3 Frekvenční přenosová funkce a frekvenční charakteristiky | 3.4 Časové charakteristiky |

4. Vnitřní (stavový) popis | 5 Stabilita |

Systémové struktury |

Výstupy z výukové jednotky | 1 Základní formy spojování systémů | 2 Sériové (kaskádní) zapojení | 3 Paralelní zapojení | 4 Zpětnovazební zapojení |

4.3 Princip zpětnovazební regulace | 4.1 Popis přenosu zpětnovazebního systému | 4.2 Vlastnosti zpětnovazebního zapojení |

Komplexní čísla |

Výstupy z výukové jednotky | Základní typy popisu komplexních čísel | Matematické operace s komplexními čísly | Komplexní exponenciála |

Spojité deterministické modely I | Diskrétní deterministické modely | Úvod do matematického modelování | Vybrané kapitoly z matematického modelování |

5 Rekonstrukce spojité funkce z navzorkované posloupnosti

Pro ty, kterým nedá spát, jak se z teoreticky nekonečné navzorkované posloupnosti můžeme dostat zpět k spojité funkci, uvádíme jedno malé teoretické odvození.

Předpokládejme, že původní spojitá funkce měla frekvenčně omezené spektrum tj. platí pro ni

kde je frekvenční spektrum dané posloupnosti. Protože víme, že navzorkovaná posloupnost je periodická s periodou danou vzorkovací frekvencí, zajímá nás pouze její jedna (první) perioda, pro kterou v rozsahu frekvencí platí

Potom pro původní funkci je

	(28)

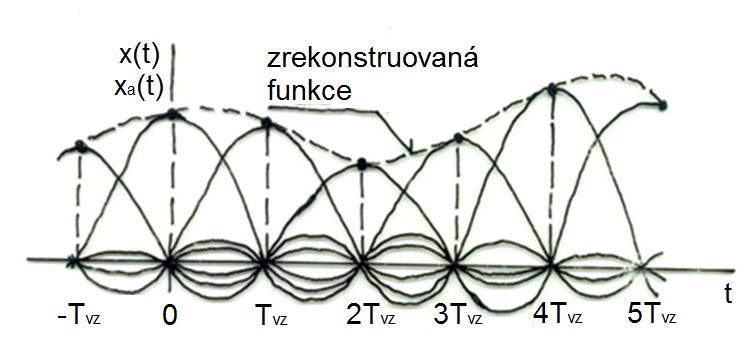
Co tento vztah říká? Původní funkce je dána nekonečným součtem vzorkovacích funkcí, které procházejí každou hodnotou z nekonečného počtu vzorků navzorkované posloupnosti. Přesně tak, jak ukazuje následující obrázek.

Obr. 7. Rekonstrukce navzorkované posloupnosti

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity