4.6 Vzájemné vztahy mezi různými formami vnějšího popisu lineárního systému

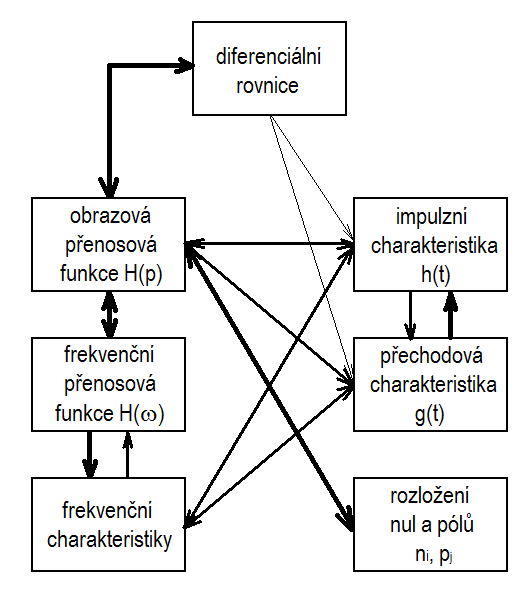
Na obr. Matematický popis systémů pracujících ve spojitém čase I 6 je zobrazeno všech sedm dříve uvedených způsobů vnějšího popisu lineárních systémů. Používané vzájemné převody jsou v obrázku vyznačeny spojnicemi mezi jednotlivými způsoby popisu, čím jednodušší a používanější převod, tím je spojnice mezi popisy silněji vyznačena. Obecně lze konstatovat, že všechny způsoby vnějšího popisu lineárních systémů jsou si vzájemně ekvivalentní (kromě rozložení nul a pólů), je jen otázka jak potřeba, jak praktické a jak obtížné jsou vzájemné převody.

Obr. 6. Vzájemné převody různých forem vnějšího popisu lineárních systémů

Mnohé z těchto převodů jsme uvedli v kapitolách pojednávajících o jednotlivých formách popisu. Elementární a velice často používaný je převod mezi diferenciální rovnicí a obrazovou přenosovou funkcí, vycházející z Laplacova obrazu derivace. Podobná situace je převodem obrazové přenosové funkce na frekvenční přenosovou funkci a naopak, resp. dále na frekvenční charakteristiky. Obtížnější je určení analytické přenosové funkce (frekvenční, obrazové) z naměřených hodnot frekvenčních charakteristik, většinou se tak děje přibližnou aproximací, je-li zadán předpokládaný či známý řád systému nebo alespoň požadavek na přesnost aproximace. Jednoduchý je i převod mezi časovými charakteristikami (impulzní charakteristika je derivací přechodové charakteristiky) a převod mezi časovými charakteristikami a přenosovými funkcemi. Vztahy mezi frekvenční a časovou oblastí již tak jednoduché nejsou.