Analýza a modelování dynamických biologických datSignály a lineární systémy Modely veličin spojitých v čase I 1 Základní typy matematických modelů veličin spojitých v čase 1.1 Periodické funkce

Kapitola počáteční |

Výstupy z výukové jednotky | 1 Začínáme – několik ilustračních příkladů na úvod | 2 Nejdůležitější pojmy |

2.1 Signál, veličina, funkce, časová řada | 2.2 Systém |

Modely veličin spojitých v čase I |

Výstupy z výukové jednotky | 1 Základní typy matematických modelů veličin spojitých v čase |

1.1 Periodické funkce |

1.1.1 Harmonická funkce |

1. 2 Neperiodické funkce |

1.2.1 Deterministické jednorázové funkce | 1.2.2 Náhodné funkce |

2 Základní unární operace s funkcemi se spojitým časem |

Modely veličin spojitých v čase II |

Výstupy z výukové jednotky | 1 Konvoluce | 2 Kauzalita | 3 Korelace |

3.1 Korelační koeficient | 3.2 Korelační funkce |

Modely veličin spojitých v čase III |

Výstupy z výukové jednotky | 1 Rozklad spojitých periodických funkcí na dílčí harmonické složky |

1.1 Proč? | 1.2 Fourierova řada |

2 Rozklad spojitých neperiodických funkcí na dílčí harmonické složky – Fourierova transformace |

2.1 Definice | 2.2 Vlastnosti Fourierovy transformace | 2.3 Několik řešených příkladů | 2.4 A na konec ještě pár příkladů k procvičení |

Časové řady I |

Výstupy z výukové jednotky | 1 Vzorkování |

1.1 Seznamme se | 1.2 Vzorkovací teorém |

2 Základní typy matematických modelů veličin diskrétních v čase |

2.1 Konvence na začátek | 2.2 Periodické posloupnosti | 2.3 Jednorázové posloupnosti |

3 Základní operace s matematickými modely veličin diskrétních v čase |

3.1 Úvodní poznámky | 3.2 Diskrétní konvoluce | 3.3 Diskrétní korelační posloupnost |

Časové řady II |

Matematický popis systémů pracujících ve spojitém čase I |

Výstupy z výukové jednotky | 1 Linearita | 2 Vnější (vstupní/výstupní) popis lineárních systémů |

2.1 Lineární diferenciální rovnice |

3 Laplacova transformace |

3.1 Zavedení Laplacovy transformace | 3.2 Důležité vlastnosti Laplacovy transformace |

4 Vnější (vstupní/výstupní) popis - pokračování |

4.1 Obrazová přenosová funkce | 4.2 Rozložení nulových bodů a pólů operátorové přenosové funkce | 4.3 Frekvenční přenosová funkce a frekvenční charakteristiky | 4.4 Impulzní charakteristika | 4.5 Přechodová charakteristika | 4.6 Vzájemné vztahy mezi různými formami vnějšího popisu lineárního systému |

Matematický popis systémů pracujících ve spojitém čase II |

Výstupy z výukové jednotky | 1 Vnější popis nelineárních systémů | 2 Vnitřní (stavový) popis |

2.1 Lineární případ | 2.2 Nelineární případ |

3 Chování systémů |

3.1 Základní jevy v systémech |

4 Stabilita |

4.1 Základní pojmy | 4.2 Zkoumání stability | 4.3 Zobecněná stabilita dle Ljapunova |

5 Kauzalita |

Matematický popis lineárních systémů pracujících v diskrétním čase |

Výstupy z výukové jednotky | 1 Vnější (vstupní/výstupní) popis |

1.1 Diferenční rovnice |

2 Transformace Z |

2.1 Zavedení transformace Z | 2.2 Důležité vlastnosti transformace Z |

3 Vnější (vstupní/výstupní) popis - pokračování |

3.1 Obrazová přenosová funkce | 3.2 Rozložení nulových bodů a pólů obrazové přenosové funkce | 3.3 Frekvenční přenosová funkce a frekvenční charakteristiky | 3.4 Časové charakteristiky |

4. Vnitřní (stavový) popis | 5 Stabilita |

Systémové struktury |

4.3 Princip zpětnovazební regulace | 4.1 Popis přenosu zpětnovazebního systému | 4.2 Vlastnosti zpětnovazebního zapojení |

Komplexní čísla |

Výstupy z výukové jednotky | Základní typy popisu komplexních čísel | Matematické operace s komplexními čísly | Komplexní exponenciála |

Spojité deterministické modely I | Diskrétní deterministické modely | Úvod do matematického modelování | Vybrané kapitoly z matematického modelování |

1.1 Periodické funkce

Definice 1.2. Spojitá jednorozměrná funkce je periodická, když existuje takové číslo pro které a pro všechny reálné hodnoty je

(1)

kde je libovolné celé číslo. Nejmenší hodnotu (pokud taková hodnota existuje), pro kterou platí rovnice Modely veličin spojitých v čase I (1) nazýváme základní periodou funkce.

Všechny funkce, které nesplňují vztah Modely veličin spojitých v čase I (1) nejsou periodické, tj. jsou neperiodické.

Také lze použít definice a v dalším textu si takovou představou občas vypomůžeme, že neperiodická funkce je taková periodická funkce, jejíž základní perioda je nekonečná, tj. platí pouze pro

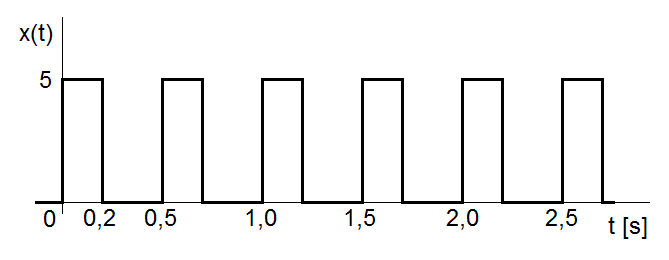
Příklad 1.3. Rozhodněte, zda je funkce (obr. Modely veličin spojitých v čase I 1)

(2)

kde je libovolné celé číslo, periodická či nikoliv.

Obr. 1. Periodický funkce podle vztahu Modely veličin spojitých v čase I (2)

Řešení. Z definičního vztahu, vyplývá, že každá z obou úrovní funkce se opakuje po [s]. Proto je funkce periodická a její základní perioda je s.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity