Analýza a modelování dynamických biologických datSignály a lineární systémy Časové řady II 3 Diskrétní Fourierova transformace (DFT)

Kapitola počáteční |

Výstupy z výukové jednotky | 1 Začínáme – několik ilustračních příkladů na úvod | 2 Nejdůležitější pojmy |

2.1 Signál, veličina, funkce, časová řada | 2.2 Systém |

Modely veličin spojitých v čase I |

Výstupy z výukové jednotky | 1 Základní typy matematických modelů veličin spojitých v čase |

1.1 Periodické funkce |

1.1.1 Harmonická funkce |

1. 2 Neperiodické funkce |

1.2.1 Deterministické jednorázové funkce | 1.2.2 Náhodné funkce |

2 Základní unární operace s funkcemi se spojitým časem |

Modely veličin spojitých v čase II |

Výstupy z výukové jednotky | 1 Konvoluce | 2 Kauzalita | 3 Korelace |

3.1 Korelační koeficient | 3.2 Korelační funkce |

Modely veličin spojitých v čase III |

Výstupy z výukové jednotky | 1 Rozklad spojitých periodických funkcí na dílčí harmonické složky |

1.1 Proč? | 1.2 Fourierova řada |

2 Rozklad spojitých neperiodických funkcí na dílčí harmonické složky – Fourierova transformace |

2.1 Definice | 2.2 Vlastnosti Fourierovy transformace | 2.3 Několik řešených příkladů | 2.4 A na konec ještě pár příkladů k procvičení |

Časové řady I |

Výstupy z výukové jednotky | 1 Vzorkování |

1.1 Seznamme se | 1.2 Vzorkovací teorém |

2 Základní typy matematických modelů veličin diskrétních v čase |

2.1 Konvence na začátek | 2.2 Periodické posloupnosti | 2.3 Jednorázové posloupnosti |

3 Základní operace s matematickými modely veličin diskrétních v čase |

3.1 Úvodní poznámky | 3.2 Diskrétní konvoluce | 3.3 Diskrétní korelační posloupnost |

Časové řady II |

Matematický popis systémů pracujících ve spojitém čase I |

Výstupy z výukové jednotky | 1 Linearita | 2 Vnější (vstupní/výstupní) popis lineárních systémů |

2.1 Lineární diferenciální rovnice |

3 Laplacova transformace |

3.1 Zavedení Laplacovy transformace | 3.2 Důležité vlastnosti Laplacovy transformace |

4 Vnější (vstupní/výstupní) popis - pokračování |

4.1 Obrazová přenosová funkce | 4.2 Rozložení nulových bodů a pólů operátorové přenosové funkce | 4.3 Frekvenční přenosová funkce a frekvenční charakteristiky | 4.4 Impulzní charakteristika | 4.5 Přechodová charakteristika | 4.6 Vzájemné vztahy mezi různými formami vnějšího popisu lineárního systému |

Matematický popis systémů pracujících ve spojitém čase II |

Výstupy z výukové jednotky | 1 Vnější popis nelineárních systémů | 2 Vnitřní (stavový) popis |

2.1 Lineární případ | 2.2 Nelineární případ |

3 Chování systémů |

3.1 Základní jevy v systémech |

4 Stabilita |

4.1 Základní pojmy | 4.2 Zkoumání stability | 4.3 Zobecněná stabilita dle Ljapunova |

5 Kauzalita |

Matematický popis lineárních systémů pracujících v diskrétním čase |

Výstupy z výukové jednotky | 1 Vnější (vstupní/výstupní) popis |

1.1 Diferenční rovnice |

2 Transformace Z |

2.1 Zavedení transformace Z | 2.2 Důležité vlastnosti transformace Z |

3 Vnější (vstupní/výstupní) popis - pokračování |

3.1 Obrazová přenosová funkce | 3.2 Rozložení nulových bodů a pólů obrazové přenosové funkce | 3.3 Frekvenční přenosová funkce a frekvenční charakteristiky | 3.4 Časové charakteristiky |

4. Vnitřní (stavový) popis | 5 Stabilita |

Systémové struktury |

4.3 Princip zpětnovazební regulace | 4.1 Popis přenosu zpětnovazebního systému | 4.2 Vlastnosti zpětnovazebního zapojení |

Komplexní čísla |

Výstupy z výukové jednotky | Základní typy popisu komplexních čísel | Matematické operace s komplexními čísly | Komplexní exponenciála |

Spojité deterministické modely I | Diskrétní deterministické modely | Úvod do matematického modelování | Vybrané kapitoly z matematického modelování |

3 Diskrétní Fourierova transformace (DFT)

Aby bylo možné s frekvenčním spektrem prakticky počítat, je užitečné spektrální funkci diskretizovat.

Definice 3.1. Předpokládejme, že posloupnost pro a pak DFT je definována vztahem

	(14)

Definice 3.2. Zpětnou inverzní diskrétní Fourierovu transformaci pak definuje vztah

(15)

Definice 3.3. Pokud uvažujeme pouze posloupnost hodnot bez její časové resp. kmitočtové interpretace, lze definiční vztah diskrétní Fourierovy transformace vyjádřit též ve tvaru

(16)

resp. inverzní transformace

(17)

Diskrétní Fourierova transformace, stejně jako všechny ostatní formy Fourierovy transformace, je inverzibilní, tj. platí:

(18)

což lze dokázat následovně:

		(19)

Protože podobně jako v důkazu diskrétní Fourierovy řady je pro a pro je můžeme pokračovat

(20)

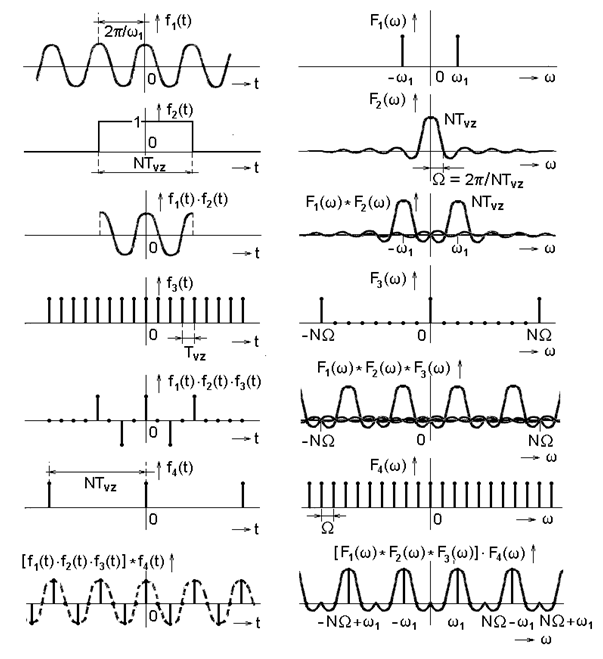
Obr. 3. Princip a důsledky diskrétní Fourierovy transformace pro kmitočet signálu ω₁ = ω_vz/4 = /(2T_vz)

Vliv DFT na charakter spektra harmonické posloupnosti je patrný z obr. Časové řady II 3 a Časové řady II 4. Na obr. Časové řady II 3 je zobrazen případ, kdy je perioda vzorkované funkce rovna celočíselnému násobku vzorkovací periody v konkrétním případě tj. Na obou obrázcích jsou zobrazeny v levé části časové průběhy a vpravo jim odpovídající spektra. Konečný úsek signálu je vytvořen z původního časově neomezeného průběhu vynásobením obdélníkovým oknem, jehož délka je rovna celočíselnému násobku vzorkovací periody, konkrétně Spektrum vynásobeného, tj. časově omezeného úseku spojité harmonické funkceje dán konvolucí spekter původního harmonického signálu a spektra obdélníkového okna ve tvaru funkce Vzorkování tohoto úseku funkce o konečné době trvání vyjádříme dle definice Časové řady I 1.2 násobením sledem jednotkových impulsů s periodou opakování rovnou vzorkovací periodě Tomu odpovídá rovněž periodické impulsní spektrum s periodou rovnou vzorkovací frekvenci a výsledné spektrum navzorkované posloupnosti je konvolucí všech tří dílčích složek, jejichž násobením vznikl diskrétní harmonický signál omezeného trvání.

Diskrétní verzi spektra získáme násobením spektra pulsem Diracových s frekvencí Tomuto pulsu odpovídá v časové oblasti periodický sled jednotkových impulsů s periodou Protože konečné spektrum je výsledkem násobení spojitého spektra navzorkované posloupnosti konečného trvání, je časová reprezentace navzorkovaného spektra konvoluce navzorkované posloupnosti s časovou reprezentací vzorkovacího pulsu spektra. Touto konvolucí se posloupnosti nepřímo vnucuje periodicita, takže výsledné diskrétní spektrum je spektrem periodické posloupnosti. Tím, že je vzorkování signálu vhodně vázáno s délkou konečného obdélníkového okna a tím i se vzorkováním spektra, odpovídá fiktivní výsledná periodická posloupnost původní funkci, jejíž spektrum jsme pomocí DFT počítali.

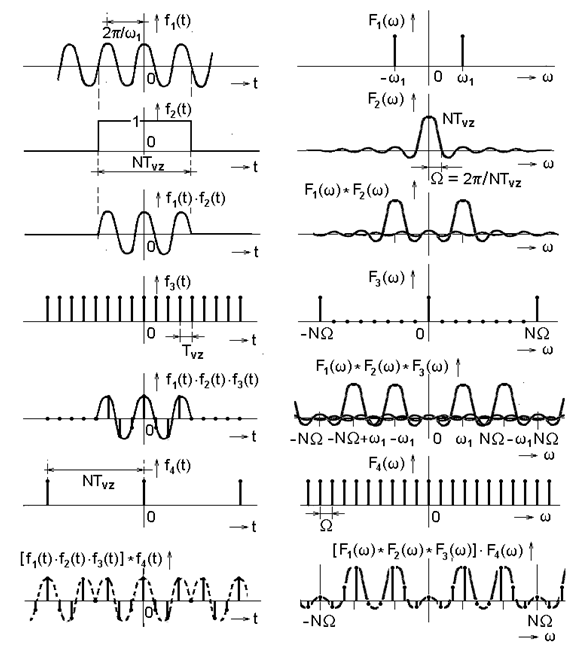
Na druhé straně, pokud délka omezujícího obdélníkového okna neodpovídá celočíselnému násobku period vstupního signálu, pak i výsledné diskrétní spektrum odpovídá funkci, jejíž průběh je modifikován, např. tak, jak je zobrazeno na obr. Časové řady II 4.

Druhý, zřejmě ještě důležitější důsledek formální diskretizace spektrální funkce a z toho vyplývající vnucené periodizace transformované posloupnosti je ten, že diskrétní Fourierova transformace je téměř totožná s diskrétní Fourierovou řadou. Jediný rozdíl je v dělení počtem vzorků v periodě při výpočtu komplexních koeficientů, jejichž moduly udávají amplitudy harmonických složek odpovídající frekvence a jejich argumenty počáteční fázi. Protože definiční vztah DFT toto dělení neobsahuje, neodpovídají výsledné hodnoty amplitudám harmonických složek, ale hodnotám -krát větším.

Obr. 4. Princip a důsledky diskrétní Fourierovy transformace pro kmitočet signálu ω₁ =5 ω_vz/16 = 5/(8T_vz)

Příklad 3.4. Mějme zadánu posloupnost čtyř nenulových vzorků a všechny ostatní hodnoty pro Určete hodnoty vzorků frekvenčního spektra pro

Řešení. Definiční vztah Časové řady II (16) pro diskrétní Fourierovu transformaci

Lze přeformulovat i do trigonometrického tvaru

Z tohoto tvaru lze snadno vyjádřit reálné a imaginární části komplexních hodnot vzorků spektra

a

Po dosazení za k dostáváme

Z toho jsou hodnoty vzorků frekvenčního spektra v kartézském tvaru

a v polárním tvaru, který je v tomto případě běžnější je

Z dosažených výsledků je zřejmé, že posloupnost modulů spektrálních hodnot (čar) je symetrická s osou symetrie pro a antisymetrická s toutéž osou pokud jde o argumenty (fáze) spektrálních hodnot. Posloupnost by byla periodická, pro hodnoty by se hodnoty spektrálních vzorků opakovaly.

Pokud bychom chtěli, aby moduly odpovídaly amplitudám odpovídajících harmonických složek, musíme vypočítané hodnoty podělit počtem vzorků, tedy čtyřmi. Správnost takového počínání snadno ověříme pro které po podělení vychází což právě odpovídá střední hodnotě ze čtyř nenulových vzorků zadané posloupnosti.

Příklad 3.5. Určete hodnoty spektrálních vzorků posloupnosti

Řešení. Nejdříve jednoduchá úvaha. Všechny zadané vzorky nabývají stejné hodnoty. Zadání tedy odpovídá periodicky se opakující hodnotě 1 s periodou 4. Protože data neobsahují žádnou jinou periodicitu, spektrum by mělo obsahovat pouze jeden nenulový vzorek a to pro nulovou frekvenci, tj. stejnosměrnou složku.

Použijeme-li téhož postupu jako v předchozím příkladu Časové řady II 3.4, dostáváme hodnoty spektrálních čar: a Spektrální hodnota pro nulovou frekvenci je tedy opravdu rovna čtyřnásobku amplitudy harmonické složky s nulovou frekvencí.



Příklad 3.6. Určete hodnoty spektrálních vzorků posloupnosti

Řešení. Nejdříve opět jednoduchá úvaha. Zadané vzorky odpovídají jednotkovému impulzu a protože prostřednictvím DFT vnucujeme posloupnosti periodicitu s periodou odpovídající počtu zadaných vzorků, reprezentují zadané hodnoty periodický sled jednotkových impulzů s periodou čtyři vzorky. Protože spektrum jednotkového impulzu je konstantní (harmonické složky jsou zastoupeny rovnoměrně, tj s toutéž amplitudou. Moduly spektrálních vzorků by tedy měly po výpočtu pomocí DFT být a po podělení počtem vzorků Ověřte si výpočtem opět podle postupu v příkladu Časové řady II 3.4.

Příklad 3.7. Určete hodnoty spektrálních vzorků posloupnosti a vysvětlete charakter vypočítaného spektra.

Řešení. pro což lze též vyjádřit a normalizovaná posloupnost na jeden vzorek Výslednou posloupnost lze interpretovat tak, že data obsahují harmonickou složku o periodě rovné počtu vzorků v posloupnosti (tzv. první harmonická složka) o amplitudě a počáteční fázi – logicky, protože data začínají od 0, vzorky tedy odpovídají sinusovce, který je vůči referenční funkci kosinus posunutá právě o úhel

Příklad 3.8. Co by se stalo, kdyby se posloupnost z příkladu Časové řady II 3.7 posunula o jeden vzorek, tj. byla by

Řešení. Po aplikaci postupu z příkladu Časové řady II 3.4 dostáváme pro To znamená, že počáteční fáze první harmonické je nulová. Jak jinak, když datová posloupnost začíná jedničkou a odpovídá tak referenčnímu kosinu.

Příklad 3.9. Určete hodnoty spektrálních vzorků posloupnosti a vysvětlete charakter vypočítaného spektra.

Řešení. pro a pro Zadaná datová posloupnost obsahuje dvě periody, tj. dvojnásobek základní periody dané počtem vzorků datové posloupnosti. Tato frekvence (druhá harmonická složka) je rovna polovině vzorkovací frekvence (4 vzorky v posloupnosti). Pro tuto frekvenci nemá spektrální posloupnost dva vzorky, nýbrž pouze jeden ležící na záporné reálné ose v komplexní rovině, proto je jeho hodnota dvojnásobná, než jak jsme sdi zvykli v předcházejících příkladech.

Příklad 3.10. Pokud by se datová posloupnost posunula o jeden vzorek ve srovnání s předešlým příkladem, tj. byla by znamenalo by to, že se druhá harmonická složka posunula o polovinu periody. Jak by se to projevili ve spektrální posloupnosti?

Řešení

Příklad 3.11. Bylo by možné v datové i spektrální posloupnosti zobrazit harmonickou funkci s periodou rovnou třetině délky datové posloupnosti?

Řešení

Harmonická složka má frekvenci, která je již větší, než vzorkovací frekvence. V datové posloupnosti by se zobrazila jako první harmonická.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity