Analýza a modelování dynamických biologických datSignály a lineární systémy Modely veličin spojitých v čase I 2 Základní unární operace s funkcemi se spojitým časem

Kapitola počáteční |

Výstupy z výukové jednotky | 1 Začínáme – několik ilustračních příkladů na úvod | 2 Nejdůležitější pojmy |

2.1 Signál, veličina, funkce, časová řada | 2.2 Systém |

Modely veličin spojitých v čase I |

Výstupy z výukové jednotky | 1 Základní typy matematických modelů veličin spojitých v čase |

1.1 Periodické funkce |

1.1.1 Harmonická funkce |

1. 2 Neperiodické funkce |

1.2.1 Deterministické jednorázové funkce | 1.2.2 Náhodné funkce |

2 Základní unární operace s funkcemi se spojitým časem |

Modely veličin spojitých v čase II |

Výstupy z výukové jednotky | 1 Konvoluce | 2 Kauzalita | 3 Korelace |

3.1 Korelační koeficient | 3.2 Korelační funkce |

Modely veličin spojitých v čase III |

Výstupy z výukové jednotky | 1 Rozklad spojitých periodických funkcí na dílčí harmonické složky |

1.1 Proč? | 1.2 Fourierova řada |

2 Rozklad spojitých neperiodických funkcí na dílčí harmonické složky – Fourierova transformace |

2.1 Definice | 2.2 Vlastnosti Fourierovy transformace | 2.3 Několik řešených příkladů | 2.4 A na konec ještě pár příkladů k procvičení |

Časové řady I |

Výstupy z výukové jednotky | 1 Vzorkování |

1.1 Seznamme se | 1.2 Vzorkovací teorém |

2 Základní typy matematických modelů veličin diskrétních v čase |

2.1 Konvence na začátek | 2.2 Periodické posloupnosti | 2.3 Jednorázové posloupnosti |

3 Základní operace s matematickými modely veličin diskrétních v čase |

3.1 Úvodní poznámky | 3.2 Diskrétní konvoluce | 3.3 Diskrétní korelační posloupnost |

Časové řady II |

Matematický popis systémů pracujících ve spojitém čase I |

Výstupy z výukové jednotky | 1 Linearita | 2 Vnější (vstupní/výstupní) popis lineárních systémů |

2.1 Lineární diferenciální rovnice |

3 Laplacova transformace |

3.1 Zavedení Laplacovy transformace | 3.2 Důležité vlastnosti Laplacovy transformace |

4 Vnější (vstupní/výstupní) popis - pokračování |

4.1 Obrazová přenosová funkce | 4.2 Rozložení nulových bodů a pólů operátorové přenosové funkce | 4.3 Frekvenční přenosová funkce a frekvenční charakteristiky | 4.4 Impulzní charakteristika | 4.5 Přechodová charakteristika | 4.6 Vzájemné vztahy mezi různými formami vnějšího popisu lineárního systému |

Matematický popis systémů pracujících ve spojitém čase II |

Výstupy z výukové jednotky | 1 Vnější popis nelineárních systémů | 2 Vnitřní (stavový) popis |

2.1 Lineární případ | 2.2 Nelineární případ |

3 Chování systémů |

3.1 Základní jevy v systémech |

4 Stabilita |

4.1 Základní pojmy | 4.2 Zkoumání stability | 4.3 Zobecněná stabilita dle Ljapunova |

5 Kauzalita |

Matematický popis lineárních systémů pracujících v diskrétním čase |

Výstupy z výukové jednotky | 1 Vnější (vstupní/výstupní) popis |

1.1 Diferenční rovnice |

2 Transformace Z |

2.1 Zavedení transformace Z | 2.2 Důležité vlastnosti transformace Z |

3 Vnější (vstupní/výstupní) popis - pokračování |

3.1 Obrazová přenosová funkce | 3.2 Rozložení nulových bodů a pólů obrazové přenosové funkce | 3.3 Frekvenční přenosová funkce a frekvenční charakteristiky | 3.4 Časové charakteristiky |

4. Vnitřní (stavový) popis | 5 Stabilita |

Systémové struktury |

4.3 Princip zpětnovazební regulace | 4.1 Popis přenosu zpětnovazebního systému | 4.2 Vlastnosti zpětnovazebního zapojení |

Komplexní čísla |

Výstupy z výukové jednotky | Základní typy popisu komplexních čísel | Matematické operace s komplexními čísly | Komplexní exponenciála |

Spojité deterministické modely I | Diskrétní deterministické modely | Úvod do matematického modelování | Vybrané kapitoly z matematického modelování |

2 Základní unární operace s funkcemi se spojitým časem

Násobení konstantou

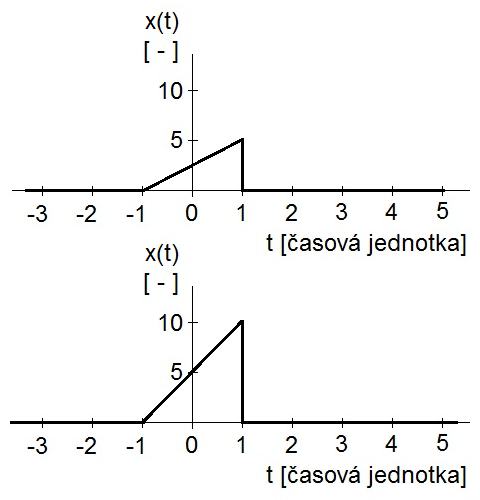
Okamžitá hodnota funkce se zvětší (zmenší) -krát po násobení funkce konstantou. Pro hovoříme o zesílení, pro o zeslabení, resp. útlumu (obr. Modely veličin spojitých v čase I 12).

Obr. 12. Násobení konstantou – A=2

Změna časového měřítka

Po vynásobení hodnot nezávisle proměnné (času) konstantou k dochází k modifikaci časového měřítka – pro hovoříme o časové kompresi, pro o časové expanzi.

Je třeba si uvědomit, že po změně měřítka nabývá funkce v čase t týchž hodnot jako původní funkce v čase pro tedy plyne čas rychleji, pro plyne čas pomaleji (obr. Modely veličin spojitých v čase I 13).

Posunutí v čase

Po přičtení (odečtení) hodnoty od původního času dochází k posunu časového průběhu funkce vlevo (vpravo) na časové ose. Jinými slovy po přičtení hodnoty dochází ke zpoždění funkce, po odečtení se funkce předchází (obr. Modely veličin spojitých v čase I 14).

V čase posunutá funkce nabývá v čase hodnot, kterých nabývá původní funkce v čase Kterým směrem dochází k posunu si lze nejsnáze uvědomit pro čas Aby posunutá funkce nabyla téže hodnoty jako původní v čase pak musí být argument též roven nule. Tedy, přičítáme-li je argument nulový pro odečítáme-li je argument nulový pro


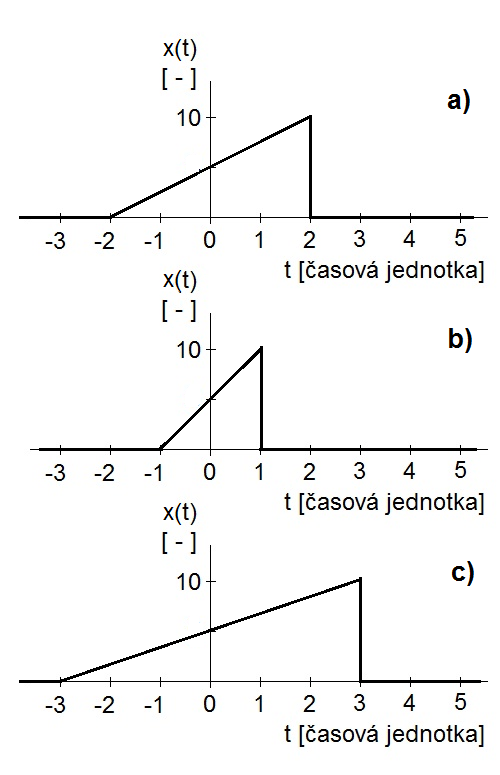
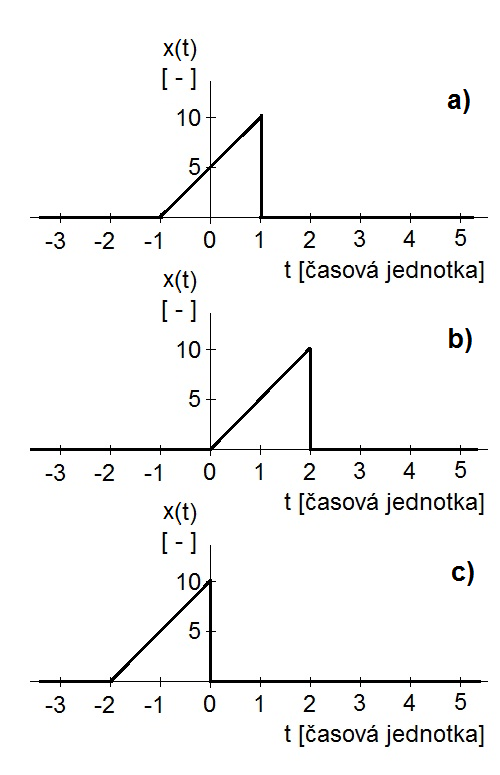
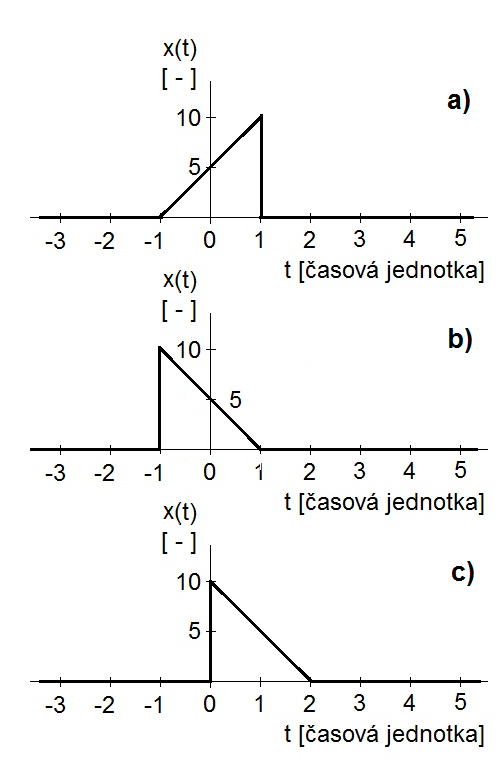
*Obr. 13.* Změna časového měřítka - a) originál; b) k=2; c) k=2/3	*Obr. 14.* Posunutí v čase - a) originál x(t); b) funkce x(t-1); c) funkce x(t+1);	*Obr. 15.* Inverze časové osy - a) originál x(t); b) funkce x(-t); c) funkce x(-t+1)

Inverze časové osy

Inverzi časové osy provedeme změnou znaménka časového argumentu. Má-li současně dojít k časovému posunu, je třeba změnit znaménko i u orientace časového posunu (obr. Modely veličin spojitých v čase I 15).

Příklad 2.1. Průběh funkce zobrazené na obr. Modely veličin spojitých v čase I 15 je definován vztahy

To znamená. že pro vybrané hodnoty nezávisle proměnné nabývá funkce funkčních hodnot dle následující tabulky (i tak jak to odpovídá průběhu na obr. Modely veličin spojitých v čase I 15a):

-2

-1

0

1

2

0

0

5

10

0

Pro vybrané hodnoty nezávisle proměnné nabývá v čase invertovaná funkce následujících hodnot (obr. Modely veličin spojitých v čase I 15b):

-2

-1

0

1

2

2

1

0

-1

-2

0

10

5

0

0

Konečně, pro argument a zvolené hodnoty proměnné nabývá posunutá a v čase invertovaná funkce následující funkční hodnoty (obr. Modely veličin spojitých v čase I 15c):

-2

-1

0

1

2

3

2

1

0

-1

0

0

10

5

0

Příklad 2.2. Jak lze zapsat funkci definovanou vztahem Modely veličin spojitých v čase I (31) tak, aby její velikost byla počátek nárůstu byl v bodě a konec lineárního nárůstu v bodě ?

Řešení

¹unární operace je taková operace, která má jediný operand

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity