4.3 Frekvenční přenosová funkce a frekvenční charakteristiky

Jak jsme již dříve uvedli, Laplacova proměnná má obecně komplexní charakter a můžeme ji také psát ve tvaru kde je koeficient tlumení a je kruhová (úhlová) frekvence harmonické funkce. Jak bylo uvedeno výše v kapitole o Laplacově transformaci, funkce resp. má obecně tvar tlumeného, resp. zesilovaného harmonického průběhu.

Předpokládejme nyní, že koeficient tlumení Pak po dosazení za v operátorové přenosové funkci dostáváme

(37)

Tuto funkci nazýváme frekvenční přenosovou funkcí lineárního systému. Protože opět jde o způsob vnějšího popisu vlastností lineární soustavy, vyjadřuje vztah mezi vstupní a výstupní funkcí soustavy, resp. lépe mezi harmonickými složkami, ze kterých se obě funkce skládají. Modul frekvenční přenosové funkce říká, jaký je vztah mezi amplitudami harmonických složek dané frekvence, ze kterých jsou vstupní i výstupní funkce složeny, argument frekvenční přenosové funkce definuje, jaký je fázový (resp. časový) posun mezi harmonickými složkami vstupu a výstupu.

obrazová přenosová funkce
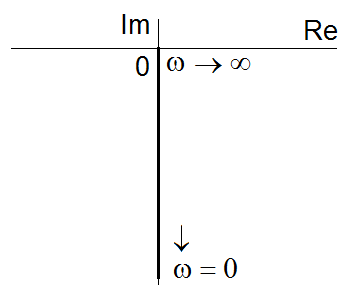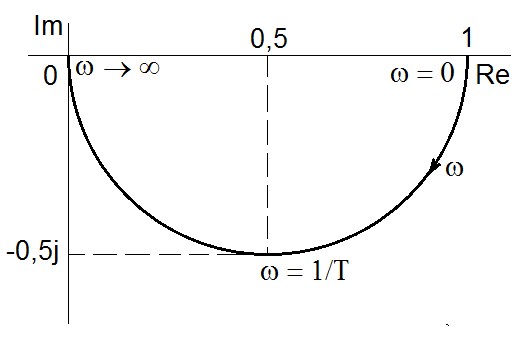
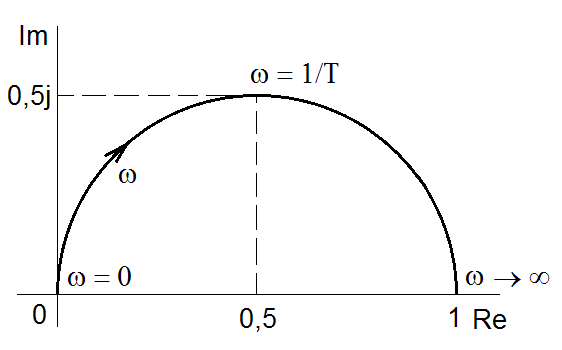
Obr. 4. Příklady frekvenčních charakteristik v komplexní rovině pro vybrané typy jednoduchých operátorových přenosových funkcí

Z frekvenční přenosové funkce odvozujeme frekvenční charakteristiky systému. Frekvenční charakteristika je především grafické vyjádření frekvenční přenosové funkce systému – je to geometrické místo koncových bodů vektorů přenosu pro frekvence v intervalu

Frekvenční charakteristiky vyjadřujeme zpravidla dvěma způsoby:

1. frekvenční charakteristika v komplexní rovině;
2. modulová a fázová charakteristika.

ad a.

V tomto případě kreslíme frekvenční charakteristiku v komplexní rovině, do které vynášíme hodnoty frekvenčního přenosu pro úhlovou frekvenci jako parametr; frekvenční vlastnosti systému vyjadřuje křivka v komplexní rovině, jejímž parametrem je kruhová frekvence (obr. Matematický popis systémů pracujících ve spojitém čase I 4 pravý sloupec).

ad b.

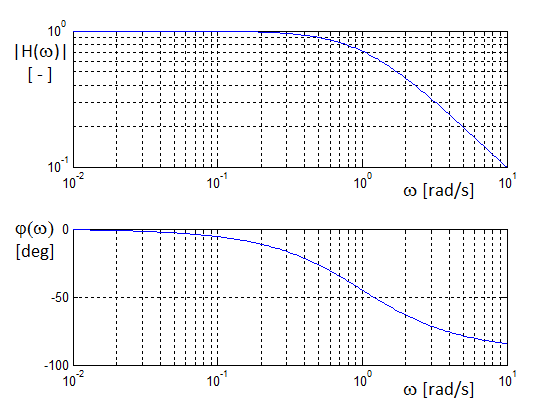
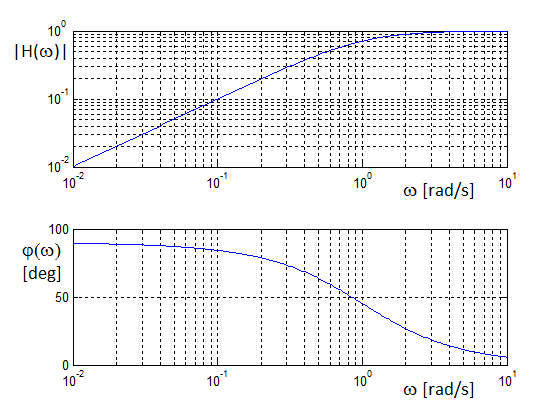
Frekvenční vlastnosti systému určují dvě funkce - závislost modulu frekvenčního přenosu na frekvenci a závislost fáze frekvenčního přenosu na frekvenci (obr. Matematický popis systémů pracujících ve spojitém čase I 5).

a)	b)
Obr. 5. Modulová a fázová frekvenční charakteristika (s použitím logaritmického měřítka) systémů s operátorovou přenosovou funkcí – a) H(p) = 1/(p+1); b) H(p) = p/(p+1), tj. charakteristiky pro systémy s přenosovými funkcemi podle obr. Matematický popis systémů pracujících ve spojitém čase I 4 s T = 1.

(38)

Velice praktickým nástrojem, jak získat orientační představu o tvaru modulové a frekvenční charakteristiky lineární soustavy jsou tzv. Bodeho charakteristiky

Příklad 4.5. Ukažte, že frekvenční charakteristika v komplexní rovině systému s přenosovou funkcí  má tvar polokružnice o poloměru 0,5 a středem v bodě jak je zobrazeno na obr. Matematický popis systémů pracujících ve spojitém čase I 4.

Řešení. Získejme nejprve orientační představu, kterými body frekvenční charakteristika prochází. Po dosazení za je  Nyní určeme body komplexní roviny, kterými charakteristika prochází, tj. určíme hodnoty pro a

1. pro je

2. pro je

3. pro je

což jsou všechno body zobrazené na obr. Matematický popis systémů pracujících ve spojitém čase I 4.

Nyní musíme ukázat, že funkce  je rovnicí kružnice v komplexní rovině s uvedenými parametry. Tedy předpokládejme, že tomu tak je. V tom případě musí platit

přičemž  a Dosadíme-li za a do levé strany předcházející rovnice, dostáváme po úpravách

což je právě pravá strana vztahu, který jsme chtěli dokázat.