2.1 Lineární případ

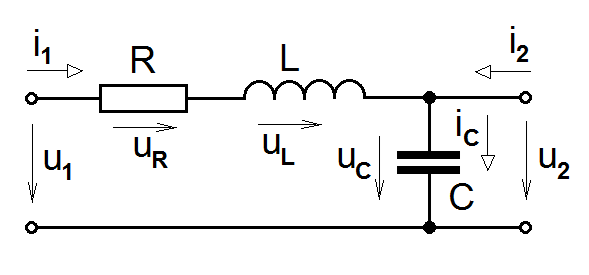
Pojďme se vrátit ke stále opakovaně používanému pasivnímu lineárnímu elektrickému modelu cévního segmentu, jak je zde znovu ukázán na obr. Matematický popis systémů pracujících ve spojitém čase II 2.

Obr. 2. Pasivní sériový RLC obvod jako elektrický model cévního segmentu

Nyní použijme veličiny, které popisují integrační (akumulační) charakter obou prvků, tj. napětí na kondenzátoru a proud cívkou, k popisu dějů uvnitř obvodu (stavového popisu).

Z definice napětí na kondenzátoru je

(10)

a z rovnice

(11)

dostáváme po normalizaci a separaci derivace proudu

(12)

Vytvoříme-li vektor veličin a jejich derivací pak můžeme zapsat obě výše uvedené rovnice v maticové tvaru

(13)

Vektor nazýváme stavový vektor systému.

Obecně lze výše uvedenou rovnici zapsat jako soustavu n diferenciálních rovnic 1. řádu (n je počet stavových akumulačních proměnných, n je i řád systému) jako

(14)

kde je stavový vektor (vektor stavových veličin), matice je matice dynamiky systému (matice vnitřních vazeb, matice zpětných vazeb, matice systému) a matice je matice vstupních vazeb systému (vstupní matice). Tento zápis definuje tzv. první stavovou rovnici systému. Druhá stavová rovnice definuje vztah mezi výstupními veličinami systému a jeho stavovými a vstupními veličinami. Tedy

(15)

kde je vektor výstupních veličin, matice je matice vazeb stavu systému na výstup (výstupní matice systému) a matice je matice přímých vstupně-výstupních vazeb.

Protože v úvodním příkladu je výstupní napětí definováno pomocí stavových a vstupních veličin jednoduchým vztahem

(16)

má druhá (výstupní) stavová rovnice zadaného elektrického obvodu tvar

(17)

Příklad 2.1. Určete vlastní (nebo též charakteristická) čísla matice dynamiky systému a srovnejte je s póly obrazové přenosové funkce téhož systému, tj. s kořeny charakteristické rovnice systému.

Řešení. Charakteristická rovnice určená pro dané zapojení v předchozí výukové jednotce příklad Matematický popis systémů pracujících ve spojitém čase I 4.1 z přenosové funkce je

Řešením této kvadratické rovnice pro proměnnou p získáme póly přenosové funkce.

Vlastní čísla matice získáme řešením rovnice kde představuje vlastní číslo matice a je jednotková matice. V našem konkrétním případě je matice dynamiky systému rovna

a tedy pro určení vlastních čísel řešme rovnici

To znamená, že

Srovnáním výše uvedené charakteristické rovnice a právě vypočítané rovnice pro určení vlastních čísel vidíme, že při ekvivalenci laplacovské proměnné a vlastních čísel jsou obě rovnice stejné. Řešením obou rovnic tudíž získáme tytéž hodnoty pólů přenosové funkce a vlastních čísel matice dynamiky systému a to

Tento konkrétní výsledek můžeme zobecnit do závěru, že analýza hodnot pólů obrazové přenosové funkce a vlastních čísel matice dynamiky systému v podstatě představuje totéž.