1 Diskrétní Fourierova řada

Rozklad spojitých veličin na harmonické složky jsme začali rozkladem periodických funkcí pomocí Fourierovy řady. Připomeňme dva základní vztahy pro Fourierovu řadu v exponenciálním tvaru pro spojité periodické funkce. Podle kterých spojitou veličinu lze rozložit na nekonečný součet dílčích harmonických složek, jejichž frekvence jsou celočíselnými násobky základní úhlové frekvence podle

kde  jsou komplexní Fourierovy koeficienty definované vztahem

a je opět úhlový kmitočet základní harmonické složky určený základní periodou rozkládané funkce Modul komplexního Fourierova koeficientu  určuje amplitudu odpovídající harmonické složky, jeho fáze hodnotu počáteční fáze odpovídající harmonické funkce.

Fourierova řada pro spojité funkce je definovaná nekonečným součtem harmonických složek. To vyplývá ze skutečnosti, že komplexní exponenciála se spojitým časem jako jádrová funkce harmonického rozkladu nabývá různých hodnot pro různé hodnoty úhlového kmitočtu Situace je ale zcela odlišná u diskrétní jádrové posloupnosti jejíž hodnoty se opakují s periodou kmitočtu protože je a perioda časové řady je dána počtem jejích vzorků, tj. V tom případě je

(1)

a pokud index udávající pořadí frekvenční složky, je větší než počet vzorků v periodě časové řady, pak se hodnoty komplexní jádrové exponenciály opakují.

Chceme-li najít diskrétní ekvivalent Fourierovy řady pro spojité funkce, pak musíme vzít v potaz tuto skutečnost a počet frekvenčních složek ve spektru diskrétní posloupnosti již nebude nekonečný, nýbrž omezený vzorkovací frekvencí na vzorků.

Protože je diskrétní Fourierova řada reprezentována konečným součtem dílčích složek, nejsou problémy, na rozdíl od případu se spojitým časem, s její konvergencí.

Definice 1.1. Nechť tedy je periodická posloupnost s periodou Tu lze rozložit pomocí komplexní exponenciální Fourierovy řady pomocí vztahu

(2)

kde

(3)

Důkaz. Změňme index sumace ve vztahu pro výpočet koeficientu

(4)

Pak je

	(5)

Potom pro je

(6)

a pro pomocí vztahu pro součet geometrické posloupnosti je

(7)

a tedy (protože součet je nenulový pouze pro )

(8)

Tedy což bylo to, co jsme chtěli dokázat.

Příklad 1.2. Určete spektrum posloupnosti

Řešení. Nejdříve spočítejme úlohu spíše na základě logických úvah. Zadaná posloupnost je periodická s periodou a můžeme si ji vyjádřit pomocí Eulerova vztahu ve tvaru

Nyní protože

je

Z toho plyne, že

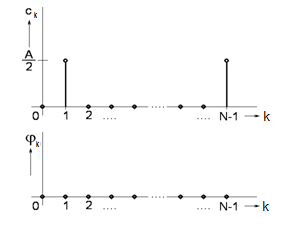
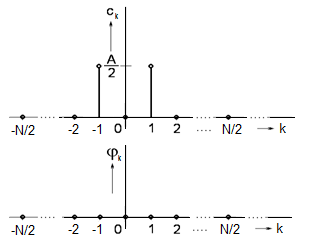
Spektrum tohoto signálu pak můžeme graficky vyjádřit s periodou a díky periodičnosti jádrové funkce řady i v periodě jak je tomu na obr. Časové řady II 1.

a)	b)
Obr. 1. Amplitudové a fázové spektrum posloupnosti x(nTvz) = A.cos(2pn/N) – a) s periodou <0,N-1>; b) s periodou <-N/2,N/2>

Pokusme se nyní spočítat koeficienty diskrétní Fourierovy řady pro danou posloupnost podle definičního vztahu. Nejdříve stejnosměrnou složku, tj. pro Podle Časové řady II (3) je

Protože součet vzorků kosinové posloupnosti přes jednu celou periodu je nulový, je hodnota  rovněž nulová (pro stejnosměrnou složku určitě dle očekávání).

Nyní určeme hodnotu Fourierova koeficientu pro

Součet v prvním členu je druhý součet, stejně jako třetí i čtvrtý jsou nulové (druhý a čtvrtý, protože se týká součtu vzorků kosinusovky, resp. sinusovky přes dvě celé periody – sice přes vzorků, ale obě harmonické funkce mají dvojnásobnou frekvenci než je zadaná, třetí součet je snad hanba vysvětlovat). Takže výsledná hodnota je

tak jak v úvodní fázi řešení. Výpočet pro a pro všechny ostatní je už ekvivalentní.