1 Vnější popis nelineárních systémů

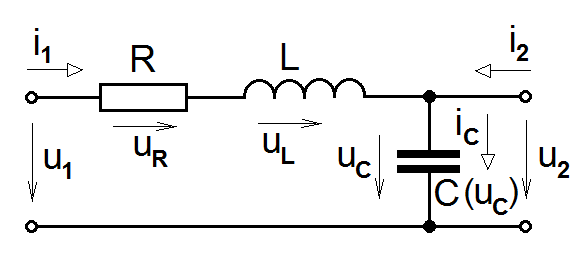
Nyní předpokládejme model cévního segmentu s reálnou modifikací, kdy je roztažnost cévní stěny závislá na tlaku krve v cévě. V základním náhradním elektrickém schématu to znamená jedinou změnu - předpokládáme kapacitu kondenzátoru (objem cévy) závislou na napětí na kondenzátoru (tlaku krve v cévě) (obr. Matematický popis systémů pracujících ve spojitém čase II 1). To znamená, že do systému zavedeme jednu nelinearitu.

Obr. 1. Náhradní nelineární elektrické schéma cévního segmentu

Odvození diferenciální rovnice uvedené v předchozí výukové jednotce v kap. 2.1 Lineární diferenciální rovnice za této podmínky dospěje beze změny až k rovnici Matematický popis systémů pracujících ve spojitém čase I (8) – uveďme ji zde ještě jednou a označme (8’)

(8')

a zde se bohužel vyskytne komplikace při určování proudu obvodem, protože vztah pro okamžité napětí na kondenzátoru se mění na

(1)

Z toho plyne

(2)

a potom pro platí (pokud poněkud zjednodušíme zápis vynecháním časové závislosti, která ale samozřejmě nepřestává platit)

(3)

Protože do vztahu Matematický popis systémů pracujících ve spojitém čase II (8‘) potřebujeme znát jak vztah pro proud (průtok), tak i pro jeho derivaci, potřebujeme výraz v Matematický popis systémů pracujících ve spojitém čase II (3) ještě jednou derivovat. To bychom snad zvládli i obecně, situaci si ale trošku zjednodušme konkrétním předpokladem o lineární závislosti Výpočet to zjednoduší, závěry, kvůli kterým jej provádíme, to neovlivní. Pišme tedy

(4)

a pro derivaci

(5)

Dosadíme-li oba výrazy do Matematický popis systémů pracujících ve spojitém čase II (8‘), dostaneme

(6)

Přepíšeme-li diferenciální rovnici Matematický popis systémů pracujících ve spojitém čase II (6) do očekávaného tvaru, dostaneme

(7)

a z toho

(8)

kde

(9)

Získaná diferenciální rovnice zůstává 2. řádu (počet akumulačních prvků se přece nezměnil), ale zavedení nelineární závislosti kapacity na napětí kondenzátoru způsobilo, že všechny uvedené parametry diferenciální rovnice, tj. i jsou funkcemi výstupního napětí a diferenciální rovnice je tedy nelineární. Protože určená diferenciální rovnice sama definuje závislost výstupního napětí na vstupním, můžeme konstatovat, že parametry soustavy formálně závisejí i na jejím vstupu. Z toho konečně plyne ponaučení, které lze zobecnit, totiž že vlastnosti nelineární soustavy nezávisejí pouze na struktuře samotné soustavy, nýbrž i na jejím vstupu, což samozřejmě případnou analýzu významně komplikuje.

Nyní zkusme určit obrazovou přenosovou funkci nelineární varianty obvodu s diferenciální rovnicí, která je podle Matematický popis systémů pracujících ve spojitém čase II (7)

nebo v obecném tvaru podle Matematický popis systémů pracujících ve spojitém čase II (8)

Protože jednotlivé členy uvedené diferenciální rovnice jsou dány součiny funkce a derivace určité proměnné, lze její Laplacovu transformaci počítat (pokud vůbec) pouze pro daný konkrétní případ a nelze obecně stanovit tvar operátorové funkce nelineárního systému.

Tedy shrňme, nelineární soustavu lze popsat nelineární diferenciální rovnicí, obrazovou přenosovou funkci obecně sestavit nejde, a tudíž nemá smysl se zabývat ostatními způsoby popisu používanými pro popis lineárních soustav. Nelze se tedy zabývat ani frekvenčními vlastnostmi nelineárních soustav.