
4.3 Zobecněná stabilita dle Ljapunova
V příkladu v kap. 1 této výukové jednotky jsme si ukázali, že vlastnosti a chování nelineárního systému nezávisí jen na parametrech samotného systému, ale současně i na vlastnostech a charakteru vstupů. Proto v případě nelineárních systémů nelze vystačit se zjednodušeným přístupem ke stabilitě tak, jak jsme ho použili pro systémy lineární. Pojem stability je proto třeba poněkud zobecnit.
Nechť je systém popsán diferenciální rovnicí kde
je obecně nelineární funkce. Její řešení pro počáteční podmínku
označíme
a pro málo odlišnou počáteční podmínku
je
Pro stabilitu je podstatné jaký je rozdíl obou řešení, jestli se počáteční podmínky liší jen málo.
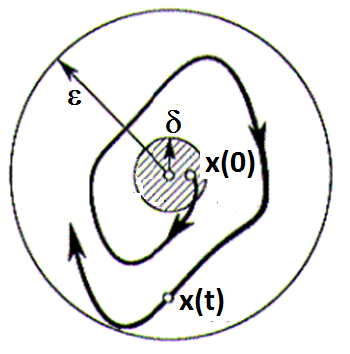
Abychom formalizovali požadavek na rozdíl obou řešení, lze formulovat požadavek na stabilitu systému tak, aby ke každému počátečnímu stavu z okolí ustáleného stavu existovalo
okolí tohoto bodu, ze kterého se stav systému v celém průběhu řešení nevzdálí.
Požadavek ustálení stavu systému na původní hodnotě je zde zaměněn za požadavek malých pohybů kolem rovnovážného stavu.
 |
|
Obr. 4. Princip definice ljapunovské1 stability
|
1 Alexandr Michajlovič Ljapunov (*1857, Jaroslavl, Rusko, +1918 vlastní rukou bezprostředně po smrti své ženy, Oděsa, Rusko nebo Ukrajina?, těžko říct kam v roce 1918 Oděsa patřila), ruský matematik, statistik a fyzik; nejdůležitější přínos z oblasti diferenciálních rovnic a dynamických systémů, zejména jejich stability. Dokázal dokázat centrální limitní větu za podstatně obecnějších podmínek než jeho předchůdci.




