
Metoda vlastních vektorů
Systém rovnic Lineární rovnice (7) můžeme řešit také pomocí převedení matice na Jordanův kanonický tvar. Připomeňme, že matici
lze převést na Jordanovu matici
, což je matice nul, která má na diagonále tzv. Jordanovy buňky (submatice s vlastními čísly na diagonále, případně jedničkami nad ní, viz učivo lineární algebry). Pro převod matice na Jordanův tvar se používá regulární matice
, pro kterou platí
V případě různých vlastních čísel je zřejmé, že sloupce matice jsou postupně všechny (nezávislé) vlastní vektory příslušné všem vlastním hodnotám. V případě
-násobných vlastních hodnot (jde o algebraickou násobnost vlastního čísla
) se používá tzv. zobecněných vlastních vektorů
pro které platí
Substituce převádí rovnici Lineární rovnice (7) na rovnici
jejíž řešení lze nalézt "zespodu" elementárními metodami.
Příklad 4.1. Řešme rovnici Lineární rovnice (7) s maticí
se dvěma reálnými různými vlastními čísly
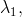
Vlastní vektory tedy splňují
a
Substituce
převádí úlohu na dvě elementární rovnice
které mají obecné řešení
Platí tedy
odtud
což je v naprostém souladu s (i) odstavce v časti Obecné řešení.
Příklad 4.2. Řešme rovnici Lineárné rovnice (7) s maticí 2x2 se dvěma reálnými vlastními čísly
algebraické násobnosti 2. Vlastní vektor příslušný
splňuje
a zobecněný vlastní vektor splňuje
Substituce
převádí úlohu na dvě elementární rovnice
jejichž obecné řešení lze odspodu vypočítat:
a
pak splňuje
Metodou variace konstanty dostáváme řešení ve tvaru
kde
Odtud
Platí tedy
odtud
což je v naprostém souladu s (ii) odstavce v částí Obecné řešení.
Příklad 4.3. Řešme rovnici Lineární rovnice (7) s maticí 2x2 se dvěma komplexně sdruženými vlastními čísly
Vlastní vektory jsou také komplexně sdružené, tj.
Substituce
převádí úlohu na dvě rovnice
jejichž řešení jsou v komplexním oboru:
a
Platí tedy
odtud
což je v naprostém souladu s (iii) odstavce Obecné řešení. Pokud navíc rozepíšeme vektor
na reálnou a imaginární složku, dostáváme
kde

jsou obecně komplexní konstanty, volbou reálných

tak dostáváme všechny reálné lineární kombinace dvou reálných řešení ve tvaru




