Evoluční hry a model jestřáb-holubice

V evoluční hře budou hráči geny, které řídí chování organismu. Strategií je fenotyp chování (fenotypem se rozumí soubor pozorovatelných vlastností a znaků), tedy geny předprogramované chování. Výplatní funkcí je fitness (biologická, reprodukční zdatnost), schopnost zachovat gen a rozšířit ho v genotypu populace (genotypem rozumíme soubor všech genů, které má organismus k dispozici). Strategie jedince daného fenotypu  spolu s danou výplatní maticí určuje při setkání s jedincem fenotypu fitness, zdatnost

Můžeme si ji představit např. jako výhru ve formě kvantifikace množství potravy přenechané zdatnějšímu jedinci nebo výhodnosti prostředí pro vyvedení mláďat apod.

Definice 2.1. O populaci fenotypu řekneme, že je evolučně stabilní vůči fenotypu pokud jsou jedinci fenotypu při vstupu malého počtu mutantního fenotypu zdatnější, tedy mají vyšší fitness. Formálně zapsáno tedy

nebo

pro libolné dostatečně malé (odtud vyplývá také nutná podmínka ).

Evolučně stabilní strategií  v daném prostoru strategií rozumíme strategii takovou,  že pro každou strategii a všechna dostatečně malá platí

Úpravou dostáváme

(3)

Věta 2.2. Smíšená strategie  je evolučně stabilní strategií právě tehdy, když je  rovnovážnou strategií, tj.

a platí

pro  které splňuje

Důkaz je zřejmý přímo z Evoluční dynamika a vývoj vzorců chování (3) v definici Evoluční dynamika a vývoj vzorců chování 2.1 a z poznámky Evoluční dynamika a vývoj vzorců chování 1.7. První podmínka říká, že strategie je Nashovou rovnováhou, je tedy nejlepší odpovědí sama na sebe. Druhá podmínka říká, že pokud existuje alternativní strategie se stejnou výplatou, je výhodnější odpovědí než na strategii

Klasická darwinistická a neodarwinistická teorie evoluce předpokládá, že kritériem evolučního úspěchu jedince je jeho fitness. Podle klasických představ by se v důsledku přirozeného výběru měli v populaci zachovat ty geny, které svému nositeli poskytují největší fitness. S nástupem evoluční teorie her se však ukázalo, že z dlouhodobého hlediska není důležité, jak příslušný gen mění fitness nositele, ale to, jestli podmiňuje evolučně stabilní strategii, tj. takovou strategii, která pokud jednou v populaci převládne, nemůže být potlačena žádnou jinou minoritní strategií. V evoluci tedy nevyhrává vždy zdatnější, jak si představoval Charles Darwin, ale stabilnější. Je potřeba si uvědomit, že mluvíme o selekci fenotypu, nikoliv o jeho mutaci. V případě vstupu nového fenotypu jde totiž o změnu prostoru strategií

Příklad. Uvažujme dvě populace jednoho druhu a bojující mezi sebou o zdroj potravy. představuje fenotyp chování hawk - jestřáb, který bojuje tvrdě, chladnokrevně a vzdává se jen tehdy, když je vážně zraněný, dove  - hrdlička se uchyluje jen k symbolické hrozbě a při přímém útoku utíká nezraněná. Cílem evoluční teorie her je určit zastoupení těchto dvou strategií v populaci a která z nich převládne. Výplatní matice této hry je dána následující tabulkou

kde  je představuje zisk (potravu), zatímco jsou náklady (ztráta energie, zranění apod.) na boj s druhým jedincem. Fenotyp hrdličky D se bez boje vzdává potravy fenotypu jestřába H, výplata je tedy nula. S hrdličkou se hrdlička o potravu rozdělí, výplata je Jestřáb o potravu buď bojuje s jestřábem a získá polovinu potravy zmenšené o náklady na boj nebo ji získá od hrdličky v celé výši

Uvažujme nejprve populaci fenotypu Vstoupí-li do ní jedinec fenotypu bude se v ní s jistotou šířit, protože fitness - výplatní funkce tedy není evolučně stabilní strategie, protože není odolná vůči vstupu mutantního fenotypu.

Uvažujme naopak populaci fenotypu Vstoupí-li do ní jedinec fenotypu bude pro fitness platit

a logicky bude záviset na tom, zda zisk z boje bude větší nebo menší než náklady na boj V případě, že pak a mutantní fenotyp se v populaci nebude moci šířit. V této situaci bude fenotyp jestřába evolučně stabilní strategií. V opačném případě, kdy náklady převýší zisk bude se fenotyp hrdličky moci šířit v populaci jestřábů.

Uvažujme nyní případ, kdy tj. nemáme ryzí evolučně stabilní strategii. Uvažujme smíšenou strategii kdy se jedinec chová jako jestřáb s pravděpodobností a jako hrdlička s pravděpodobností pak fitness jednotlivých fenotypů je daná vztahy

Zapsáno pomocí formalismu smíšených strategií u symetrickým maticových her je tedy výplata hráče, který hraje strategii (fitness fenotypu H), při setkání s tímto jedincem hrajícím smíšenou strategii

Podobně

Přitom platí

Smíšená strategie bude rovnovážná, pokud bude platit

(4)

což je druhá podmínka ve větě Evoluční dynamika a vývoj vzorců chování 1.8, protože uvažujeme pouze případ kdy rovnováhou nemůže být ryzí strategie a tudíž V případě, že by tomu tak nebylo, fenotyp H by měl v populaci smíšené strategie vyšší (resp. nižší) fitness než fenotyp D v této populaci a bylo by výhodnější změnit poměr H a D, tj. hrát jinou smíšenou strategii. Protože

pokud

je (Ověřte, že platí celá podmínka Evoluční dynamika a vývoj vzorců chování (4)!) Navíc je zřejmé, že pokud dochází k šíření fenotypu v populaci smíšené strategie, tj. bude růst, naopak pokud dochází k šíření fenotypu poklesu To nám tedy zaručuje evoluční stabilitu této smíšené strategie

Pokud bychom chtěli pro důkaz ESS použít větu Evoluční dynamika a vývoj vzorců chování 2.2, pak podmínka rovnováhy říká, že

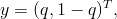
pro každé Tato podmínka je splněna, protože

Tím je zaručena rovnovážnost smíšené strategie  Druhá podmínka zaručuje ESS a tvrdí, že pokud nějaká strategie splňuje pak Podmínka je splněna pro všechny
Dosazením a úpravou vidíme, že

a tím je zaručena také evoluční stabilita smíšené strategie 

Úlohy k procvičení