Systémy diferenciálních rovnic a rovnice vyššího řádu
Vektorové a maticové funkce
Doposud jsme měli jednu tzv. stavovou proměnnou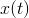 
, tj. proměnnou, jejíž stav se v čase mění. Reálné procesy ale většinou ovlivňuje více stavových proměnných. Můžeme si představit např. chemickou reakci dvou látek. Koncentrace těchto látek ovlivňují chemickou reakci a v průběhu reakce se mění. Jiným příkladem může být např. ekosystém živočišných nebo rostlinných druhů, jejichž populace se navzájem ovlivňují. Pro modelování složitějších reálných procesů tedy budeme potřebovat více stavových proměnných, použijeme proto nástroje lineární algebry a jejich rozšíření, např. vektorové a maticové funkce.
Reálný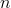 
-rozměrný vektor 
je prvkem prostoru 
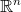. Složky (standardní souřadnice) vektoru budeme značit 
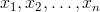nebo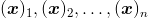 
.
Matice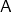 
o 
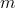řádcích a 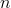sloupcích je prvkem prostoru 
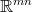. Její prvek na 
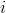-tém řádku a v 
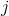-tém sloupci
budeme značit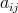 
nebo 
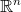. Vektor z prostoru budeme chápat jako matici o 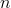řádcích a jednom sloupci.
Je-li tedy 
a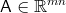 
, můžeme psát
Normy vektorů a matic
Normu vektoru
podrobněji vektorovou 1-normu nebo součtovou normu definujeme předpisem
Normu matice
podrobněji maticovou 1-normu nebo součtovou normu definujeme předpisem
Na množině vektorů zavádíme metriku 
, na množině matic zavádíme metriku
- Platí:
. Této vlastnosti se říká, že maticová norma je souhlasná s vektorovou normou.
Důkaz: Pro libovolné 
je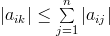 
. Odtud plyne
Spojitost, derivace a integrál vektorových a maticových funkcí
Vektorová funkce, podrobněji 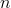-vektorová funkce, 
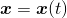je zobrazení 
, maticová funkce, podrobněji čtvercová
Na množině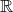 
uvažujeme běžnou metriku 
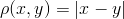, na množině 
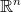, resp. 
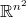, uvažujeme příslušnou součtovou metriku. Spojitost vektorové (resp. maticové) funkce chápeme jako spojitost příslušného zobrazení metrických prostorů. Podrobněji: vektorová funkce (resp. maticová funkce 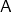) je spojitá v bodě 
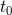svého definičního oboru, jestliže ke každému kladnému číslu 
existuje kladné číslo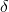 
tak, že pro všechna 
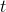z definičního oboru funkce z nerovnosti 
plyne nerovnost (resp. 
). Vektorová (resp. maticová) funkce je spojitá právě tehdy, když všechny
její složky jsou spojité.
Limitu v bodě 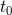, derivaci v obecném bodě 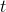a integrál v mezích od 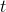do 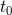vektorové, resp. maticové, funkce definujeme vztahy (v uvedeném pořadí)
Definice systémů ODR a ODR vyšších řádů
Nyní tedy máme k dispozici aparát a v následujícím textu s jeho pomocí rozšíříme pojmy uvedené v části Obyčejná diferenciální rovnice prvního řádu pro více stavových proměnných.
Definice 3.1. Buď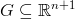 
množina s neprázdným vnitřkem, 
. Rovnice
se nazývá systém 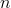obyčejných diferenciálních rovnic prvního řádu nebo 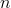-vektorová obyčejná diferenciální
rovnice prvního řádu.
Vektorovou rovnici můžeme rozepsat do složek
Počáteční podmínku k rovnici Obyčejné diferenciální rovnice (4) zadáváme ve tvaru
Pojmy řešení, obecné řešení, partikulární řešení, úplné řešení rovnice Obyčejné diferenciální rovnice (4) jsou analogiemi těchto pojmů z jednorozměrného případu. Obecné řešení závisí na 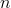parametrech.
Příklad: Vraťme se nyní znovu k našim bylinkám. Napadly je mšice a my jsme je postříkali chemickým postřikem. Chemikálie se poté, co zahubí mšice, deštěm a zaléváním vsákne do půdy a bude vstřebávána bylinkami. Označme biomasu bylin, množství chemikálie v rostlině
a množství chemikálie v půdě
. Chemikálie přechází z půdy do biomasy, mění se tak koncentrace chemikálie v půdě i v bylinkách. Bylinky pravidelně ořezáváme. Modelem může být pak následující systém diferenciálních rovnic:
Pokusme se vysvětlit, co znamenají jednotlivé členy na pravé staně systému. První dva členy již známe - bylinky rostou a my je ořezáváme. Členy sa
odpovídají koncentraci chemikálie vynásobené množstvím biomasy. Bylinky
rostou tím pomaleji, čím větší je tato koncentrace
resp.
. Pokud je příliš velká, budou i hynout. Chemikálie přechází z půdy do rostliny. Můžeme říct, že čím více je chemikálie a čím více je biomasy, tím více ji rostlina z půdy získává. Je to velmi zjednodušený model, který vede na uvedený systém rovnic.
Úkol: Pokuste se systém upravit tak, aby chemikálie přecházela z půdy do rostliny také v závislosti na rychlosti růstu rostliny.
Definice 3.2. Buď 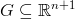množina s neprázdným vnitřkem, 
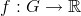. Rovnice
se nazývá obyčejná diferenciální rovnice 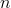-tého řádu rozřešená vzhledem k nejvyšší derivaci.
Řešením této rovnice se rozumí 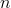-krát diferencovatelná funkce 
, kde 
je interval, která splňuje podmínky
pro každé 
Počáteční (Cauchyovu) podmínku pro rovnici Obyčejné diferenciální rovnice (5) zadáváme ve tvaru
kde 
.
Úplné řešení, obecné řešení, partikulární řešení rovnice Obyčejné diferenciální rovnice (5) definujeme analogicky jako u rovnic prvního řádu.
Obecné řešení závisí na 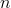parametrech.
Poznámka 3.3. Řešení počáteční úlohy Obyčejné diferenciální rovnice (5), Obyčejné diferenciální rovnice (6) je ekvivalentní s řešením počátečního problému pro systém 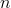diferenciálních rovnic prvního řádu:
|
|
(9) |
v tomto smyslu: Je-li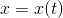 
řešením úlohy Obyčejné diferenciální rovnice (5), Obyčejné diferenciální rovnice (6), pak 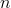-tice funkcí
je řešením úlohy Obyčejné diferenciální rovnice (7), Obyčejné diferenciální rovnice (8) a je-li 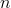-tice funkcí
řešením úlohy Obyčejné diferenciální rovnice (7), Obyčejné diferenciální rovnice (8), pak je funkce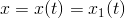 
řešením úlohy Obyčejné diferenciální rovnice (5), Obyčejné diferenciální rovnice (6).
Příklad: Rovnicese nazývá rovnice harmonického oscilátoru. Popisuje pohyb (výchylku z rovnováhy) tělesa jednotkové hmotnosti na pružině s koeficientem tuhosti
. Zrychlení musí odpovídat síle pružiny, která je tím větší, čím větší výchylku těleso má od rovnovážné polohy. Zanedbáváme samozřejmě tření i gravitační sílu. Rovnici můžeme přepsat na systém diferenciálních rovnic prvního řádu novým označením proměnných:
je výchylka tělesa,
je rychlost tělesa (opačné znaménko znamená opačný směr). Platí tedy:
Ukažte, že funkce, pro
jsou řešením rovnice harmonického oscilátoru. Jak vypadá řešení příslušného systému diferenciálních rovnic?
