Původní Hodgkinův-Huxleyho model popisuje dynamiku napětí na membráně pomocí nelineárních vztahů. Dalšími třemi stavovými proměnnými jsou míry aktivity iontových kanálů pro jednotlivé ionty. R. FitzHugh model zjednodušil jednak redukcí proměnných (odezvu iontových kanálů popsal jedinou lineární rovnicí) a také použil místo složitějších nelineárních funkcí nejjednodušší nelineární funkci zachovávající vlastnost podstatnou pro model - esovité prohnutí, tedy kubickou parabolu. Vzhledem k tomu, že jde o FS (Fast-Slow) systém, kde odezva je pomalou proměnnou oproti rychlé proměnné můžeme model zapsat rovnicemi

(1)

Zde tedy zastupuje rychlou proměnnou - membránové napětí, je velikost vstupujícího proudu (parametr), stavová proměnná nemá přímý biochemický význam, protože vznikla redukcí tří proměnných odpovídajících aktivitě jednotlivých iontových kanálů, představuje tedy jakousi obnovovací proměnnou, která má pomalejší odezvu a umožňuje vznik impulzu, který následně ukončí. Paramery splňují a parametr

Příklad. Analýza FitzHugova-Nagumova modelu Dynamika excitabilních systémů (1) pro
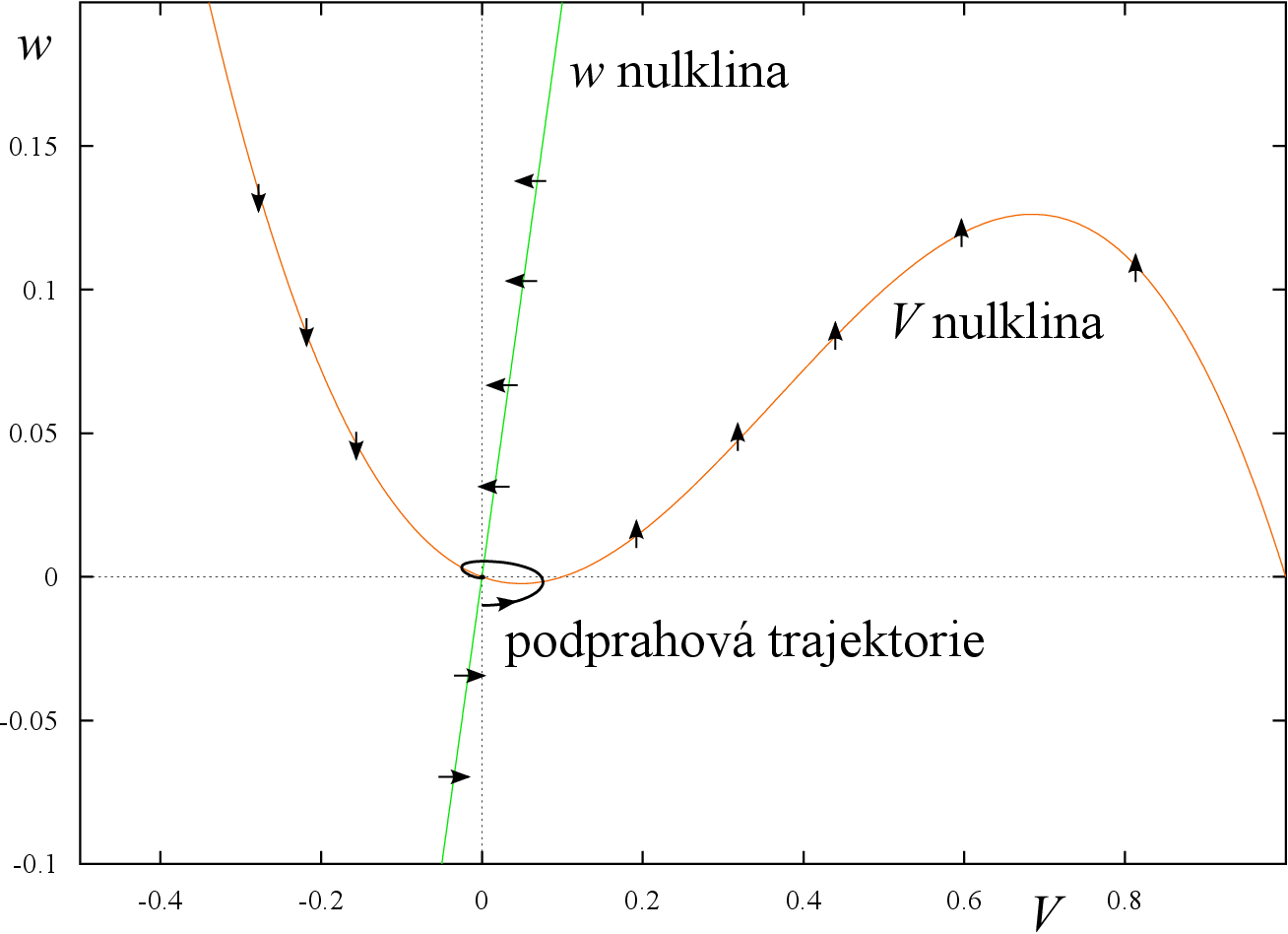
Nulkliny ve stavovém prostoru jsou kubická parabola procházející počátkem

a přímka procházející počátkem

(Nakreslete si nulkliny se směry procházejících trajektorií!) Počátek je tedy vždy rovnovážným bodem. Jeho stabilitu můžeme určit metodou linearizace. Jacobiho matice systému Dynamika excitabilních systémů (1) v počátku je

přitom stopa matice a determinant Podle tabulky Autonomní systémy a kvalitativní teorie 6.1 je rovnovážný bod stabilní. Další dvě rovnováhy by mohly vzniknout jako nenulové průsečíky kubické paraboly a přímky, musí tedy splňovat rovnici

Vzhledem k jde o kvadratickou rovnici, která má reálná řešení pouze pro

(2)

Typicky (pro neurony) se nulkliny protínají pouze jednou, protože hodnoty parametrů by mohly být např. a tj. podmínka Dynamika excitabilních systémů (2) není splněna.

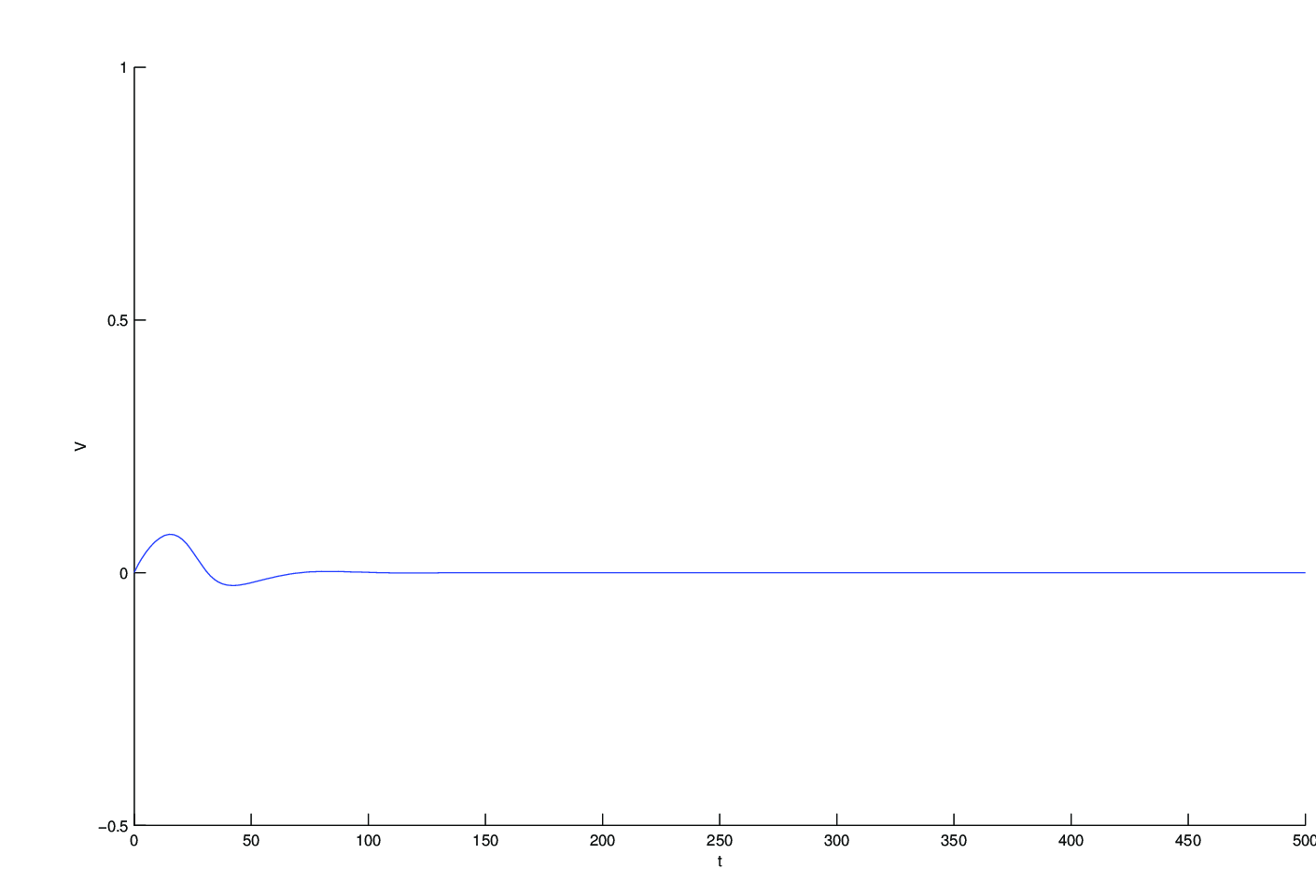
Pro názornost vykreslíme fázový portrét a řešení s počáteční podmínkou blízkou počátku pro tyto parametry. Jde o situaci, kdy neuron na malou změnu v aktivaci iontových kanálů nebo napětí nereaguje .

Obr. 1. Podprahová trajektorie systému Dynamika excitabilních systémů (1) ve stavovém prostoru.

Obr. 2. Podprahová trajektorie systému Dynamika excitabilních systémů (1), závislost potenciálu V membrány na čase.

Pokud dojde k dostatečně velké změně (depolarizace membrány, aktivace iontových kanálů), vzniká vzruch. Na obrázku Dynamika excitabilních systémů 3 to odpovídá snížení počáteční hodnoty stejně tak bychom mohli zvýšit počáteční hodnotu membránového potenciálu

Obr. 3. Nadprahová trajektorie systému Dynamika excitabilních systémů (1) ve stavovém prostoru.

Obr. 4. Nadprahová trajektorie systému Dynamika excitabilních systémů (1), závislost potenciálu V membrány na čase.

Zde jsme popsali princip vzniku vzruchu typu „vše nebo nic“. Chování excitabilních buněk je ale daleko složitější a pouze částečně je jej možné modelovat zjednodušeným modelem Richarda FitzHuga. Jev, který ale můžeme sledovat i u tohoto jednoduchého modelu je vznik periodicky se opakujících vzruchů.

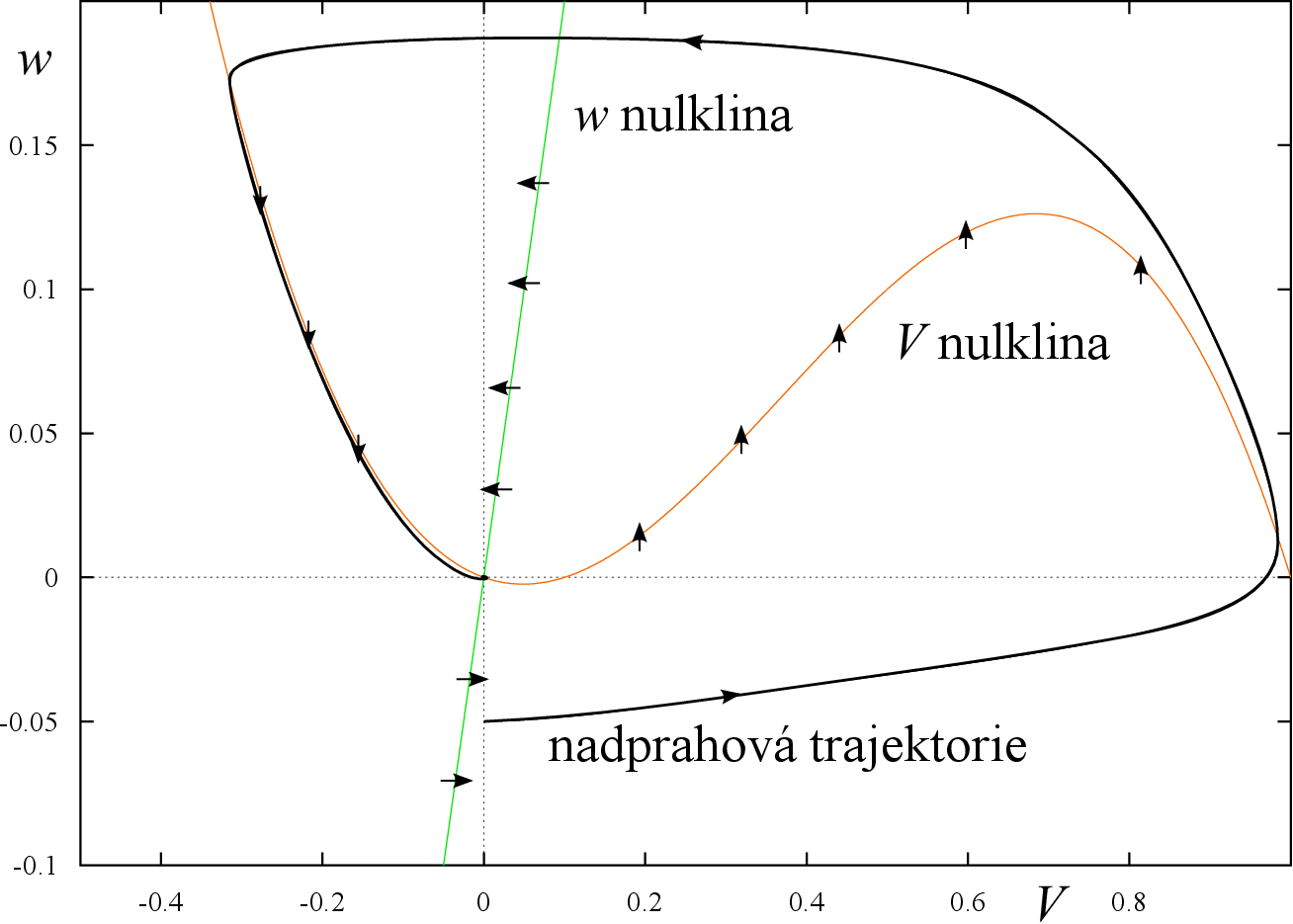
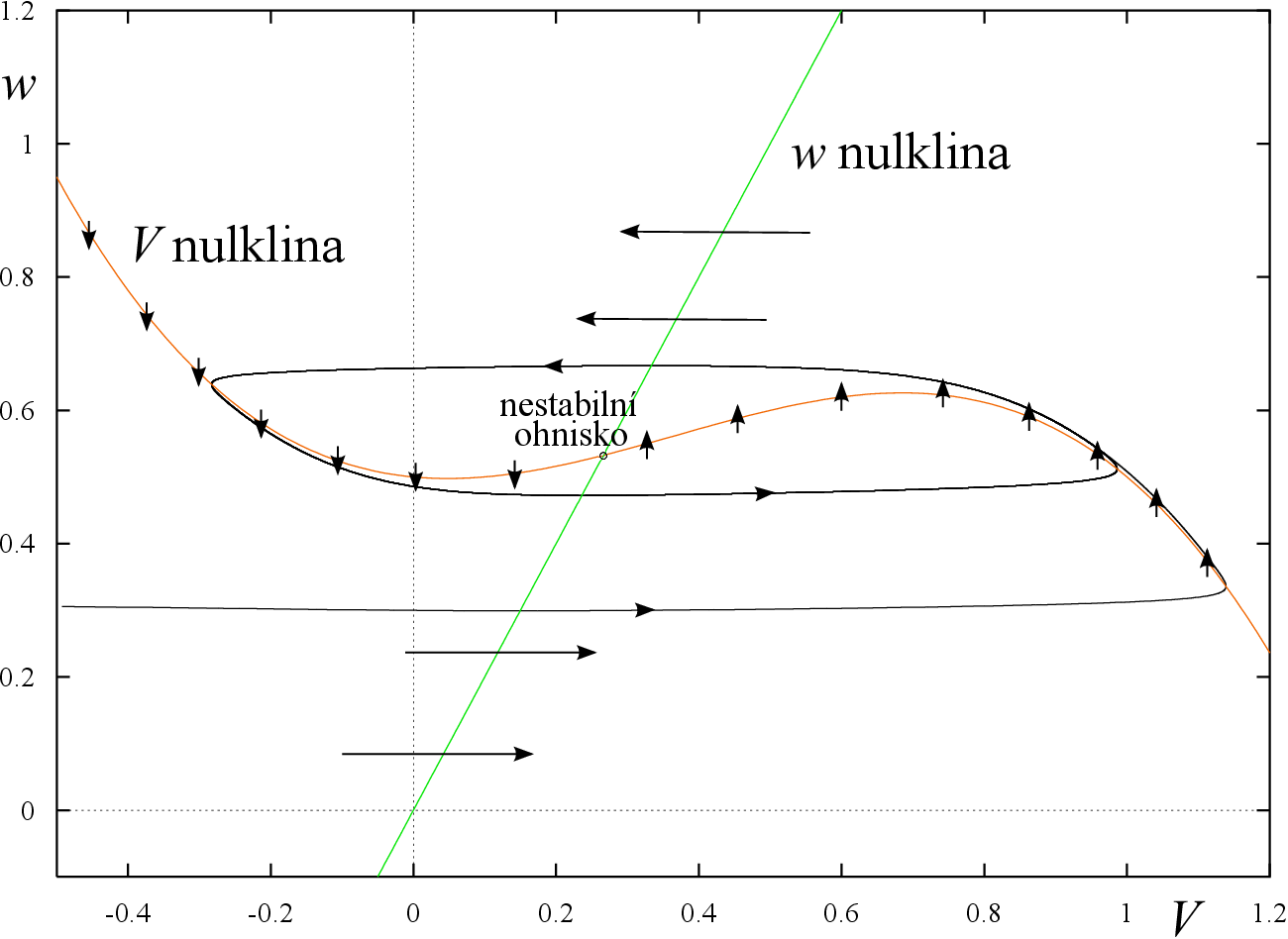
Předpokládejme, že membránu vystavíme elektrickému proudu Nulklina

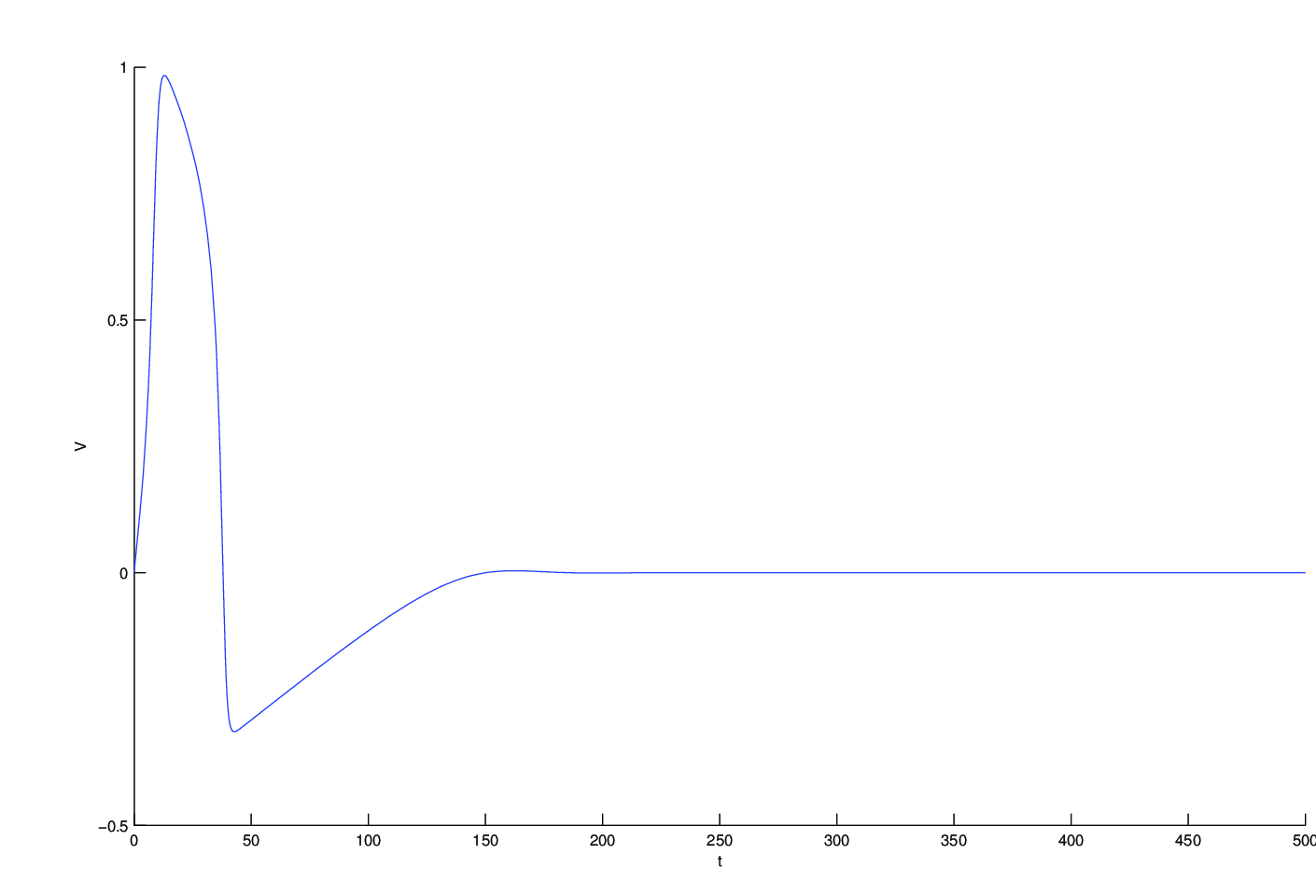
se zvedne a k průsečíku s nulklinou dojde pro kladnou hodnotu Navíc se změnou sklonu této nulkliny v tomto rovnovážném bodě dojde ke změně stability. Trajektorie z okolí počátku pak není přitahována k tomuto bodu. Pomocí Poincaré-Bendixsonovy věty pak lze ukázat, že uzávěr této trajektorie odpovídá oscilaci, limitnímu cyklu, který představuje periodické vzruchy.

Ukážeme si to pro konkrétně zvolené parametry a Rovnováhou pro tyto parametry je Jacobiho matice v tomto bodě je

a její vlastní čísla jsou a Rovnovážný bod je tedy nestabilní uzel.

Vzhledem k tomu, že proměnná je pomalá proměnná, všechny trajektorie dostatečně vzdálené od tohoto nestabilního uzlu jsou téměř rovnoběžné s osou dokud nenarazí na -nulklinu, v jejíž blízkosti začne převažovat změna pomalé proměnné - odezvy V okamžiku, kdy kubickou parabolu -nulkliny trajektorie opustí, bude mít tendenci kopírovat její tvar. V lokálním extrému tato možnost zmizí a trajektorie bude téměř rovnoběžně s osou (změna je pomalá) pokračovat až dokud se znovu nepřiblíží ke kubické nulklině. Takto vznikne stabilní limitní cyklus představující oscilace, periodické vzruchy.

Obr. 5. Oscilace, periodické vzruchy v systému Dynamika excitabilních systémů (1) s nenulovým vnějším proudem I.

Úlohy k procvičení

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity