Lineární rovnice
Lineární rovnice je rovnice typu
1. 
(homogenní rovnice)
Je to rovnice se separovanými proměnnými. Partikulární řešení počátečního problému (s podmínkou Obyčejné diferenciální rovnice (2)) je:
|
|
|
|
|
|
|
|
Obecné řešení homogenní lineární rovnice lze tedy zapsat
2. 
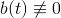(nehomogenní rovnice)
Řešení hledáme ve tvaru
(metoda variace konstanty). Pak
Dosazením do dané rovnice dostaneme
|
|
|
|
|
|
|
|
Obecné řešení nehomogenní rovnice tedy je
Partikulární řešení splňující počáteční podmínku Obyčejné diferenciální rovnice (2) je
Jsou-li koeficienty konstantní, 
, pak
Jiný postup při řešení nehomogenní rovnice:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Příklad: V předchozí kapitole jsme si uvedli příklad s pěstováním a sklizní bylinek, který vedl na lineární diferenciální rovnici Obyčejné diferenciální rovnice (3)Obecné řešení metodou variace konstanty hledáme nejprve pomocí nalezení obecného řešení homogenní lineární rovnice, tj.
. Partikulární řešení nehomogenní rovnice budeme tedy hledat ve tvaru
, přičemž dosazením do Obyčejné diferenciální rovnice (3) dostáváme
Obecným řešením nehomogenní rovnice je tedyPokud budeme hledat řešení Cauchyových úloh s počáteční podmínkouresp.
, musíme najít vhodnou hodnotu konstanty
, tj. pro podmínku
analogicky podmínkuTím dostáváme ona dvě partikulární řešení příslušných počátečních úloh
