Lineární a adaptivní zpracování dat |
Lineární a adaptivní zpracování dat: řešené úlohy v MATLABu |
Matematické modely v biologii |
Maticové populační modely |
Signály a lineární systémy |
Spojité deterministické modely I |
Obyčejné diferenciální rovnice |
Diskrétní deterministické modely |
Úvod do matematického modelování |
Vybrané kapitoly z matematického modelování |
Výstupy z výukové jednotky |
Obyčejná diferenciální rovnice prvního řádu |
Základní pojmy |
Systémy diferenciálních rovnic a rovnice vyššího řádu |
Elementární metody řešení |
Výstupy z výukové jednotky |
Metoda přímé integrace |
Rovnice se separovanými proměnnými |
Homogenní rovnice |
Lineární rovnice |
Bernoulliova rovnice |
Další metody řešení vybraných typů obyčejných diferenciálních rovnic |
Obecné vlastnosti obyčejných diferenciálních rovnic |
Výstupy z výukové jednotky |
Existence a jednoznačnost řešení systému ODR |
Picardova metoda postupných aproximací |
Globální vlastnosti řešení systému ODR |
Odhady řešení |
Lineární rovnice |
Výstupy z výukové jednotky |
Systémy lineárních ODR |
Princip superpozice |
Metoda variace konstant |
Homogenní lineární systém s konstantní maticí |
Laplaceova transformace |
Řešení počátečního problému metodou postupných aproximací |
Obecné řešení |
Metoda vlastních vektorů |
Úlohy k procvičení |
Lineární diferenciální rovnice vyššího řádu |
Metoda variace konstant |
Převedení systému lineárních diferenciálních rovnic na rovnici vyššího řádu |
Nalezení fundamentálního systému řešení rovnice druhého řádu v případě, že jedno řešení je zn |
Úlohy k procvičení |
Lineární rovnice s konstantními koeficienty |
Homogenní lineární rovnice s konstantními koeficienty |
Partikulární řešení nehomogenní lineární rovnice s konstantními koeficienty a se speciální prav |
Úlohy k procvičení |
Eulerova a Riccatiho diferenciální rovnice |
Výstupy z výukové jednotky |
Laplaceova transformace |
Základní vlastnosti Laplaceovy transformace |
Užití Laplaceovy transformace na řešení diferenciálních rovnic |
Autonomní systémy a kvalitativní teorie |
Výstupy z výukové jednotky |
Autonomní systémy |
Autonomní systémy v rovině |
Autonomní systémy v rovině 2 |
Stabilita |
Přímá Ljapunovova metoda |
Konzervativní systémy |
Některé klasické úlohy |
Výstupy z výukové jednotky |
Traktrisa |
Ciolkovského rovnice |
Archimédova úloha |
Romeo a Julie |
Psí křivka |
Nerelativistický model nestacionárního Vesmíru |
Epidemiologický model Daniela Bernoulliho |
Základní modely populační dynamiky |
Výstupy z výukové jednotky |
Malthusovský model růstu populace |
Verhulstův model růstu populace |
Další modely růstu populace |
Lotkovy-Volterrovy systémy |
Richardsova rovnice |
Smithova rovnice |
Gompertzova rovnice |
Model růstu kulovitých bakterií |
Udržitelný rybolov |
Alleeho efekt |
Rybolov s konstantním úlovkem za jednotku času |
Rybolov s konstantním úsilím |
Optimalizace udržitelného rybolovu |
Úlohy k procvičení |
Výstupy z výukové jednotky |
Lotkovy-Volterrovy systémy |
Obecné vlastnosti Lotkových-Volterrových systémů |
Koloběh dusíku v planktonu |
Trofický řetězec |
Epidemiologické modely |
Biochemické modely |
Výstupy z výukové jednotky |
Základy chemické kinetiky |
Základní modely enzymatické kinetiky |
Biochemické přepínače |
Chemické oscilace |
Reálné biochemické děje |
Dynamika excitabilních systémů |
Výstupy z výukové jednotky |
Přenos signálu v neuronu |
FitzHughův-Nagumův model neuronu |
Hodgkinův-Huxleyho model neuronu |
Šíření vln v excitabilních systémech |
Evoluční dynamika a vývoj vzorců chování |
Výstupy z výukové jednotky |
Základní pojmy teorie her |
Evoluční hry a model jestřáb-holubice |
Replikátorové rovnice |
Literatura |
Rovnice se separovanými proměnnými
Rovnice typu
Tuto rovnici můžeme pomocí diferenciálů zapsat ve tvaru
Za předpokladu 
můžeme rovnici formálně přepsat na tvar
a po integraci obou stran dostaneme
Touto rovností je implicitně zadáno nějaké řešení dané rovnice.
Rovností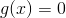 
je implicitně zadáno singulární (konstantní) řešení. Poznamenejme, že singulární řešení může, ale nemusí, být zahrnuto v řešení Elementární metody řešení (1) pro nějakou volbu integrační konstanty. Pokud je singulární řešení zahrnuto ve formuli Elementární metody řešení (1), pak je rovností Elementární metody řešení (1) implicitně zadáno obecné řešení dané rovnice.
Rovností
je implicitně zadáno partikulární řešení dané rovnice, které splňuje počáteční podmínku Obyčejné diferenciální rovnice (2) takovou, že 
. Pokud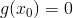 
, pak řešením dané rovnice s počáteční podmínkou Obyčejné diferenciální rovnice (2)
je konstantní funkce 
Povšimněme si, že rovnici typu 1 bez hledané funkce na pravé straně lze považovat za
zvláštní případ rovnice se separovanými proměnnými pro 
. Jiným speciálním případem rovnice se separovanými proměnnými je rovnice autonómní
pro 
