Hodgkinův-Huxleyho model neuronu
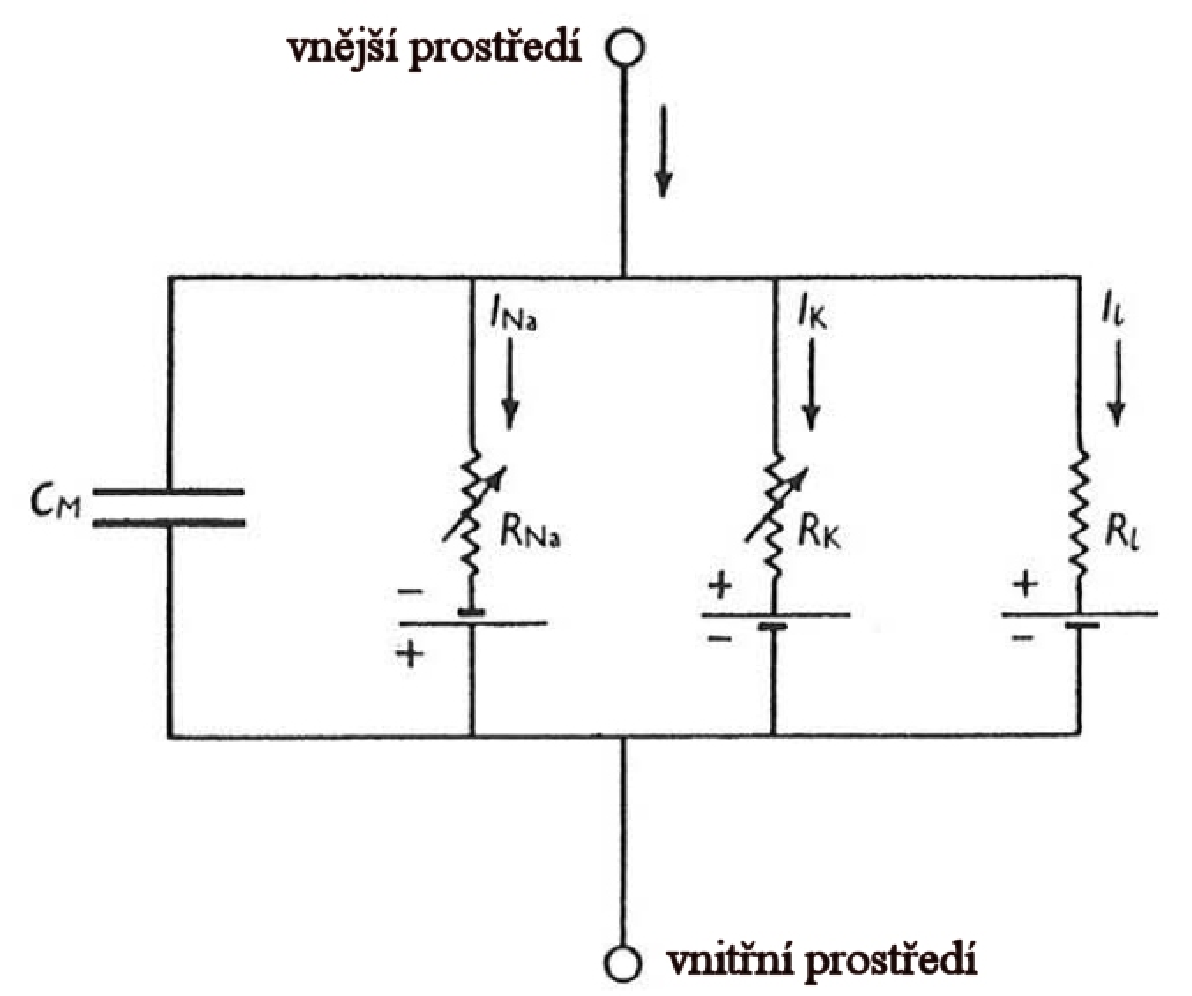
Jak už bylo řečeno, Hodgkinův-Huxleyho model neuronu sestává ze 4 diferenciálních rovnic. První rovnice je fyzikálním popisem elektrického obvodu zobrazeného na následujícim obrázku, představujícího membránu neuronu.
 |
Obr.6. Elektrický obvod reprezentující membránu neuronu. Iontové kanálky mají odpor   a  převrácená hodnota odporu g je elektrická vodivost, která vystupuje jako parametr v Hodgkinově-Huxleyho modelu.
|
Proud procházející obvodem můžeme totiž popsat následující rovnicí
kde 
je napětí na membráně neuronu, 
je kapacita membrány a 
je vnější proud. Jednotlivé členy pravé strany představují proud procházející jednotlivými iontovými kanálky (Na+, K+, Cl-), které jsou dány elektrickou vodivostí vynásobenou převisem napětí (jistě si ze školy pamatujete vzorec 
). Kanálky mají jisté klidové zbytkové napětí, proto zde vystupuje rozdíl tohoto napětí od membránového napětí v obvodu. Odpor 
resp. elektrická vodivost 
iontových kanálků závisí na propustnosti kanálků, zda jsou ochotny propustit ionty nebo ne. Tato závislost byla odhadnuta experimentálně, pro sodíkový iont je to 
pro draslíkový iont je to 
Tuto propustnost či aktivaci jednotlivých kanálků popisují tedy tři další proměnné, které jsou proměnnými závislými na napětí s hodnotami v intervalu 
Funkce aktivace a deaktivace kanálků byly navrženy a odhadnuty na základě experimentů, zde uvedeme jejich typické tvary:
Typické hodnoty vodivostí a zbytkového napětí pro jednotlivé kanálky jsou: 
Hodgkinův-Huxleyho model neuronu je tedy 4-rozměrný systém diferenciálních rovnic Dynamika excitabilních systémů (3), Dynamika excitabilních systémů (4), které splňují experimentálně získané funkční vztahy Dynamika excitabilních systémů (5). Je zřejmé, že počátek není rovnovážným stavem tohoto systému. Pokud bychom ponechali nulový vnější proud 
můžeme numericky získat stabilní rovnováhu
 |
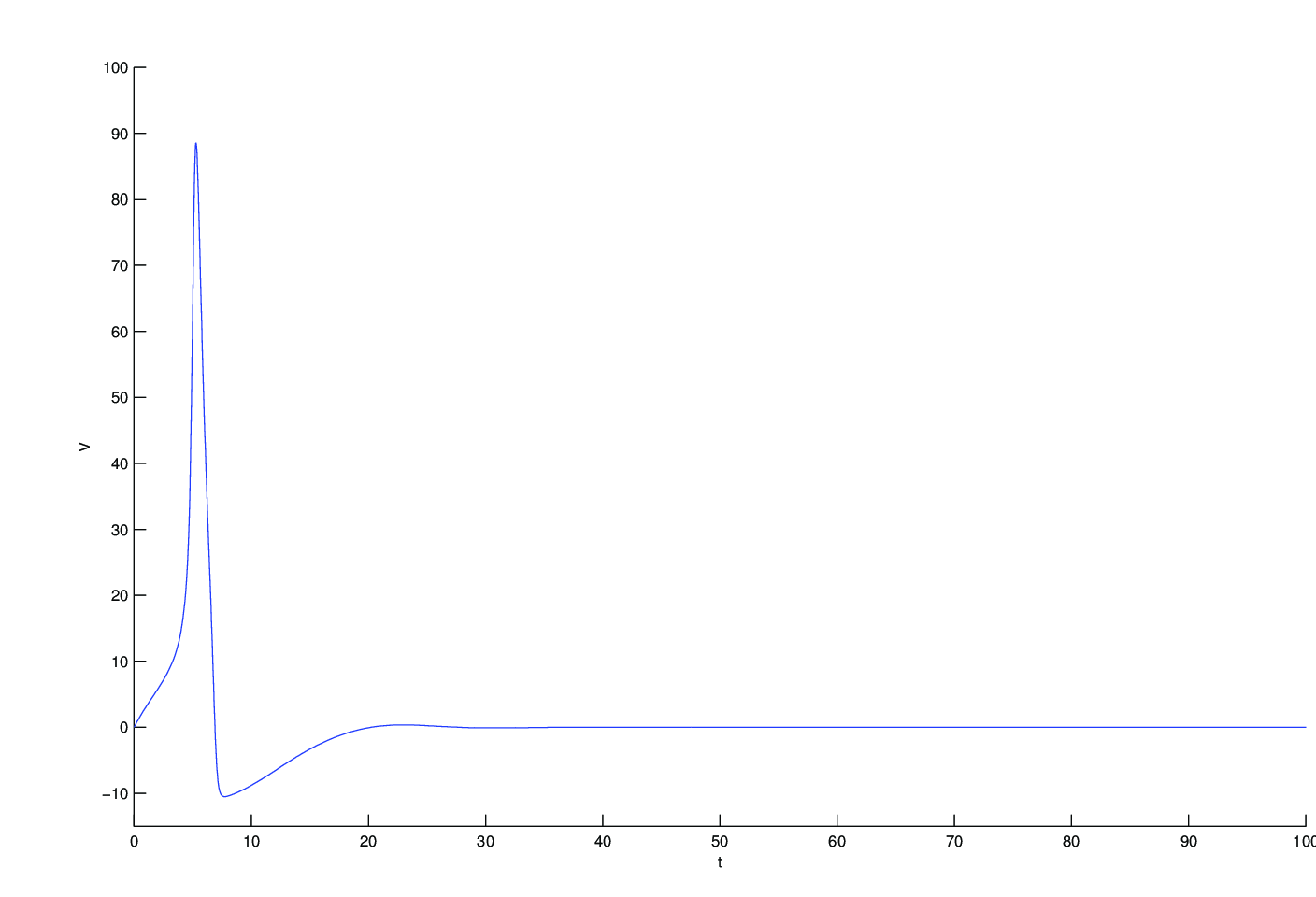
Obr. 7. Vzruch vyvolaný nerovnováhou na membráně, deaktivací iontových kanálků. Pokud bychom sledovali řešení systému Dynamika excitabilních systémů (3), Dynamika excitabilních systémů (4) pro aktivované iontové kanálky  žádný vzruch by nevznikl ani při vyšším napětí na membráně, např. 6 mV. Při počáteční hodnotě napětí 7 mV však už k vzruchu dojde. Chování je podobné redukovanému FitzHughově-Nagumově modelu.
|
