kde představuje prostorovou proměnnou (u axonu nebo dendritu ji můžeme považovat za jednorozměrnou) a je funkce popisující změnu napětí podobně jako to bylo v předchozích modelech. Jde o parciální diferenciální rovnici, tzv. reakčně-difúzní rovnici, kde první člen pravé strany rovnice odpovídá difúzi (šíření akčního potenciálu po dendritu) a druhý člen odpovídá reakci, tedy změně napětí na membráně buňky. Jde vlastně o popis elektrického kabelu, jednotlivých excitabilních buněk seřazených do jednoho spojeného elektrického obvodu. Reakčně-difúzní rovnice vykazují velmi zajímavé a komplexní chování, umožňují například vznik vln, ale také uspořádaných struktur nebo chaotických (nepředvídatelných či nahodilých) dějů. Pro co nejjvětší jednoduchost se pokusíme vysvětlit alespoň vznik vln v kabelové rovnici.

Řešení rovnice Dynamika excitabilních systémů (6) budeme hledat ve tvaru postupující vlny, tj. ve tvaru

kde Jde o transformaci, která posunuje rychlostí ve směru osy Pokud bychom tedy našli nějaké řešení rovnice Dynamika excitabilních systémů (6), ve skutečnosti by šlo o řešení posouvající se rychlostí po ose Takové řešení se nazývá postupující vlnou (travelling wave), která postupuje konstantní rychlostí v jinak neměnném tvaru po ose Pro excitabilní systémy jsou podstatné dva základní typy takových postupujících vln. Jsou to tzv. postupující pulsy, kdy má vlna na počátku a na konci stejnou hodnotu (viz následující obrázek),

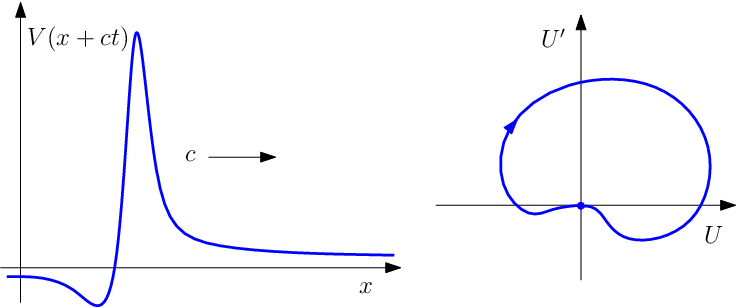Obr.8. Postupující puls.

a druhým typem jsou postupující čela vln, kdy vlna na počátku a na konci nemá stejnou hodnotu (následující obrázek).

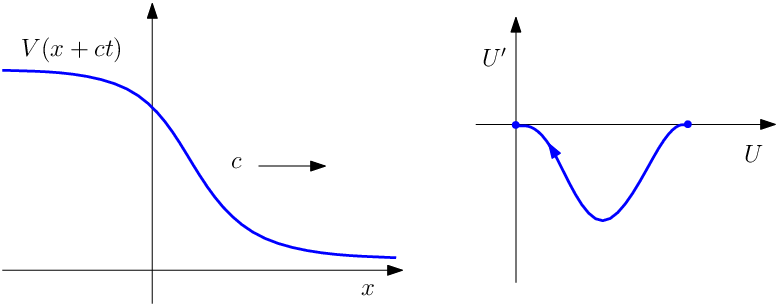Obr. 9. Postupující čelo.

Je zřejmé, že postupujícím pulsem je např. po dendritu se šířící vzruch, vlnou s postupujícím čelem je např. postupné zvýšení akčního potenciálu na membráně axonu či dendritu. Postupujímu pulsu odpovídá trajektorie spojující tentýž rovnovážný bod (tzv. homoklinická trajektorie), postupující vlně pak odpovídá trajektorie spojující různé rovnovážné body (tzv. heteroklinická trajektorie), což si ukážeme v následujícím příkladu.

Příklad. Uveďme nejjednodušší příklad postupujícího čela vlny pro kubickou funkci z FitzHugova-Nagumova modelu ve tvaru

(7)

kde je koeficient difúze a je akční membránový potenciál. Pro jednoduchost uvažujeme nekonečně tenký dendrit, přenos signálu po přímce, tj. V rovnici by samozřejmě měla být obnovovací proměnná jde však o pomalou proměnnou a budeme v tomto okamžiku považovat tuto proměnnou za rovnovážnou.

Označme Transformace převádí rovnici Dynamika excitabilních systémů (7) do tvaru

(8)

kde Zavedením dostáváme dvojrozměrný systém

(9)

Stacionárními body pak budou zřejmě body a Jacobiho matice v těchto bodech je

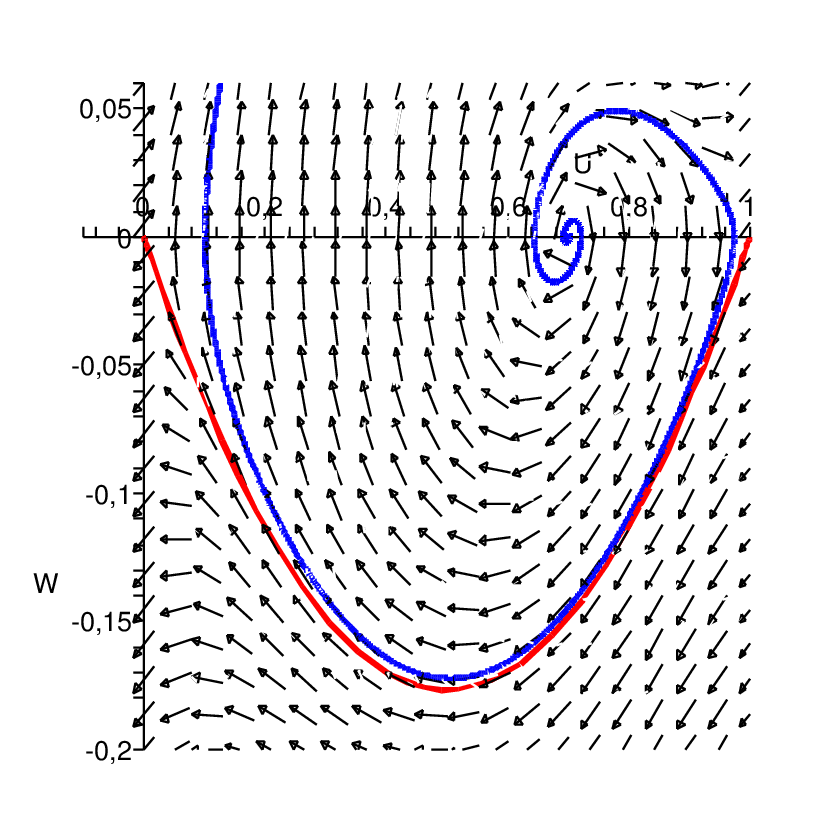
a pro body a platí, že její determinant je záporný (proč?) a jsou to tedy sedla. Fázový portrét na následujícím obrázku ukazuje, že pro jistou vhodnou rychlost jsou sedla spojena jedinou trajektorií (tzv. heteroklinickou trajektorií), jejíž a -limitními množinami jsou právě uvedené body. Pro jiné hodnoty tomu tak není.

Obr. 10. Fázový portrét rovnice Dynamika excitabilních systémů (9) s heteroklinickou trajektorií (červeně) pro D=1 a a=0,7.

Tato trajektorie pro představuje spojnici mezi rovnováhami a a jde tedy o čelo vlny. Pokusíme se najít tuto hodnotu pro kterou jsou sedla spojena heteroklinickou trajektorií odpovídající čelu vlny, tedy rychlost a směr postupu signálu axonem. Protože heterokliniká trajektorie v prostoru spojuje body a budeme předpokládát, že je tvaru

Protože platí a dosazením do Dynamika excitabilních systémů (8) dostáváme, že

a dosazením předpokládaného tvaru pak

Porovnáním koeficientů pak nalezneme hodnotu a Navíc můžeme řešení nalézt separací proměnných z rovnice tj.

Pro všechna záporná platí

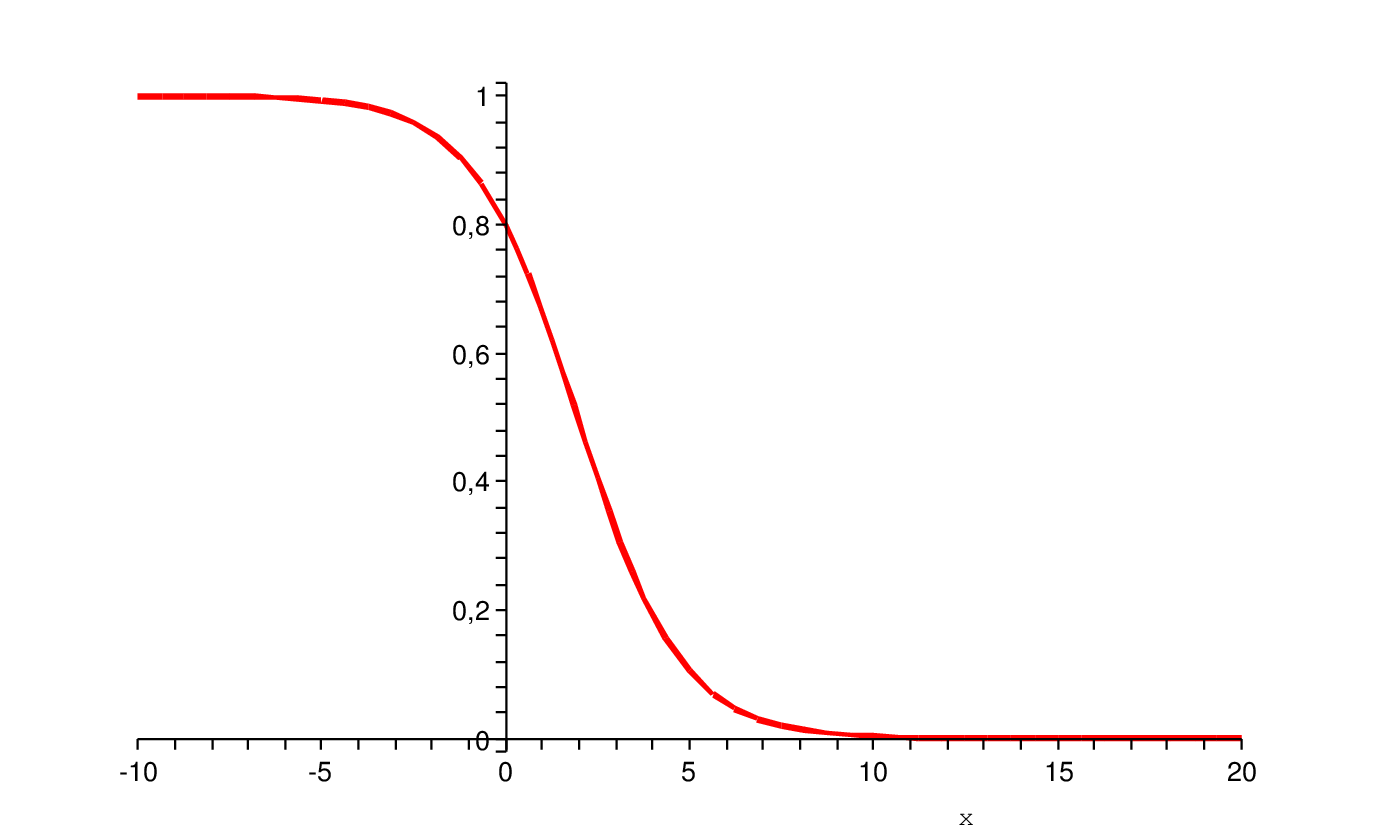
a je klesající spojitá funkce na Různá odpovídají různým počátečním podmínkách času a místa (). Následující brázek ukazuje pro

Obr. 11. Postupující vlna.

Toto řešení nezávisí na ale posun této čelní vlny je s svázán. Pro je a v daném místě se bude hodnota akčního potenciálu zvyšovat, v opačném případě snižovat.

Úlohy k procvičení

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity