Standardizované normální rozdělení
Mezi výhodné vlastnosti normálního rozdělení patří zachování normality při změně měřítka osy, na které měříme jednotky náhodné veličiny X. Jinými slovy, pokud veličinu X s rozdělením N(µ,σ2) transformujeme podle vztahu Y = a + bX, pak platí, že náhodná veličina Y má rozdělení pravděpodobnosti N(a + bµ, b2σ2). S využitím této vlastnosti jsme vždy schopni transformovat náhodnou veličinu X s rozdělením N(µ,σ2) na náhodnou veličinu Z s rozdělením N(0,1), tedy s normálním rozdělením s nulovou střední hodnotou a jednotkovým rozptylem. Platí
|
|
(4.12) |
Toto rozdělení má ve statistice výsadní postavení a označuje se jako standardizované normální rozdělení (standard normal distribution). Jeho hustota pak má následující tvar:
|
|
(4.13) |
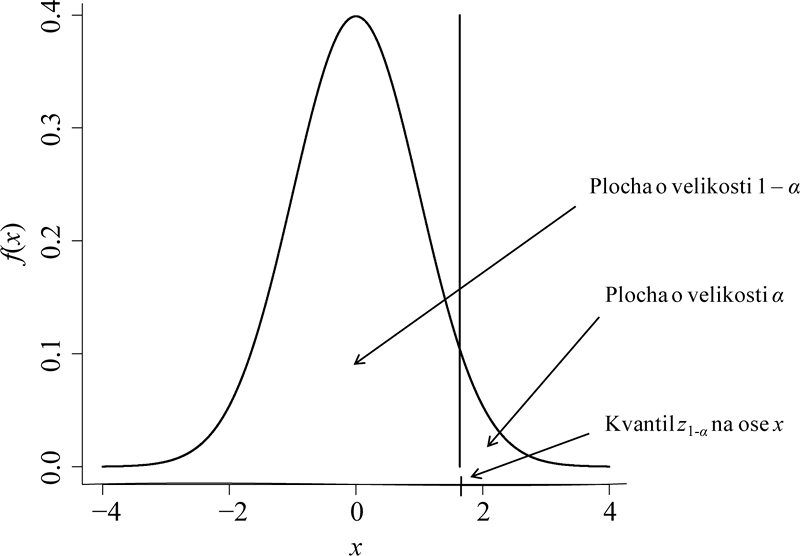
Výhoda je, že všechny hodnoty distribuční i kvantilové funkce jsou tabelovány a obsaženy v dostupných softwarech (kvantily standardizovaného normálního rozdělení se označují jako z). Můžeme tak jednoduše kvantifikovat pravděpodobnost, s jakou se náhodná veličina Z se standardizovaným normálním rozdělením realizuje nad určitou hodnotou z (případně pod ní, nebo mezi dvěma danými hodnotami). Obecně lze plochu pod hustotou rozdělit pomocí kvantilu na dvě části, např. pomocí 100(1 – α)procentního kvantilu, označme ho z1-α, na část s plochou 1 – α a na část s plochou α (viz obrázek 4.2). Toto dělení samozřejmě odpovídá pravděpodobnosti, tedy náhodná veličina Z se realizuje číslem menším než z1-α s pravděpodobností 1 – α a číslem větším než z1-α s pravděpodobností α.
Příklad 4.2. Při populačním epidemiologickém průzkumu se zjistilo, že průměrný objem prostaty u mužů (veličina X) je 52,73 ml se směrodatnou odchylkou rovnou 13,12 ml. Předpokládáme, že objem prostaty se řídí normálním rozdělením, za hodnoty parametrů µ a σ2 bereme populační odhady. Zajímá nás, jaká je pravděpodobnost, že objem prostaty u muže bude větší než 80 ml. Abychom zjistili, jaká pravděpodobnost přísluší hodnotě 80 ml jako kvantilu rozdělení náhodné veličiny X, provedeme standardizaci a zjistíme příslušnou pravděpodobnost na základě kvantilu standardizované normální veličiny Z. Výpočet hodnoty veličiny Z je následující:
|
|
(4.14) |
Víme, že hodnota 2,08 představuje 100(1 – α)procentní kvantil, z1-α, standardizované normální veličiny Z, k ní odpovídající hladinu α zjistíme z tabulek hodnot kvantilové funkce. Lze zjistit, že pravděpodobnost výskytu hodnoty větší než 2,08 je pro standardizovanou normální veličinu rovna 0,0188, což tedy znamená, že pravděpodobnost výskytu prostaty s objemem větším než 80 ml je rovna přibližně 2%.
Obr. 4.2: Plochy pod hustotou pravděpodobnosti příslušné kvantilu z1-α.
Oblast, kde se náhodná veličina Z se standardizovaným normálním rozdělením realizuje s pravděpodobností 1 – α lze vyjádřit pomocí její distribuční funkce (ta vyjadřuje pravděpodobnost, že číselná realizace náhodné veličiny nepřekročí na reálné ose danou hodnotu) a příslušných kvantilů následujícím způsobem:
|
|
(4.15) |
Jinými slovy, oblast realizace náhodné veličiny Z s rozdělením N(0,1) odpovídající pravděpodobnosti 1 – α lze vymezit pomocí jejích kvantilů, jmenovitě pomocí 100(α/2)procentního kvantilu, zα/2, a 100(1 – α/2)procentního kvantilu, z1-α/2. Vzhledem k symetrii hustoty standardizovaného normálního rozdělení jsou vždy tyto dva kvantily identické až na znaménko, tedy platí z1-α/2 = – zα/2.
Klíčové kvantily standardizovaného normálního rozdělení uvádí obrázek 4.3, ze kterého vyplývá, že náhodná veličina s rozdělením N(0,1) se s pravděpodobností 90% realizuje mezi hodnotou -1,64 a hodnotou 1,64, s pravděpodobností 95% mezi hodnotami -1,96 a 1,96 a s pravděpodobností 99% nepřekročí v absolutní hodnotě číslo 2,58.
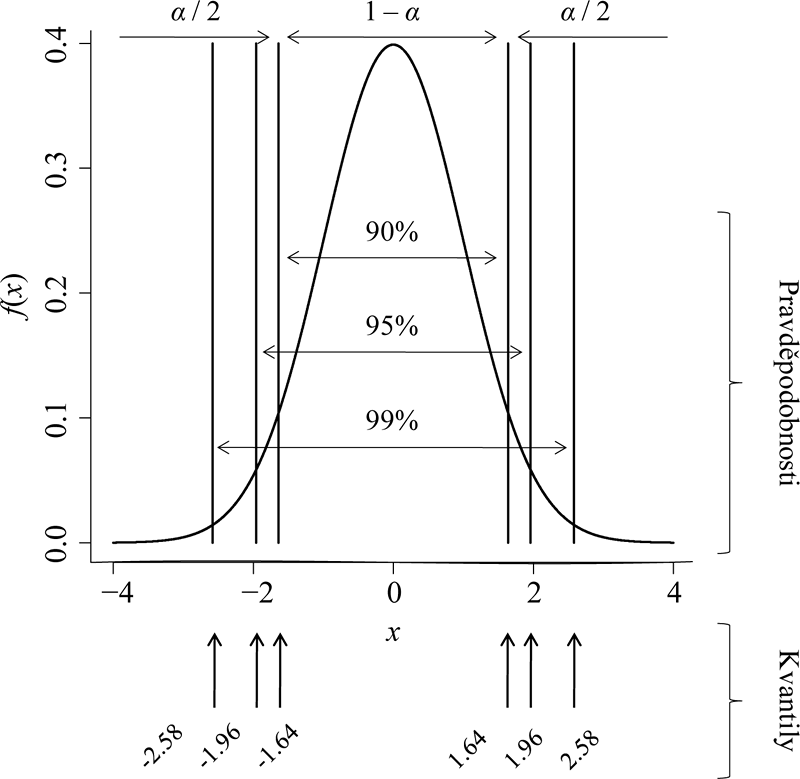
Obr. 4.3: Klíčové kvantily standardizovaného normálního rozdělení pravděpodobnosti.
Vymezení oblasti, kde se náhodná veličina realizuje s určitou pravděpodobností je platné pro všechna rozdělení pravděpodobnosti, nejen pro standardizované normální (i když u rozdělení N(0,1) se vzhledem k jeho symetrii významné kvantily dobře pamatují). Tento fakt je velmi důležitý zejména v testování hypotéz, kde na základě toho, v jaké oblasti se realizuje hodnota testové statistiky (náhodné veličiny s daným rozdělením pravděpodobnosti), rozhodujeme o platnosti nebo neplatnosti sledované hypotézy.